Bezwzględne odchylenie średnie a odchylenie standardowe: jaka jest różnica?
Odchylenie standardowe jest jednym z najpowszechniejszych sposobów pomiaru rozproszenia zbioru danych.
Oblicza się go w następujący sposób:
Odchylenie standardowe = √( Σ(x i – x ) 2 / n )
Innym sposobem pomiaru rozkładu obserwacji w zbiorze danych jest średnie odchylenie bezwzględne .
Oblicza się go w następujący sposób:
Średnie odchylenie bezwzględne = Σ|x i – x | /nie
W tym samouczku wyjaśniono różnice między tymi dwoma metrykami wraz z przykładami obliczania każdej z nich.
Podobieństwa i różnice
Jak sama nazwa wskazuje, odchylenie standardowe i średnie odchylenie bezwzględne próbują określić ilościowo typowe odchylenie obserwacji od średniej w danym zbiorze danych.
Jednak metoda stosowana w przypadku każdego miernika jest inna.
Odchylenie standardowe
Odchylenie standardowe pozwala znaleźć kwadratową różnicę między każdą obserwacją a średnią zbioru danych. Następnie uśrednia te kwadraty różnic i wyciąga pierwiastek kwadratowy.
W ten sposób otrzymujemy liczbę reprezentującą „standard” lub typowe odchylenie obserwacji od średniej.
Oznacza odchylenie absolutne
I odwrotnie, średnie odchylenie bezwzględne pozwala znaleźć bezwzględne odchylenie między każdą obserwacją a średnią zbioru danych. Następnie znajduje średnią z tych odchyleń.
W ten sposób otrzymujemy liczbę reprezentującą średnie odchylenie obserwacji od średniej.
Ponieważ odchylenie standardowe pozwala znaleźć kwadraty różnic, zawsze będzie równe lub większe od średniego odchylenia bezwzględnego.
W przypadku występowania skrajnych wartości odstających odchylenie standardowe będzie znacznie większe niż średnie odchylenie bezwzględne. Poniższy przykład ilustruje tę kwestię.
Przykład: średnie bezwzględne odchylenie od odchylenia standardowego
Załóżmy, że mamy następujący zestaw danych składający się z 8 wartości:
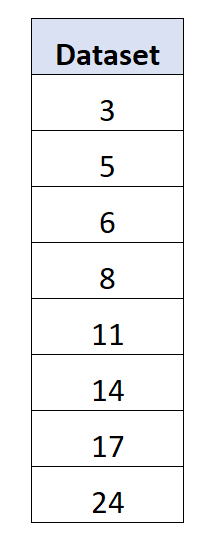
Średnia wynosi 11 .
Zatem średnie odchylenie bezwzględne obliczylibyśmy w następujący sposób:
Średnie odchylenie bezwzględne = (|3-11| + |5-11| + |6-11| + |8-11| + |11-11| + |14-11| + |17-11| + |24- 11|) / 8 = 5,5 .
Obliczylibyśmy odchylenie standardowe w następujący sposób:
Odchylenie standardowe = √((3-11) 2 + (5-11) 2 + (6-11) 2 + (8-11) 2 + (11-11) 2 + (14-11) 2 + (17- 11) 2 + (24-11) 2 )/8) = 6,595 .
Jak wspomniano wcześniej, odchylenie standardowe będzie zawsze równe lub większe od średniego odchylenia bezwzględnego.
Jednakże różnica między odchyleniem standardowym a średnim odchyleniem bezwzględnym będzie szczególnie duża, jeśli w zbiorze danych występują skrajne wartości odstające.
Rozważmy na przykład następujący zbiór danych ze skrajną wartością odstającą dla ostatniej wartości:
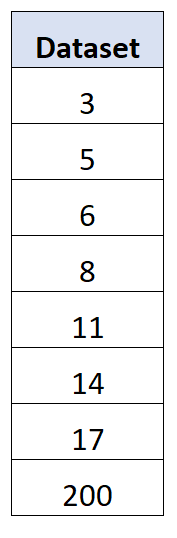
Okazuje się, że odchylenie standardowe dla tego zbioru danych wynosi 63,27 , podczas gdy średnie odchylenie bezwzględne wynosi 41,75 .
Skrajna wartość odstająca powoduje, że odchylenie standardowe jest znacznie większe niż średnie odchylenie bezwzględne.