Średnia ważona

Przez Benjamin Anderson 6 sierpnia, 2023 Statystyka 0 komentarzy

Tutaj wyjaśniamy, czym jest średnia ważona i jak jest obliczana. Będziesz mógł zobaczyć rozwiązane ćwiczenie dotyczące znajdowania średniej ważonej. Co więcej, za pomocą kalkulatora na końcu możesz obliczyć średnią ważoną dowolnego zestawu danych.

Jaka jest średnia ważona?

Średnia ważona jest miarą centralności statystyki opisowej. Aby obliczyć średnią ważoną, należy najpierw pomnożyć każdą dane statystyczną przez jej wagę (lub wagę), następnie dodać wszystkie iloczyny, a na koniec podzielić sumę ważoną przez sumę wszystkich wag.

Innymi słowy, wzór na średnią ważoną jest następujący:

Gdzie x _i reprezentuje każdą próbkę danych, a w _i odpowiadającą jej wagę.

Zatem im większą wagę mają dane, tym ważniejsze stają się one przy obliczaniu średniej ważonej. Innymi słowy, im większa waga fragmentu danych, tym większy będzie to miało wpływ na wynik średniej ważonej.

Średnia ważona jest szczególnie przydatna do obliczania ocen, ponieważ pozwala na ocenę z różną wagą ćwiczeń lub egzaminów zdanych w trakcie zajęć. Średnia ważona jest również wykorzystywana do obliczania CPI (wskaźnika cen towarów i usług konsumenckich), który jest wskaźnikiem służącym do pomiaru cen w populacji.

Oprócz średniej ważonej istnieją również inne rodzaje średnich, takie jak średnia geometryczna, średnia arytmetyczna, średnia kwadratowa i średnia harmoniczna.

Jak obliczyć średnią ważoną

Aby obliczyć średnią ważoną, należy wykonać następujące kroki:

Pomnóż każde dane statystyczne przez odpowiednią wagę.
Zsumuj wszystkie produkty obliczone w poprzednim kroku.
Podziel sumę ważoną powyżej przez sumę wszystkich wag.
Otrzymany wynik jest średnią ważoną próby statystycznej.

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć średnią ważoną dowolnego zbioru danych.

Przykład średniej ważonej

Biorąc pod uwagę definicję średniej ważonej, rozwiążemy teraz ćwiczenie, aby w pełni zrozumieć, w jaki sposób uzyskuje się średnią ważoną ze zbioru danych.

Uczeń I klasy liceum uzyskał następujące oceny z przedmiotu matematyka: 7 z egzaminu cząstkowego, co liczy się na 30%, 9 z pracy w grupach, co stanowi 20%, 6 z ćwiczeń wykonywanych na zajęciach z wagą 10% i 8 z egzaminu końcowego, którego waga wynosi 40%. Jaka jest Twoja końcowa ocena z przedmiotu?

Aby ustalić ocenę ucznia, należy znaleźć średnią ważoną z wartościami podanymi w zestawieniu. W tym celu stosujemy wzór na średnią ważoną:

$\overline{x_p}=\cfrac{\sum_{i=1}^N x_i\cdot w_i}{\sum_{i=1}^N w_i}=\cfrac{x_1\cdot w_1+x_2\cdot w_2+x_3\cdot w_3+x_4\cdot w_4+x_5\cdot w_5}{w_1+w_2+w_3+w_4+w_5}$

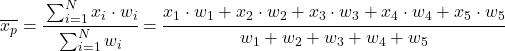
Wynik każdego wyniku jest wartością statystyczną, a jego procent odpowiada wadze tej wartości. Dlatego podstawiamy wartości i wagi do wzoru i wykonujemy obliczenie średniej ważonej:

$\overline{x_p}=\cfrac{7\cdot 0,30+9\cdot 0,20+6\cdot 0,10+8\cdot 0,40}{0,30+0,20+0,10+0,40}=7,7$

Ostateczna ocena z matematyki tego ucznia wyniesie zatem 7,7, ponieważ jest to wynik uzyskany na podstawie średniej ważonej.

Kalkulator średniej ważonej

Wprowadź dane z dowolnej próbki statystycznej i ich odpowiednie wagi do poniższego kalkulatora, aby obliczyć jej średnią ważoną.

Wpisz dane statystyczne w pierwszym polu i odpowiadające im wagi w drugim polu. Wagi należy wpisać w tej samej kolejności co dane i w formacie dziesiętnym. Wszystkie liczby muszą być oddzielone spacją i wprowadzone z użyciem kropki jako separatora dziesiętnego.

Standaryzowane wagi

Jak widzieliśmy, w średniej ważonej waga to wartość nadawana każdemu elementowi danych w celu nadania mu większego lub mniejszego znaczenia. Tak więc, jeśli informacja jest bardzo ważna, będzie miała bardzo dużą wagę, ale jeśli informacja nie jest zbyt istotna, będzie miała bardzo niską wagę.

Cóż, waga znormalizowana to rodzaj ważenia używany do uzyskania średniej ważonej bez konieczności wykonywania jakiegokolwiek dzielenia.

Znormalizowana waga to waga elementu danych podzielona przez sumę wszystkich wag.

$w_i'=\cfrac{w_i}{\sum_{k=1}^N w_k}$

Suma wszystkich znormalizowanych wag jest zatem równa jeden:

$\sum_{i=1}^N w_i'=1$

Aby więc obliczyć średnią ważoną przy użyciu znormalizowanych wag , wystarczy pomnożyć każdy element danych przez jego znormalizowaną wagę:

$\displaystyle\overline{x_p}=\sum_{i=1}^N x_i\cdot w_i'=x_1\cdot w_1'+x_2\cdot w_2'+\dots+x_N\cdot w_N'$

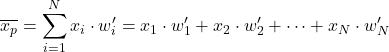
Na przykład mamy próbkę statystyczną, której dane wynoszą 24, 35, 17, 41, a ich odpowiednie wagi to 4, 9, 6, 3. Aby znaleźć średnią ważoną tego zbioru danych, możemy najpierw obliczyć znormalizowane wagi, dzieląc każda waga jako suma wszystkich wag:

$\cfrac{4}{4+9+6+3}=0,18$

$\cfrac{9}{4+9+6+3}=0,41$

$\cfrac{6}{4+9+6+3}=0,27$

$\cfrac{3}{4+9+6+3}=0,14$

A teraz wystarczy pomnożyć każde dane przez ich znormalizowaną wagę, a wynikiem będzie średnia ważona:

$\overline{x_p}=24\cdot 0,18+35\cdot 0,41+17\cdot 0,27+41\cdot 0,14=28,91$

Różnica między średnią ważoną a średnią arytmetyczną

Obliczanie średniej ważonej i średniej arytmetycznej odbywa się w ten sam sposób, ponieważ należy wykonać podobne operacje. W przypadku uśredniania ważonego każdy punkt danych jest mnożony przez jego wagę i dzielony przez sumę wag, natomiast w przypadku uśredniania arytmetycznego wszystkie dane są sumowane i dzielone przez całkowitą liczbę punktów danych.

Różnica między średnią ważoną a średnią arytmetyczną polega na jej koncepcji, ponieważ w średniej arytmetycznej uważa się, że wszystkie dane mają tę samą wartość, natomiast w średniej ważonej każde dane mają inną wagę.

Należy pamiętać, że jeśli wszystkie wagi są równe, średnia ważona jest równa średniej arytmetycznej. Poniżej możesz zobaczyć dowód matematyczny:

$\begin{aligned}\overline{x_p}&=\cfrac{x_1\cdot w+x_2\cdot w+x_3\cdot w+\dots+x_N\cdot w}{w+w+w+\dots +w}\\[2ex]&= \cfrac{w\cdot (x_1+x_2+\dots+x_N)}{N\cdot w}=\\[2ex] &= \cfrac{x_1+x_2+\dots+x_N}{N}=\overline{x}\end{aligned}$

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej