Co to jest łączny rozkład prawdopodobieństwa?
Dwuczynnikowa tabela częstości to tabela, która wyświetla częstości (lub „liczby”) dla dwóch zmiennych kategorycznych.
Na przykład poniższa dwukierunkowa tabela przedstawia wyniki ankiety, w której zapytano 100 osób, jaki sport preferują: baseball, koszykówkę czy piłkę nożną.
W wierszach wyświetlana jest płeć respondenta, a kolumny wskazują wybrany przez niego sport:

W tym przykładzie istnieją dwie zmienne: sport i płeć.
Łączny rozkład prawdopodobieństwa opisuje po prostu prawdopodobieństwo, że dana osoba przyjmie dwie określone wartości dla zmiennych.
Słowo „koniukcja” bierze się z faktu, że interesuje nas prawdopodobieństwo wystąpienia dwóch rzeczy w tym samym czasie.
Na przykład spośród 100 osób 13 było płci męskiej i wybrało baseball jako swój ulubiony sport.
Powiedzielibyśmy więc, że łączne prawdopodobieństwo, że dana osoba jest mężczyzną i wybierze baseball jako swój ulubiony sport, wynosi 13/100 = 0,13 lub 13% .
Zapisane w notacji matematycznej:
P(płeć = mężczyzna, sport = baseball) = 13/100 = 0,13 .
Możemy użyć tego procesu do obliczenia całego łącznego rozkładu prawdopodobieństwa:
- P (płeć = mężczyzna, sport = baseball) = 13/100 = 0,13
- P(płeć = mężczyzna, sport = koszykówka) = 15/100 = 0,15
- P(płeć = mężczyzna, sport = piłka nożna) = 20/100 = 0,20
- P (płeć = kobieta, sport = baseball) = 23/100 = 0,23
- P(płeć = kobieta, sport = koszykówka) = 16/100 = 0,16
- P(płeć = kobieta, sport = piłka nożna) = 13/100 = 0,13
Zauważ, że suma prawdopodobieństw jest równa 1 lub 100% .
Po co stosować łączny rozkład prawdopodobieństwa?
Łączne rozkłady prawdopodobieństwa są przydatne, ponieważ często zbieramy dane dla dwóch zmiennych (takich jak sport i płeć) i chcemy odpowiedzieć na pytania związane z obiema zmiennymi.
Na przykład możemy chcieć zrozumieć prawdopodobieństwo, że dana osoba w populacji jest mężczyzną i preferuje baseball jako swój ulubiony sport.
Możemy też być zainteresowani poznaniem prawdopodobieństwa, że dana osoba jest kobietą i preferuje piłkę nożną jako swój ulubiony sport.
Wspólny rozkład prawdopodobieństwa może pomóc nam odpowiedzieć na te pytania.
Poniższe przykłady wykorzystaj w praktyce, aby lepiej zrozumieć łączne rozkłady prawdopodobieństwa.
Przykład 1
Poniższa dwukierunkowa tabela przedstawia wyniki ankiety, w której zapytano 238 osób, jaki rodzaj filmów preferują:
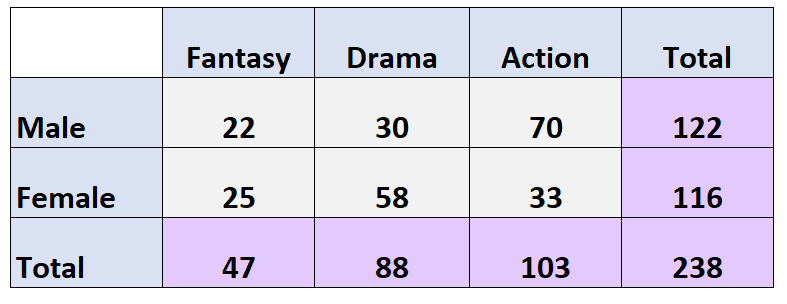
Pytanie: Jakie jest prawdopodobieństwo, że dana osoba jest kobietą i preferuje dramat jako swój ulubiony gatunek filmowy?
Odpowiedź: P (płeć = kobieta, płeć = dramat) = 58/238 = 0,244 = 24,4%
Przykład 2
Poniższa dwukierunkowa tabela przedstawia wyniki egzaminów 64 uczniów w klasie na podstawie liczby godzin spędzonych na nauce:
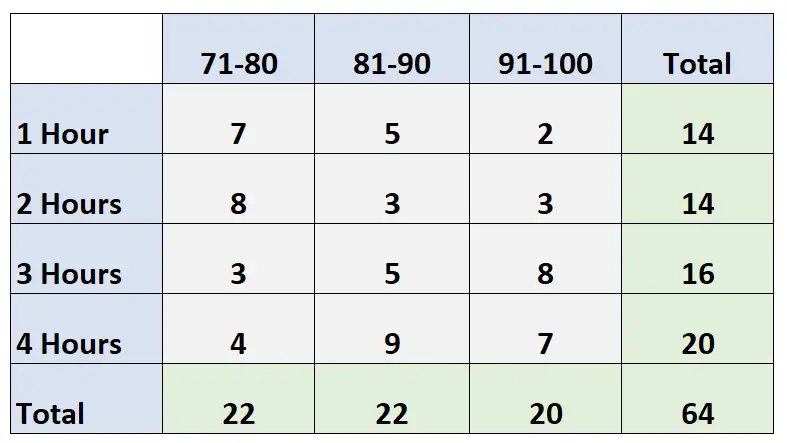
Pytanie: Jakie jest prawdopodobieństwo, że dana osoba będzie uczyć się 2 godziny i otrzyma ocenę pomiędzy 91 a 100?
Odpowiedź: P (badanie = 2 godziny, wynik = 91-100) = 3/64 = 0,047 = 4,7%
Dodatkowe zasoby
Co to jest dystrybucja krańcowa?
Jak znaleźć warunkową częstotliwość względną w tabeli z podwójnym wpisem