Wydarzenia wzajemnie włączające się lub wykluczające

Dwa zdarzenia wykluczają się wzajemnie, jeżeli nie mogą wystąpić jednocześnie.

Załóżmy na przykład, że zdarzenie A to zdarzenie, w którym kość wyląduje na liczbie parzystej, a zdarzenie B to zdarzenie, w którym kość wyląduje na liczbie nieparzystej.

Zdefiniowalibyśmy przykładową przestrzeń dla zdarzeń w następujący sposób:

• ZA = {2, 4, 6}
• B = {1, 3, 5}

Należy zwrócić uwagę, że dwie próbkowane przestrzenie nie nakładają się na siebie. Zatem zdarzenia A i B wykluczają się wzajemnie, ponieważ nie mogą wystąpić jednocześnie. Liczba, na którą wypadnie kość, nie może być jednocześnie parzysta i nieparzysta.

I odwrotnie, dwa zdarzenia wykluczają się wzajemnie , jeśli mogą wystąpić w tym samym czasie.

Na przykład, niech zdarzenie C będzie zdarzeniem, w którym kość wypadnie na liczbę parzystą i niech zdarzenie D będzie zdarzeniem, w którym kość wyląduje na liczbie większej niż 3.

Zdefiniowalibyśmy przykładową przestrzeń dla zdarzeń w następujący sposób:

• C = {2, 4, 6}
• re = {4, 5, 6}

Należy zwrócić uwagę, że dwie próbkowane przestrzenie nakładają się na siebie. Zatem zdarzenia C i D wzajemnie się wykluczają, ponieważ mogą wystąpić w tym samym czasie. Może się zdarzyć, że kostka wyląduje na liczbie parzystej większej niż 3.

Prawdopodobieństwa zdarzeń

Jeżeli dwa zdarzenia wykluczają się wzajemnie , prawdopodobieństwo ich wystąpienia wynosi zero.

Rozważmy na przykład dwie przykładowe przestrzenie dla zdarzeń A i B powyżej:

• ZA = {2, 4, 6}
• B = {1, 3, 5}

Ponieważ przestrzenie próbek nie pokrywają się, powiedzielibyśmy P(A i B) = 0 .

Ale jeśli dwa zdarzenia wzajemnie się wykluczają , wówczas prawdopodobieństwo ich wystąpienia będzie liczbą większą od zera.

Rozważmy na przykład poprzednie dwie przykładowe przestrzenie dla zdarzeń C i D:

• C = {2, 4, 6}
• re = {4, 5, 6}

Ponieważ istnieje 6 możliwych liczb, na których mogą wylądować kości, a dwie z tych liczb (4 i 6) należą do obu zdarzeń C i D, obliczylibyśmy P(C i D) jako 2/6 lub 1/3 .

Przeglądaj wydarzenia wzajemnie włączające i wykluczające się

Często używamy diagramów Venna do wizualizacji prawdopodobieństw związanych ze zdarzeniami.

Jeśli dwa zdarzenia wzajemnie się wykluczają, na diagramie Venna w ogóle nie będą się nakładać:

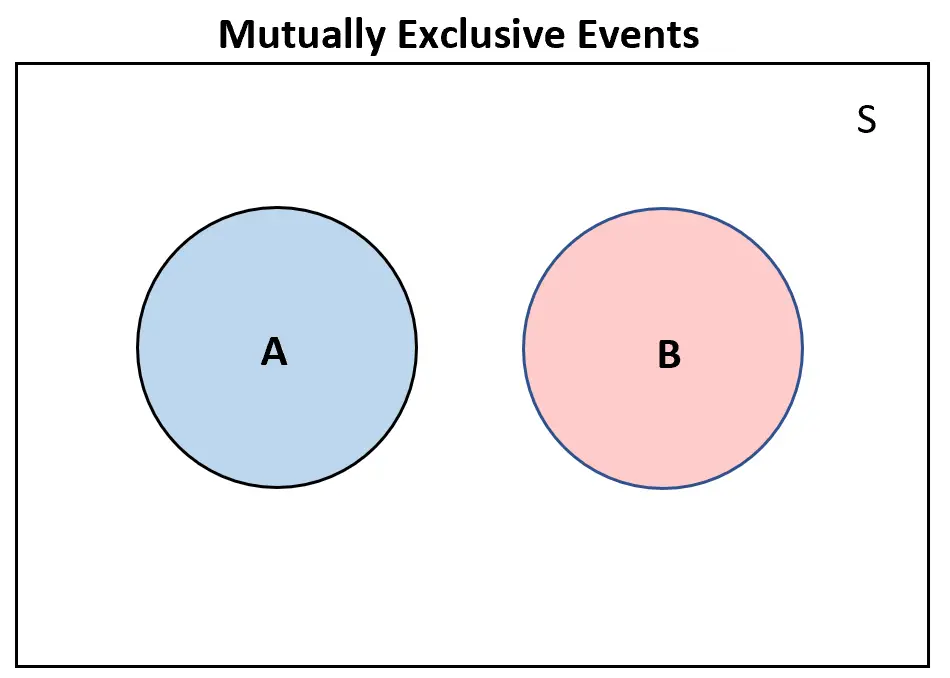
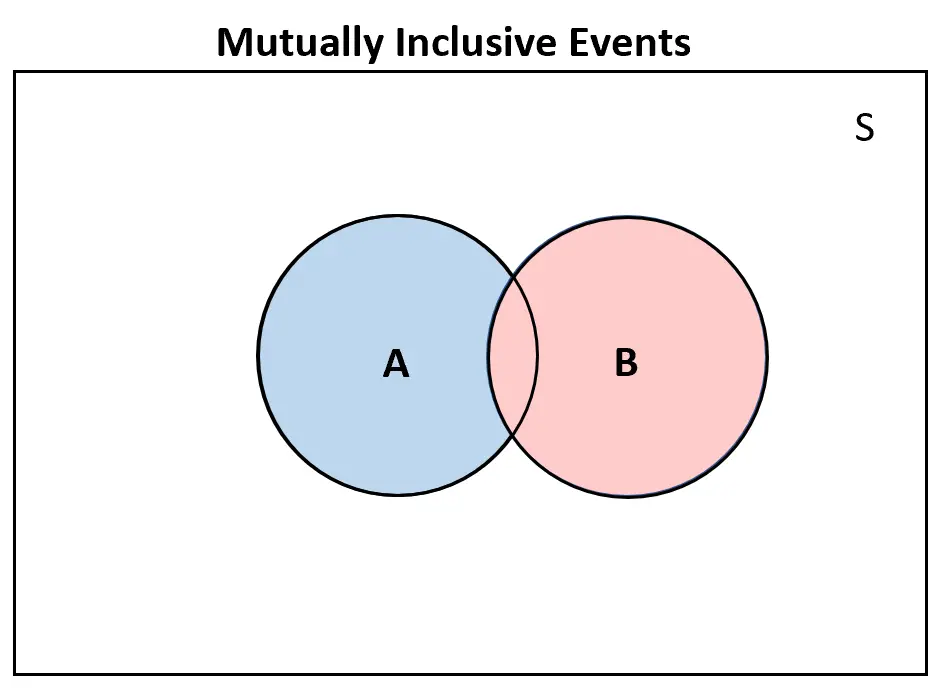
I odwrotnie, jeśli dwa zdarzenia wzajemnie się wykluczają , na diagramie Venna będzie przynajmniej w pewnym stopniu nakładać się:

Dodatkowe zasoby

Wprowadzenie do prawdopodobieństwa teoretycznego
Ogólna zasada mnożenia
Co to są zdarzenia rozłączne?