Test breuscha-pagana: definicja i przykład

Jednym z kluczowych założeń regresji liniowej jest to, że reszty mają rozkład z równą wariancją na każdym poziomie zmiennej predykcyjnej. Założenie to znane jest jako homoskedastyczność .

Jeżeli to założenie nie jest przestrzegane, mówi się, że w resztach występuje heteroskedastyczność . Kiedy tak się dzieje, wyniki regresji stają się niewiarygodne.

Jednym ze sposobów wizualnego wykrycia obecności heteroskedastyczności jest utworzenie wykresu reszt względem dopasowanych wartości z modelu regresji.

Jeśli reszty rozkładają się bardziej przy wyższych wartościach na wykresie, jest to charakterystyczny znak obecności heteroskedastyczności.

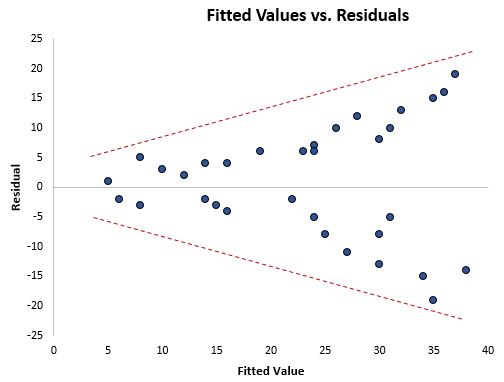
Formalnym testem statystycznym, którego możemy użyć do określenia, czy występuje heteroskedastyczność, jest test Breuscha-Pagana .

Ten samouczek zawiera krótkie wyjaśnienie testu Breuscha-Pagana wraz z przykładem.

Co to jest test Breuscha-Pagana?

Test Breuscha-Pagana służy do określenia, czy w modelu regresji występuje heteroskedastyczność.

W teście wykorzystuje się następujące hipotezy zerowe i alternatywne:

• Hipoteza zerowa (H ₀ ): występuje homoskedastyczność (reszty rozkładają się z równą wariancją)
• Hipoteza alternatywna ( _HA ): występuje heteroskedastyczność (reszty nie są rozłożone z równą wariancją)

Jeśli wartość p testu jest poniżej pewnego poziomu istotności (tj. α = 0,05), wówczas odrzucamy hipotezę zerową i stwierdzamy, że w modelu regresji występuje heteroskedastyczność.

Aby wykonać test Breuscha-Pagana, stosujemy następujące kroki:

1. Dopasuj model regresji.

2. Oblicz kwadraty reszt modelu.

3. Dopasuj nowy model regresji, używając kwadratów reszt jako wartości odpowiedzi.

4. Oblicz statystykę testową Chi-kwadrat X ² w postaci n*R ² _new gdzie:

• n: Całkowita liczba obserwacji
• R ² _nowość : R kwadrat nowego modelu regresji, w którym jako wartości odpowiedzi wykorzystano kwadraty reszt

Jeśli wartość p odpowiadająca tej statystyce testu chi-kwadrat z p (liczbą predyktorów) stopni swobody jest poniżej pewnego poziomu istotności (tj. α = 0,05), wówczas odrzuć hipotezę zerową i wyciągnij wniosek, że występuje heteroskedastyczność .

W przeciwnym razie nie odrzucaj hipotezy zerowej. W tym przypadku zakłada się, że występuje homoskedastyczność.

Należy pamiętać, że większość programów statystycznych może z łatwością przeprowadzić test Breuscha-Pagana, więc prawdopodobnie nigdy nie będziesz musiał wykonywać tych kroków ręcznie, ale warto wiedzieć, co dzieje się za kulisami.

Przykład testu Breuscha-Pagana

Załóżmy, że mamy następujący zbiór danych zawierający informacje o 10 różnych koszykarzach:

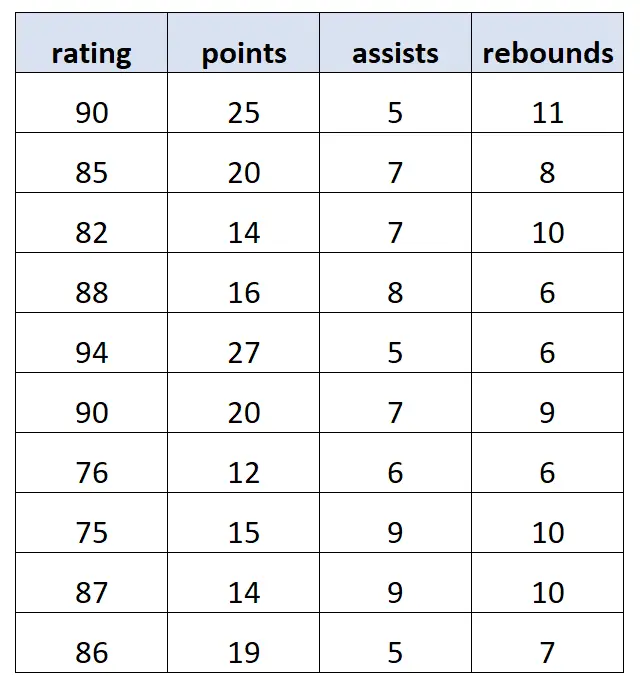
Korzystając z oprogramowania statystycznego, dopasowujemy następujący model regresji liniowej wielokrotnej :

wynik = 62,47 + 1,12*(punkty) + 0,88*(asysty) – 0,43*(zbiórki)

Następnie używamy tego modelu, aby przewidzieć ocenę każdego gracza i obliczyć kwadraty reszt (tj. kwadratową różnicę między przewidywaną oceną a rzeczywistą oceną):

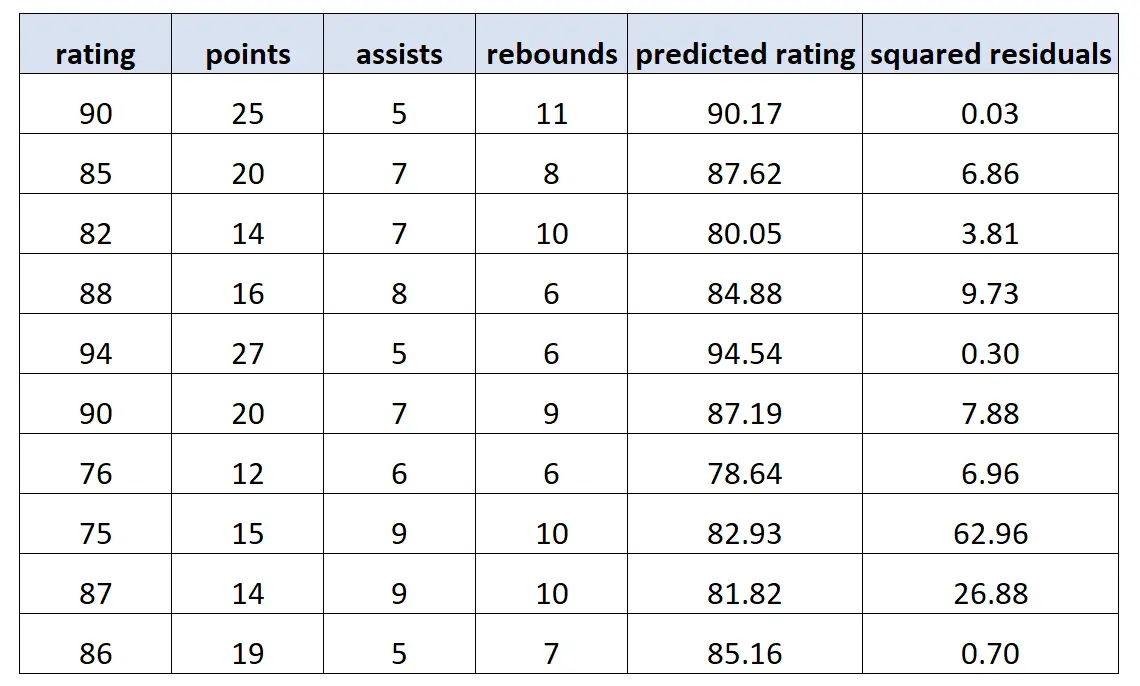
Następnie dopasowujemy nowy model regresji, wykorzystując kwadraty reszt jako wartości odpowiedzi i ponownie pierwotne zmienne predykcyjne jako zmienne predykcyjne. Znajdujemy następujące informacje:

• n: 10
• ^R2 _nowy : 0,600395

Zatem nasza statystyka testu Chi-kwadrat dla testu Breuscha-Pagana wynosi n*R ² _nowy = 10*.600395 = 6,00395 . Stopnie swobody to p = 3 zmienne predykcyjne.

Według kalkulatora wartości chi-kwadrat P , wartość p odpowiadająca ^X2 = 6,00395 z 3 stopniami swobody wynosi 0,111418 .

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej. Zakładamy zatem, że homoskedastyczność jest obecna.

Test Breuscha-Pagana w praktyce

Poniższe tutoriale zawierają przykłady krok po kroku wykonywania testu Breuscha-Pagana w różnych programach statystycznych:

Jak wykonać test Breuscha-Pagana w programie Excel
Jak wykonać test Breuscha-Pagana w R
Jak wykonać test Breuscha-Pagana w Pythonie
Jak wykonać test Breuscha-Pagana w Stata