Co to jest rozkład kategoryczny?
Rozkład kategoryczny to dyskretny rozkład prawdopodobieństwa, który opisuje prawdopodobieństwo, że zmienna losowa przyjmie wartość należącą do jednej z K kategorii, gdzie każda kategoria jest powiązana z prawdopodobieństwem.
Aby rozkład mógł zostać zaklasyfikowany jako rozkład kategoryczny, musi spełniać następujące kryteria:
- Kategorie są dyskretne.
- Istnieją dwie lub więcej potencjalnych kategorii.
- Prawdopodobieństwo, że zmienna losowa przyjmie wartość w każdej kategorii, musi mieścić się w przedziale od 0 do 1.
- Suma prawdopodobieństw wszystkich kategorii musi wynosić 1.
Najbardziej oczywistym przykładem rozkładu kategorycznego jest rozkład wyników związanych z rzutem kostką. Istnieje K = 6 potencjalnych wyników, a prawdopodobieństwo każdego wyniku wynosi 1/6:
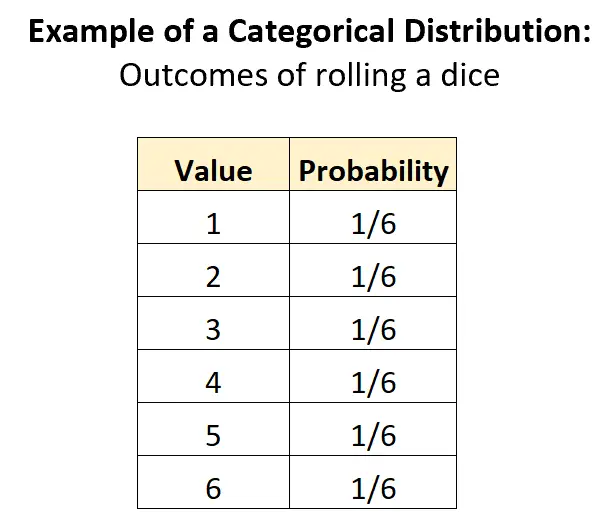
Rozkład ten spełnia wszystkie kryteria, aby można go było zaliczyć do rozkładu kategorycznego:
- Kategorie są dyskretne (np. zmienna losowa może przyjmować tylko wartości dyskretne – 1, 2, 3, 4, 5, 6)
- Istnieją dwie lub więcej potencjalnych kategorii.
- Prawdopodobieństwo każdej kategorii wynosi od 0 do 1.
- Suma prawdopodobieństw wynosi 1: 1/6 + 1/6 + 1/6 + 1/6 + 1/6 + 1/6 = 1.
Główna zasada:
Jeśli możesz policzyć liczbę wyników, to pracujesz z dyskretną zmienną losową – na przykład licząc, ile razy moneta wypadnie reszką.
Ale jeśli możesz zmierzyć wynik, pracujesz z ciągłą zmienną losową – na przykład mierząc wzrost, wagę, czas itp.
Inne przykłady rozkładów kategorycznych
W świecie rzeczywistym istnieje wiele rozkładów kategorycznych, w tym:
Przykład 1: Rzuć monetą.
Kiedy rzucamy monetą, istnieją 2 potencjalne, dyskretne wyniki, prawdopodobieństwo każdego wyniku wynosi od 0 do 1, a suma prawdopodobieństw jest równa 1:
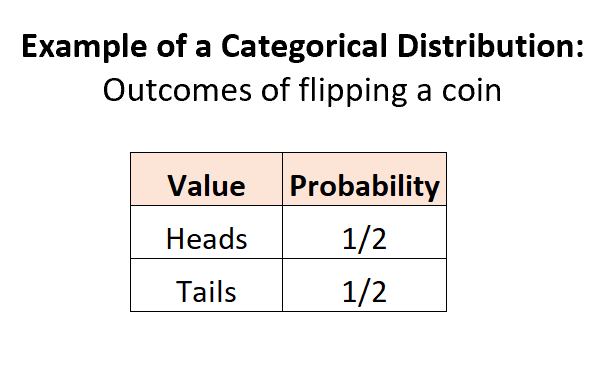
Przykład 2: Wybór kulek w urnie.
Załóżmy, że w urnie znajduje się 5 czerwonych kulek, 3 zielone kulki i 2 fioletowe kulki. Jeśli losowo wybierzemy kulę z urny, istnieją 3 potencjalne dyskretne wyniki, prawdopodobieństwo każdego wyniku wynosi od 0 do 1, a suma prawdopodobieństw wynosi 1:
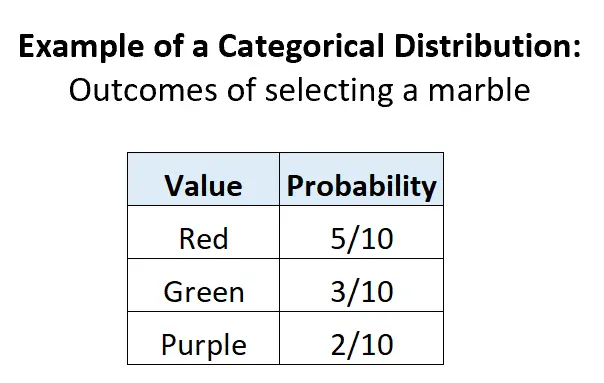
Przykład 3: Wybieranie karty z talii.
Jeśli losowo wybierzemy kartę ze standardowej talii 52 kart, istnieje 13 potencjalnych odrębnych wyników, prawdopodobieństwo każdego wyniku wynosi od 0 do 1, a suma prawdopodobieństw wynosi 1:
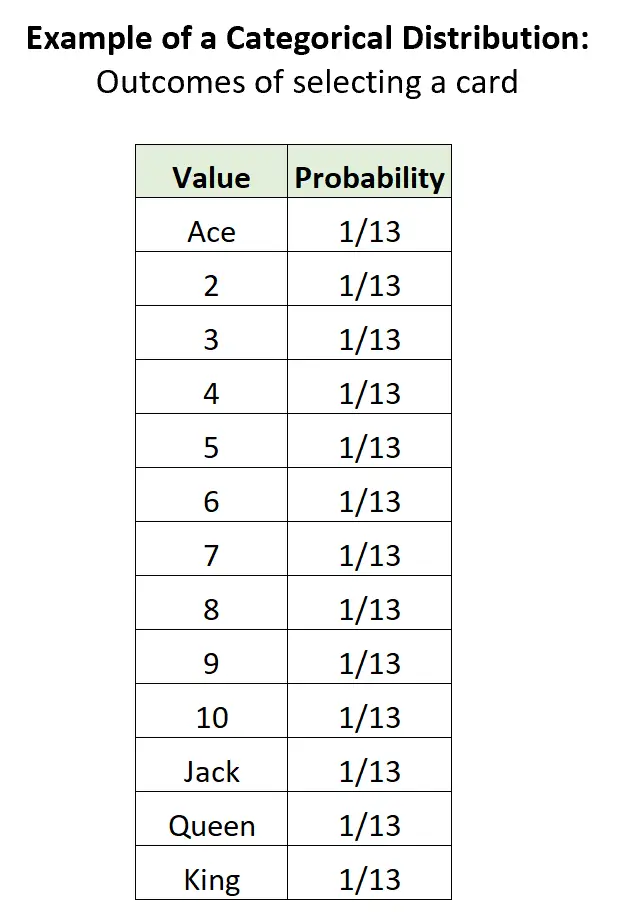
Związek z innymi dystrybucjami
Aby rozkład można było sklasyfikować jako rozkład kategoryczny , musi mieć K ≥ 2 potencjalnych wyników i n = 1 próbę.
Używając tej terminologii, rozkład kategoryczny jest podobny do następujących rozkładów:
Rozkład Bernoulliego: K = 2 wyniki, n = 1 test
Rozkład dwumianowy: K = 2 punkty końcowe, n ≥ 1 próba
Rozkład wielomianowy: K ≥ 2 wyniki, n ≥ próba
Dodatkowe zasoby
Co to są zmienne losowe?
Wprowadzenie do rozkładu dwumianowego
Wprowadzenie do rozkładu wielomianowego