Co to jest sturges? linijka? (definicja – przykład)
Histogram to wykres, który pomaga nam zwizualizować rozkład wartości w zestawie danych.
Okazuje się, że liczba pól użytych w histogramie może mieć ogromny wpływ na sposób interpretacji danych.
Jeśli użyjemy zbyt małej liczby grup, prawdziwy wzorzec leżący u podstaw danych może zostać ukryty:
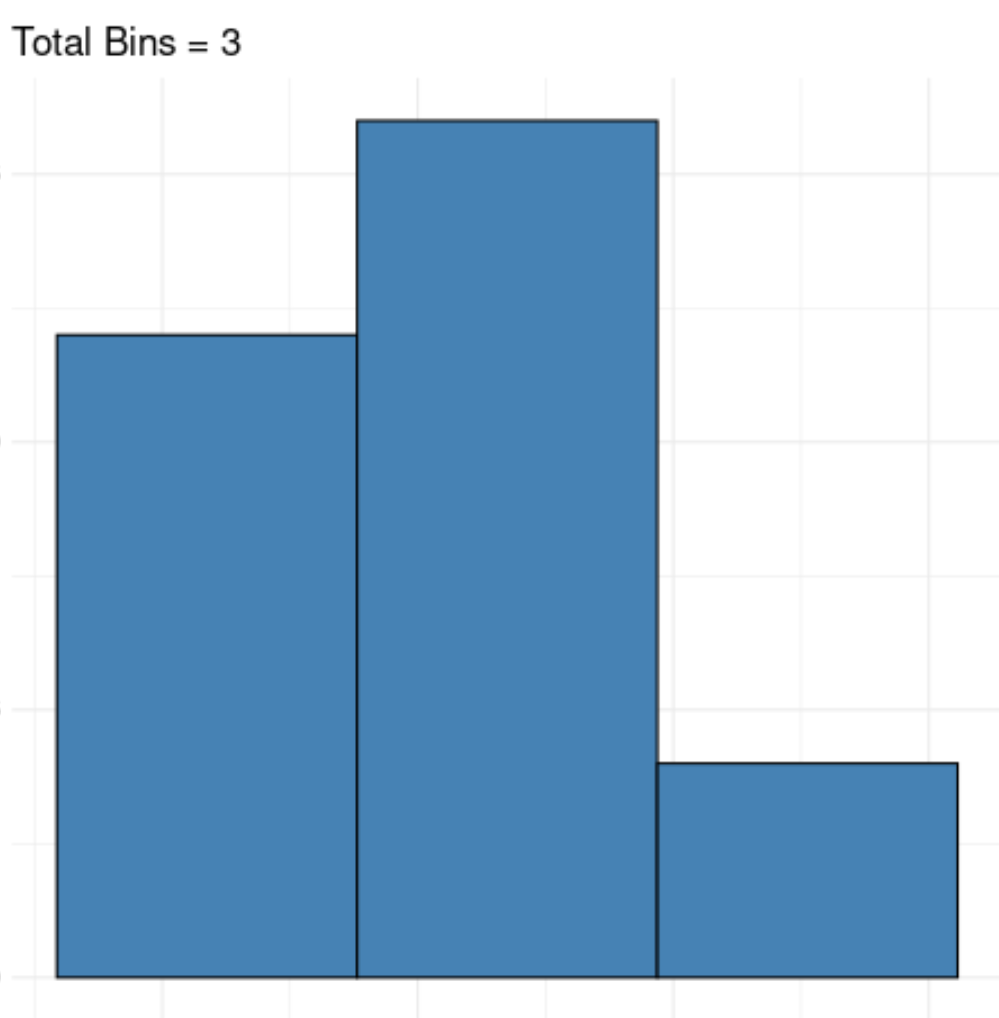
A jeśli użyjemy zbyt wielu grup, możemy po prostu zwizualizować szum w zbiorze danych:
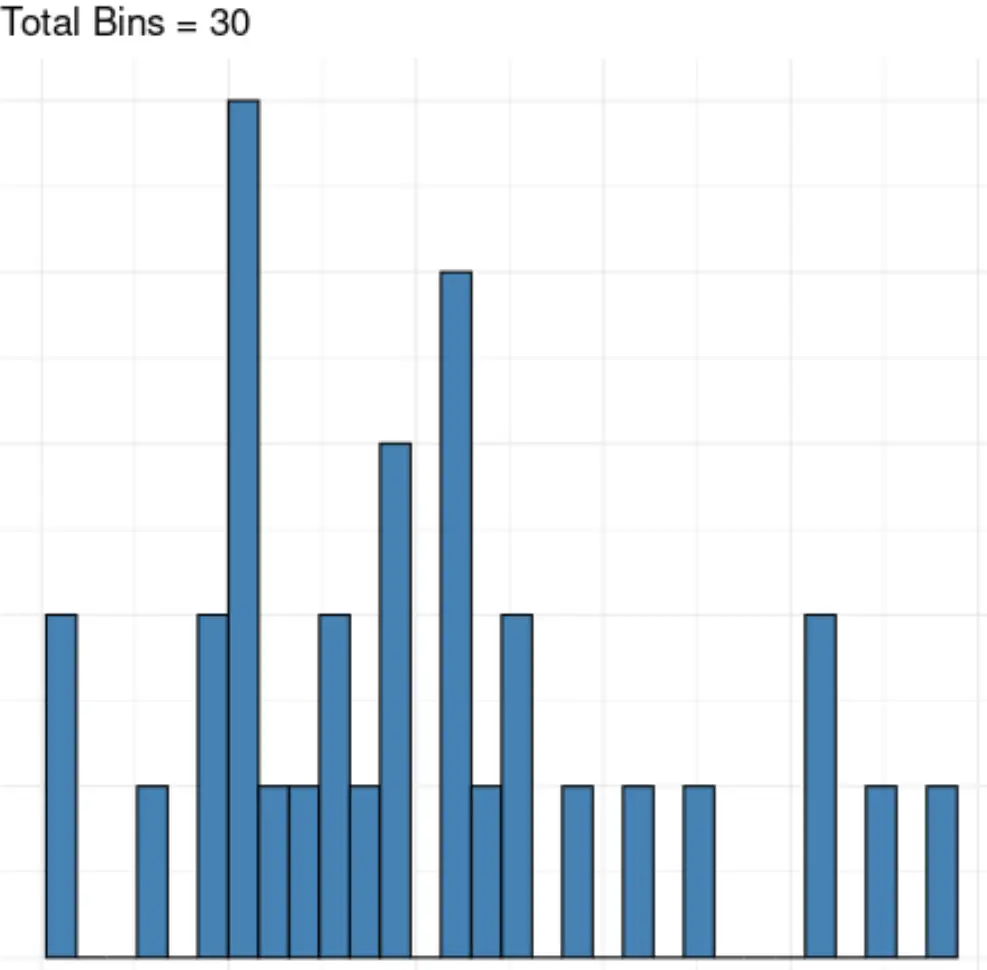
Na szczęście możemy zastosować metodę znaną jako reguła Sturgesa, aby określić optymalną liczbę pudełek do wykorzystania w histogramie.
Reguła Sturgesa wykorzystuje następujący wzór do określenia optymalnej liczby grup do wykorzystania w histogramie:
Optymalne pojemniki = ⌈log 2 n + 1⌉
Złoto:
- n: całkowita liczba obserwacji w zbiorze danych.
- ⌈ ⌉: Symbole oznaczające „sufit”, czyli zaokrąglanie odpowiedzi do najbliższej liczby całkowitej.
Przykład: reguła Sturgesa
Załóżmy, że mamy następujący zbiór danych zawierający łącznie n = 31 obserwacji:

Możemy skorzystać z reguły Sturgesa, aby określić optymalną liczbę pudełek, których należy użyć do wizualizacji tych wartości na histogramie:
Przedziały optymalne = ⌈log 2 (31) + 1⌉ = ⌈4,954 + 1⌉ = ⌈5,954⌉ = 6 .
Zgodnie z regułą Sturgesa w histogramie, którego używamy do wizualizacji tego rozkładu wartości, powinniśmy zastosować 6 przedziałów.
Tak wyglądałby histogram z 6 grupami dla tego zbioru danych:
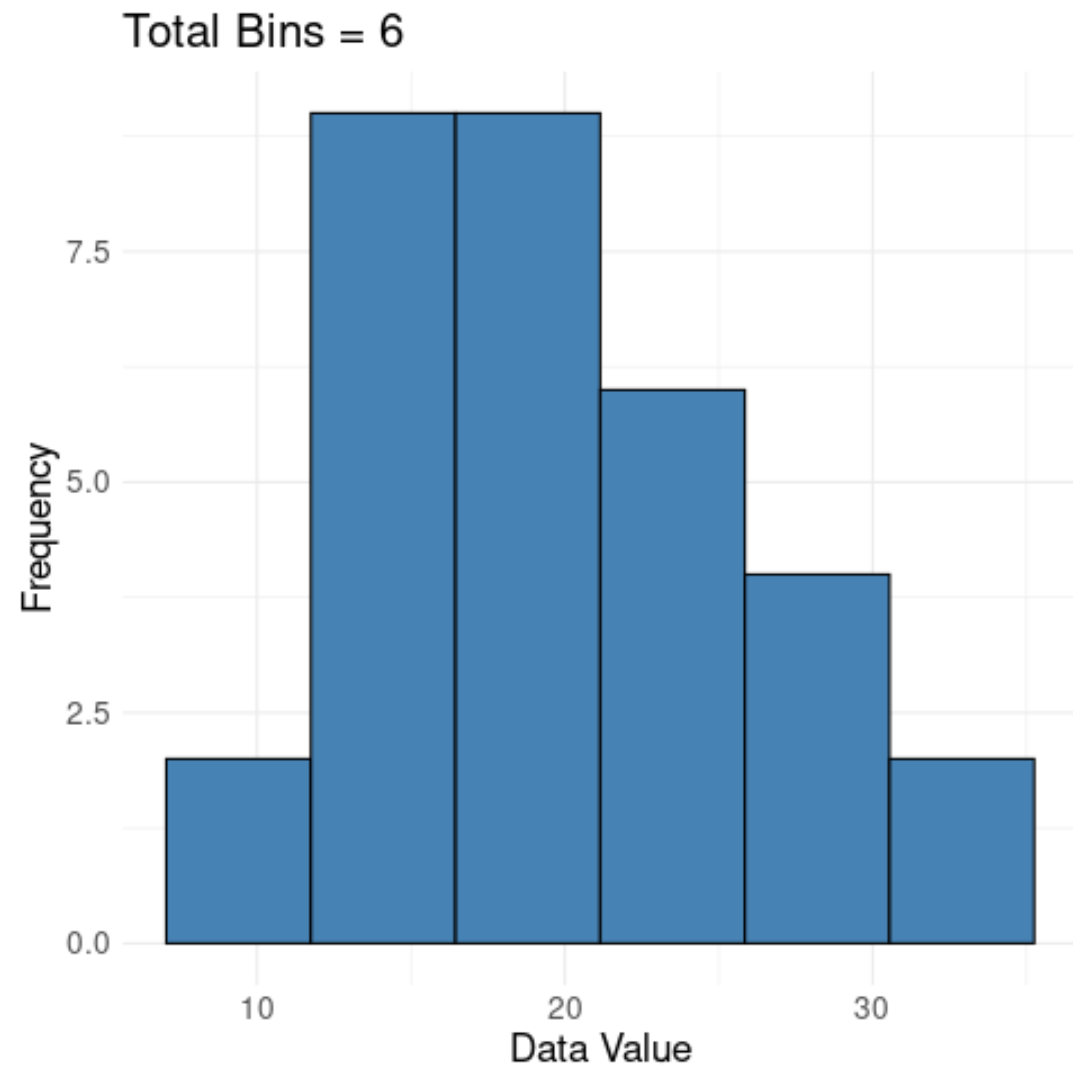
Zwróć uwagę, że wydaje się to wystarczające, aby dobrze zorientować się w podstawowym rozkładzie wartości, nie będąc zbyt licznymi, aby po prostu zwizualizować szum w danych.
Wspólne wartości reguły Sturgesa
Poniższa tabela przedstawia optymalną liczbę grup do wykorzystania w histogramie na podstawie całkowitej liczby obserwacji w zbiorze danych, zgodnie z regułą Sturgesa:
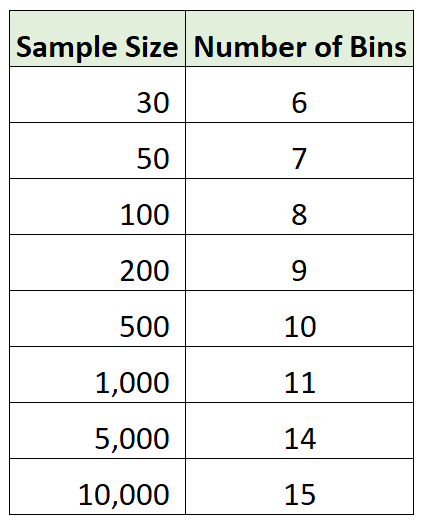
Alternatywy dla reguły Sturgesa
Reguła Sturgesa jest najczęstszą metodą określania optymalnej liczby pojemników do użycia w histogramie, ale istnieje kilka alternatywnych metod, w tym:
Zasada pierwiastka kwadratowego : Liczba pudełek = ⌈√ n ⌉
Zasada ryżu: Liczba pojemników = ⌈2 * 3 √ n ⌉
Reguła Freedmana-Diaconisa: Liczba pudełek = (2*IQR) / 3 √ n gdzie IQR jest rozstępem międzykwartylowym.
Bonus: Kalkulator reguł Sturgesa
Użyj tego bezpłatnego kalkulatora online, aby automatycznie zastosować regułę Sturgesa w celu określenia optymalnej liczby grup do użycia w histogramie na podstawie rozmiaru zbioru danych.