Co to jest test żywności? (wyjaśnienie i przykład)
Test Chow to test statystyczny opracowany przez ekonomistę Gregory’ego Chowa , który służy do sprawdzania, czy współczynniki dwóch różnych modeli regresji na różnych zbiorach danych są równe.
Test Chow jest zwykle stosowany w ekonometrii z danymi szeregów czasowych w celu ustalenia, czy w danym momencie występuje strukturalna przerwa w danych.
Rozważmy na przykład następujący wykres punktowy:
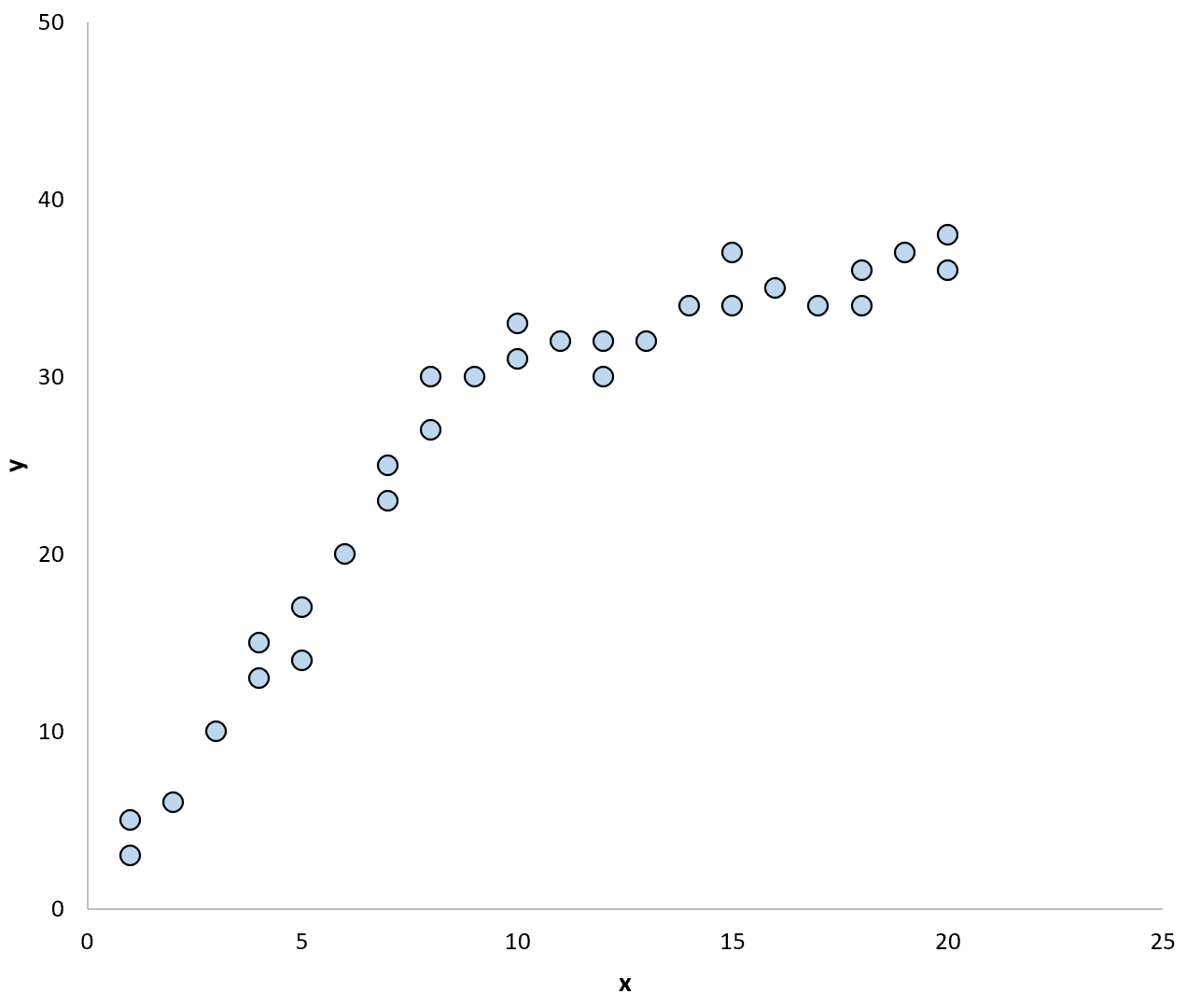
Gdybyśmy użyli linii regresji do podsumowania modelu w danych, mogłoby to wyglądać tak:
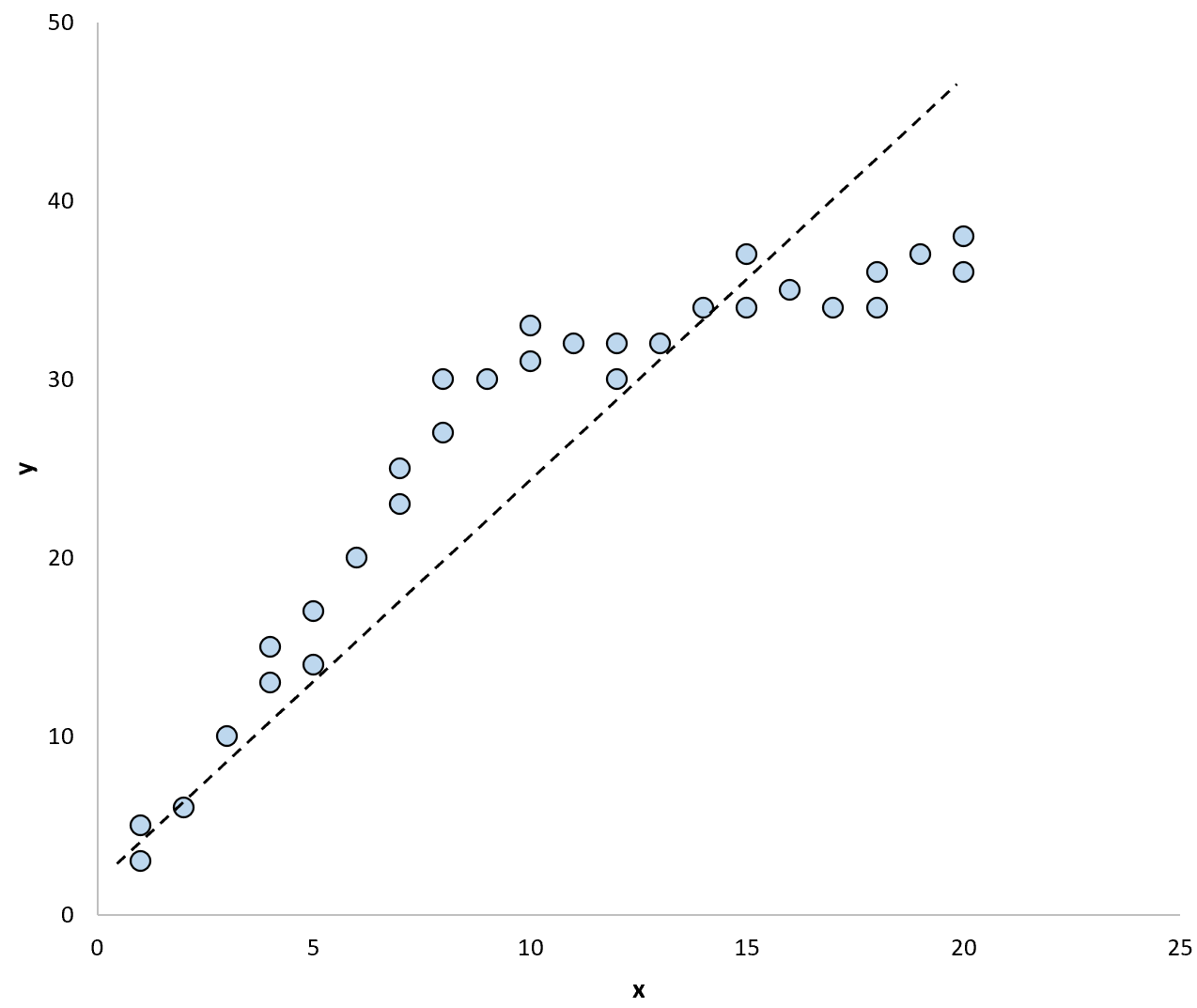
A gdybyśmy użyli dwóch oddzielnych linii regresji do podsumowania modelu w danych, mogłoby to wyglądać tak:
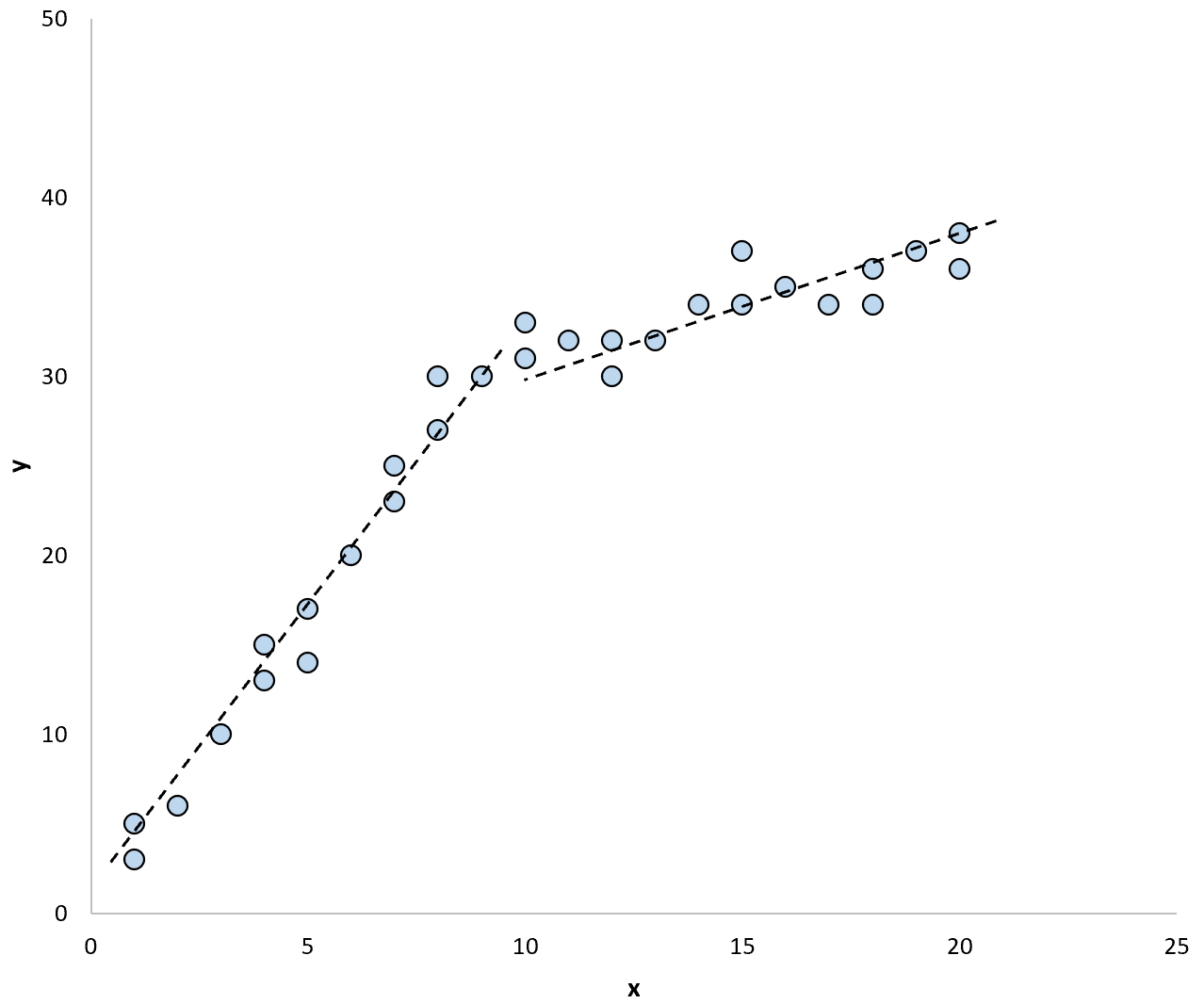
Test Chowa pozwala sprawdzić, czy współczynniki regresji każdej linii regresji są równe, czy nie.
Jeżeli test wykaże, że współczynniki nie są równe między liniami regresji, oznacza to, że istnieją istotne dowody na strukturalne uszkodzenie danych. Innymi słowy, trend danych jest bardzo różny przed i po tym strukturalnym punkcie załamania.
Kiedy stosować test Chow
Poniższe przykłady ilustrują sytuacje, w których warto wykonać test Chow:
1. Ustal, czy ceny akcji zmieniają się w różnym tempie przed wyborami i po nich.
2. Ustal, czy ceny domów zmieniają się przed i po zmianie stóp procentowych.
3. Ustalić, czy średni zysk przedsiębiorstw publicznych różni się przed i po przyjęciu nowego prawa podatkowego.
W każdej sytuacji możemy zastosować test Chow, aby określić, czy w danym momencie występuje strukturalny punkt załamania.
Kroki, aby wykonać test Chow
Aby wykonać test Chow, możemy wykonać następujące kroki.
Krok 1: Zdefiniuj hipotezę zerową i alternatywną.
Załóżmy, że dopasowujemy następujący model regresji do całego naszego zbioru danych:
- y t = a + bx 1t + cx t2 + ε
Następnie załóżmy, że dzielimy nasze dane na dwie grupy w oparciu o strukturalny punkt przerwania i dopasowujemy do każdej grupy następujące modele regresji:
- y t = za 1 + b 1 x 1 t + do 1 x t2 + ε
- y t = za 2 + b 2 x 1 t + do 2 x t2 + ε
Do testu Chowa użylibyśmy następujących hipotez zerowych i alternatywnych:
- Null (H 0 ): za 1 = za 2 , b 1 = b 2 i do 1 = do 2
- Alternatywa ( HA ): Przynajmniej jedno z porównań w Null nie jest równe.
Jeśli odrzucimy hipotezę zerową, będziemy mieli wystarczające dowody, aby stwierdzić, że w danych istnieje strukturalny punkt załamania i że dwie linie regresji mogą lepiej dopasować dane niż jedna.
Jeśli nie odrzucimy hipotezy zerowej, nie mamy wystarczających dowodów, aby stwierdzić, że w danych istnieje strukturalny punkt załamania. W tym przypadku mówimy, że linie regresji można „zgrupować” w jedną linię regresji, która wystarczająco dobrze reprezentuje wzór danych.
Krok 2: Oblicz statystykę testową.
Jeśli zdefiniujemy następujące pojęcia:
- ST : Suma kwadratów reszt wszystkich danych
- S 1 , S 2 : suma kwadratów reszt każdej grupy
- N 1 , N 2 : Liczba obserwacji w każdej grupie
- k: Liczba parametrów
Możemy wtedy powiedzieć, że statystyka testu Chow wynosi:
Statystyka testu Chowa = [(S T – (S 1 + S 2 ))/k] / [(S 1 + S 2 )/ (N 1 + N 2 -2k)]
Ta statystyka testowa jest zgodna z rozkładem F z k i N 1 + N 2 -2 k stopni swobody.
Krok 3: Odrzuć lub nie odrzucaj hipotezy zerowej.
Jeśli wartość p powiązana z tą statystyką testową jest poniżej pewnego poziomu istotności , możemy odrzucić hipotezę zerową i stwierdzić, że w danych występuje strukturalny punkt załamania.
Na szczęście większość programów statystycznych umożliwia wykonanie testu Chow, więc prawdopodobnie nigdy nie będziesz musiał przeprowadzać testu ręcznie.
Przykład wykonania testu Chow
Zapoznaj się z tym samouczkiem , aby zapoznać się z przykładem krok po kroku wykonania testu Chow dla danego zbioru danych w języku R.
Notatki z testu Chow
Oto kilka uwag, o których należy pamiętać na temat testu Chow:
1. W teście założono, że reszty modeli regresji mają rozkład niezależny i identyczny z rozkładu normalnego o nieznanej wariancji.
2. Test Chow powinien być stosowany tylko wtedy, gdy pęknięcie konstrukcyjne, które chcesz sprawdzić, następuje w znanym czasie. Innymi słowy, nie należy wielokrotnie stosować testu w celu ustalenia, czy dany moment można uznać za pęknięcie konstrukcyjne.