Co to jest test q cochrana? (definicja – przykład)

Test Q Cochrana to test statystyczny stosowany do określenia, czy proporcja „sukcesów” jest równa w trzech lub większej liczbie grup, w których w każdej grupie występują te same osoby.

Na przykład możemy użyć testu Q Cochrana, aby określić, czy odsetek uczniów, którzy zdali test, jest równy przy zastosowaniu trzech różnych technik uczenia się.

Etapy wykonywania testu Q Cochrana

Test Q Cochrana wykorzystuje następujące hipotezy zerowe i alternatywne:

Hipoteza zerowa (H ₀ ): Proporcja „sukcesów” jest taka sama we wszystkich grupach

Hipoteza alternatywna ( _HA ): Proporcja „sukcesów” jest różna w co najmniej jednej z grup

Statystykę testową oblicza się w następujący sposób:

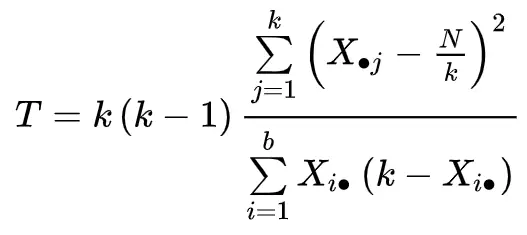
Złoto:

• k: Liczba zabiegów (lub „grup”)
• Xj: suma kolumny dla ^j- tego zabiegu
• b: Liczba bloków
• Xi. : Suma linii dla ^i-tego bloku
• N: Całkowita suma

Statystyka testu T jest zgodna z rozkładem Chi-kwadrat z k-1 stopniami swobody.

Jeśli wartość p powiązana ze statystyką testową jest poniżej pewnego poziomu istotności (takiego jak α = 0,05), możemy odrzucić hipotezę zerową i stwierdzić, że mamy wystarczające dowody, aby stwierdzić, że proporcja „sukcesów” jest inna w przynajmniej jednej z grup.

Przykład: test Q Cochrana

Załóżmy, że badacz chce wiedzieć, czy trzy różne techniki uczenia się prowadzą do różnych proporcji wskaźników sukcesu wśród uczniów.

Aby to sprawdzić, rekrutuje 20 uczniów, z których każdy zdaje egzamin o równym stopniu trudności, stosując trzy różne techniki nauki. Wyniki przedstawiono poniżej:

Do wykonania testu Q Cochrana możemy użyć oprogramowania statystycznego, ponieważ wykonywanie go ręcznie może być żmudne.

Oto kod, którego możemy użyć do utworzenia tego zbioru danych i wykonania testu Q Cochrana w statystycznym języku programowania R:

 #load DescTools package
library (DescTools)

#create dataset
df <- data.frame(student= rep (1:20, each = 3 ),
                 technique= rep (c('A', 'B', 'C'), times= 20 ),
                 outcome=c(1, 1, 0, 1, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 1,
                           1, 1, 0, 1, 0, 1, 0, 0, 0, 0, 1, 0, 0, 1, 1,
                           1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1,
                           1, 0, 0, 0, 1, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1))

#perform Cochran's Q test
CochranQTest(outcome ~ technique| student, data=df)

	Cochran's Q test

data: outcome and technique and student
Q = 0.33333, df = 2, p-value = 0.8465

Na podstawie wyniku testu możemy zaobserwować, co następuje:

• Statystyka testowa wynosi 0,333
• Odpowiednia wartość p wynosi 0,8465

Ponieważ ta wartość p jest nie mniejsza niż 0,05, nie możemy odrzucić hipotezy zerowej.

Oznacza to, że nie mamy wystarczających dowodów, aby stwierdzić, że technika uczenia się stosowana przez uczniów prowadzi do różnych proporcji wskaźników sukcesu.