Wprowadzenie do rozkładu trójkątnego
Rozkład trójkątny jest ciągłym rozkładem prawdopodobieństwa z funkcją gęstości prawdopodobieństwa w kształcie trójkąta.
Jest ona definiowana przez trzy wartości:
- Wartość minimalna ma
- Maksymalna wartość B
- Maksymalna wartość c
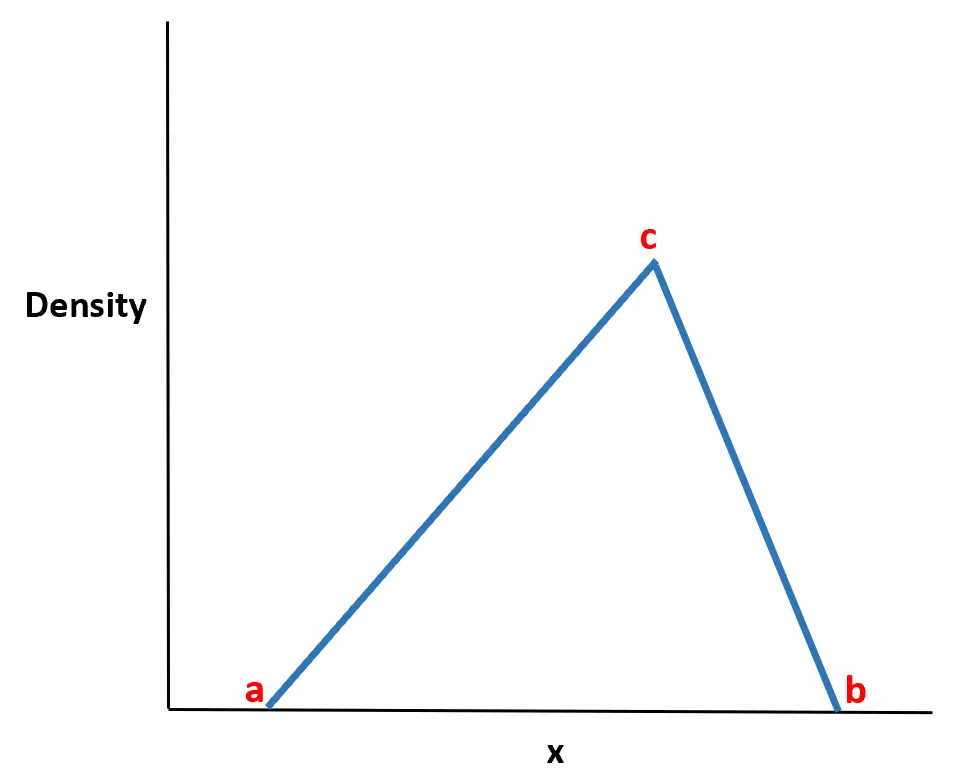
Nazwa rozkładu wzięła się stąd, że funkcja gęstości prawdopodobieństwa ma kształt trójkąta.
Okazuje się, że rozkład ten jest niezwykle przydatny w świecie rzeczywistym, ponieważ często możemy oszacować wartość minimalną (a), wartość maksymalną (b) i najbardziej prawdopodobną wartość (c), jaką przyjmie zmienna losowa . często może modelować zachowanie zmiennych losowych przy użyciu rozkładu trójkątnego, znając tylko te trzy wartości.
Na przykład restauracja może oszacować, że jej łączna sprzedaż w nadchodzącym tygodniu wyniesie co najmniej 10 000 USD, maksymalnie 30 000 USD i najprawdopodobniej 25 000 USD.

Używając tylko tych trzech liczb, mogliby zastosować rozkład trójkątny do określenia prawdopodobieństwa dokonania określonej liczby sprzedaży.
Własności rozkładu trójkątnego
Rozkład trójkątny ma następujące właściwości:
PDF:
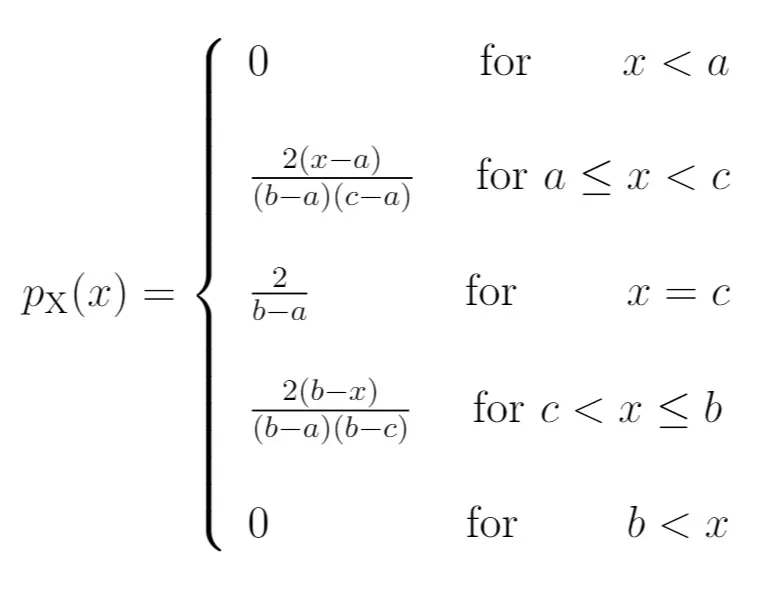
CDF:
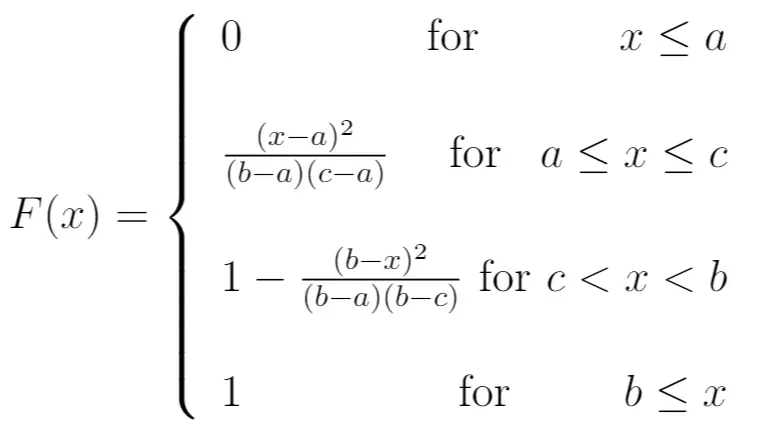
Średnia: (a + b + c) / 3
Tryb: ok
Wariancja: (a 2 + b 2 + c 2 – ab – ac – bc) / 18
Przykład wykorzystania rozkładu trójkątnego
Wróćmy do poprzedniego przykładu. Załóżmy, że restauracja szacuje, że jej łączna sprzedaż w nadchodzącym tygodniu wyniesie co najmniej 10 000 USD, maksymalnie 30 000 USD i najprawdopodobniej 25 000 USD.

Jakie jest prawdopodobieństwo, że łączna sprzedaż restauracji będzie mniejsza niż 20 000 USD?
Aby odpowiedzieć na to pytanie, możemy zadać x = sprzedaż całkowita. Wiemy, że x leży pomiędzy minimalną wartością a wynoszącą 10 000 dolarów a maksymalną wartością c wynoszącą 25 000 dolarów.
Zatem zgodnie z plikiem PDF możemy użyć następującego równania, aby znaleźć prawdopodobieństwo, że łączna sprzedaż restauracji będzie mniejsza niż 20 000 USD:
- P(X < 20 000 USD) = (xa) 2 / ((ba) (ca))
- P(X < 20 000 USD) = (20 000–10 000) 2 / ((30 000–10 000) (25 000–10 000))
- P(X <20 000 USD) = 0,333
Prawdopodobieństwo, że łączna sprzedaż restauracji będzie mniejsza niż 20 000 USD, wynosi 0,333 .
Jaka jest średnia oczekiwana sprzedaż w restauracji?
Oczekiwaną średnią sprzedaż możemy obliczyć korzystając ze wzoru na wcześniej podaną średnią:
- Średnia = (a + b + c) / 3
- Średnia = (10 000 USD + 30 000 USD + 25 000 USD) / 3
- Średnia = 21 667 dolarów
Średnia oczekiwana sprzedaż wynosi 21 667 .
Dodatkowe zasoby
Poniższe samouczki zawierają wprowadzenie do innych powszechnie używanych dystrybucji:
Rozkład normalny
Rozkład dwumianowy
Dystrybucja ryb
Rozkład geometryczny