Jaka jest jaźń morana? (definicja – przykład)
I Morana to sposób pomiaru autokorelacji przestrzennej.
Mówiąc najprościej, jest to sposób na ilościowe określenie, jak blisko wartości są skupione w przestrzeni 2D. Jest często stosowany w geografii i informatyce geograficznej (GIS) do pomiaru stopnia zgrupowania różnych obiektów na mapie, takich jak dochód gospodarstwa domowego, poziom wykształcenia itp.
Moran I: formuła
Wzór na obliczenie I Morana to:
I = (N/W)*ΣΣw ij (x i – x )(x j – x )/Σ(x i – x ) 2
Złoto:
- N: Liczba jednostek przestrzennych indeksowanych przez i oraz j
- W: Suma wszystkich w ij
- x: Zmienna odsetek (dochód gospodarstwa domowego, lata nauki itp.)
- x : Średnia z x
- w ij : Macierz wag przestrzennych
Prawdopodobnie nigdy nie będziesz musiał obliczać tego pomiaru ręcznie, ponieważ większość programów statystycznych może to obliczyć za Ciebie, ale warto znać wzór używany pod maską.
Wartość Morana I może wynosić od -1 do 1, gdzie:
- -1: Interesująca zmienna jest doskonale rozproszona
- 0: interesująca zmienna jest losowo rozproszona
- 1: Interesująca zmienna jest doskonale pogrupowana
Oprócz obliczania współczynnika Morana większość programów statystycznych oblicza odpowiednią wartość p, której można użyć do określenia, czy dane są losowo rozproszone, czy nie.
Test Morana wykorzystuje następujące hipotezy zerowe i alternatywne:
Hipoteza zerowa (H 0 ): dane są losowo rozproszone.
Hipoteza alternatywna ( HA ): Dane nie są losowo rozproszone, to znaczy są pogrupowane w widoczne wzorce.
Jeśli wartość p odpowiadająca I Morana jest poniżej pewnego poziomu istotności (tj. α = 0,05), wówczas możemy odrzucić hipotezę zerową i stwierdzić, że dane są grupowane przestrzennie przez w taki sposób, że jest mało prawdopodobne, aby były skupione przestrzennie. wydarzyło się przez przypadek.
Moran I: kilka przykładów
Poniższe przykłady przedstawiają fałszywe karty o różnych wartościach I Morana.
Załóżmy, że każdy kwadrat na mapie reprezentuje hrabstwo, a hrabstwa o średnich dochodach gospodarstwa domowego powyżej 50 000 dolarów są zaznaczone na niebiesko.
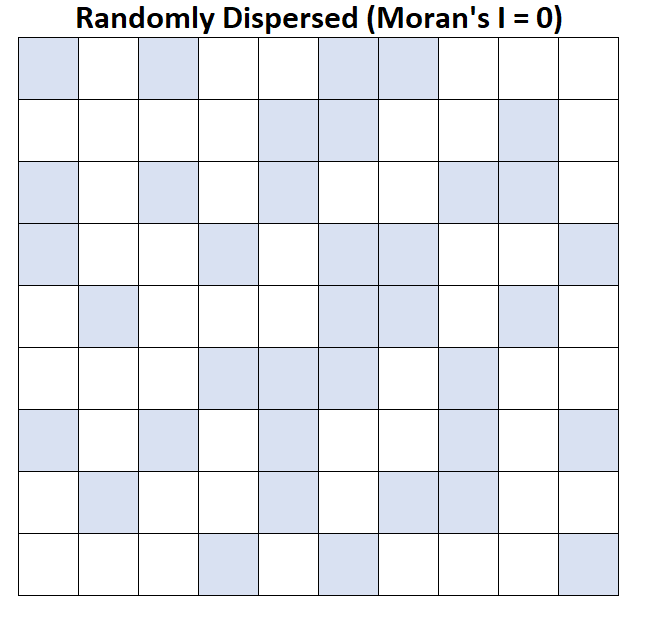
I Morana = 0: Średni dochód gospodarstwa domowego jest losowo rozproszony (tj. losowe skupienia w losowych obszarach).
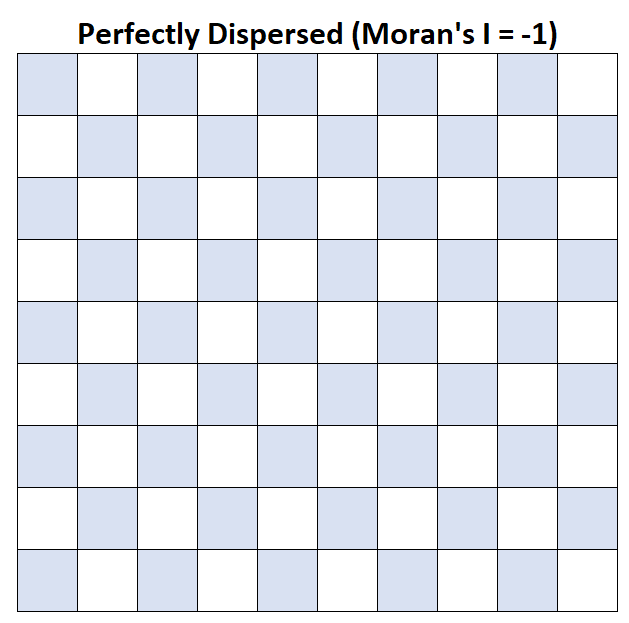
Moran’s I = -1: Przeciętny dochód gospodarstwa domowego jest doskonale rozproszony.
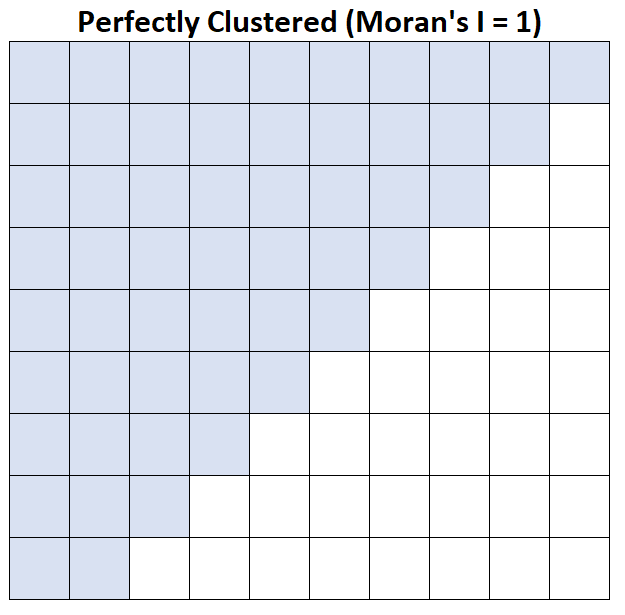
I Morana = 1: średni dochód gospodarstwa domowego jest doskonale pogrupowany.
W tym przykładzie znajdziesz konkretny przykład obliczenia I Morana w oprogramowaniu statystycznym R.