Rozkład symetryczny: definicja + przykłady

W statystyce rozkład symetryczny to taki, w którym lewa i prawa strona odzwierciedlają się nawzajem.

Najbardziej znanym rozkładem symetrycznym jest rozkład normalny , który ma wyraźny kształt dzwonu.

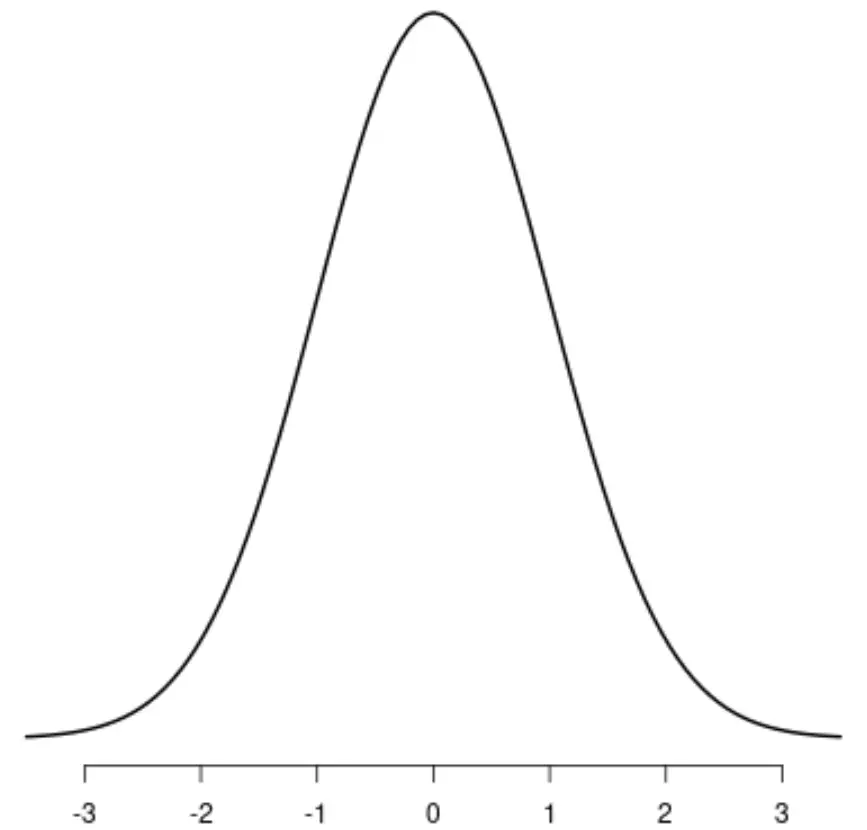
Jeśli narysowałbyś linię przez środek rozkładu, lewa i prawa strona rozkładu idealnie by się odzwierciedlały:

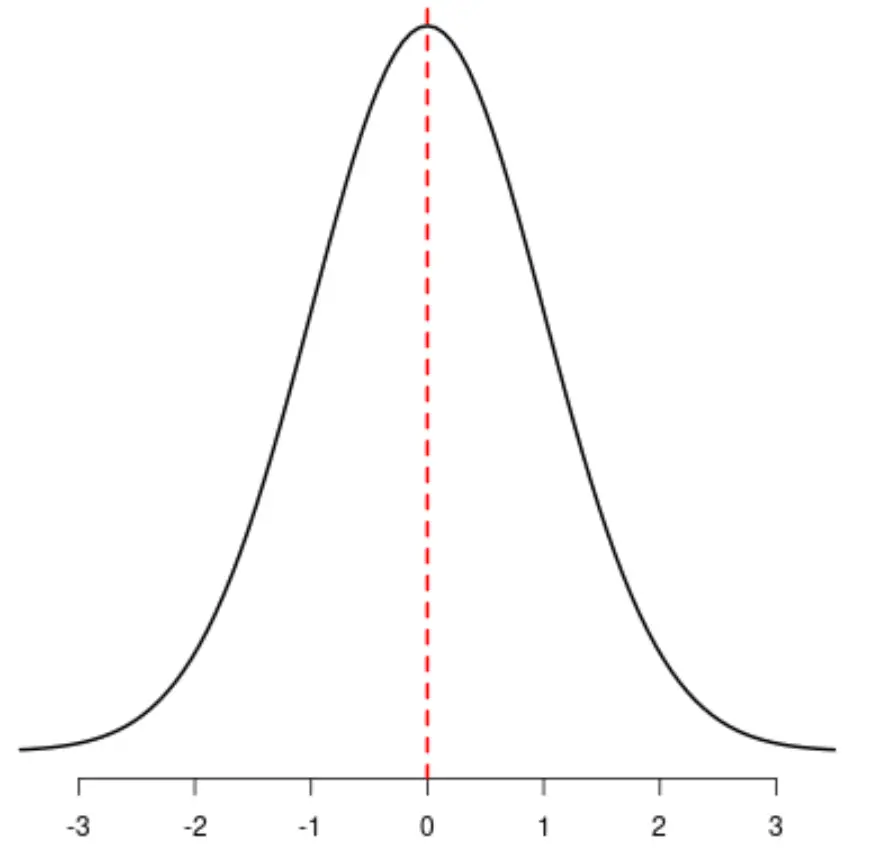
W statystyce skośność jest sposobem opisu symetrii rozkładu. Wartość ta może być ujemna, zerowa lub dodatnia.

W przypadku rozkładów symetrycznych asymetria wynosi zero.

Kontrastuje to z rozkładami lewostronnymi, które mają ujemną skośność:

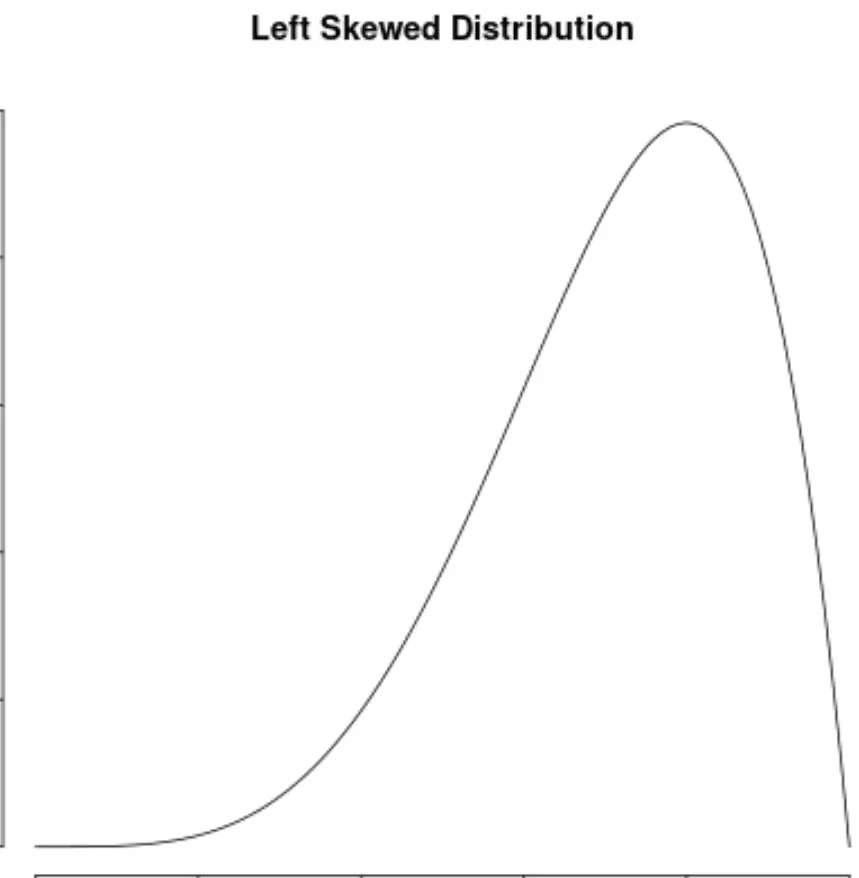
Kontrastuje to również z rozkładami prawoskrętnymi, które mają dodatnią skośność:

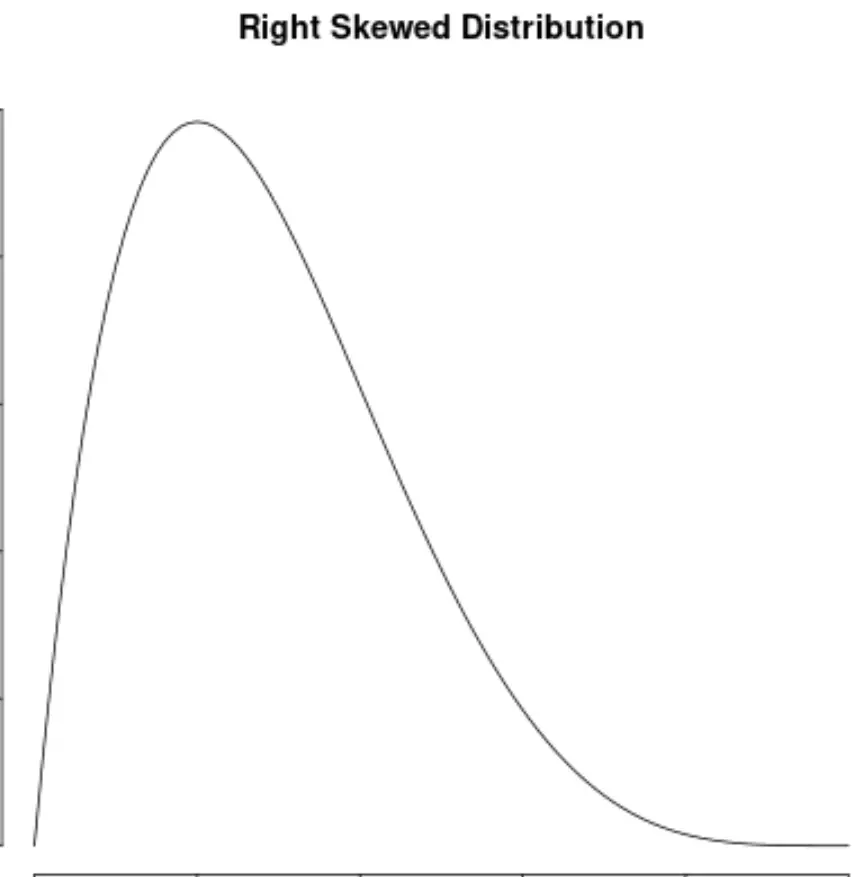
Własności rozkładów symetrycznych

W rozkładzie symetrycznym średnia, mediana i moda są równe.

Zapamiętaj następujące definicje każdego z nich:

• Średnia: średnia wartość.
• Mediana: wartość średnia.
• Tryb: wartość, która pojawia się najczęściej.

W rozkładzie symetrycznym każda z tych wartości jest sobie równa.

W każdym z dotychczasowych przykładów używaliśmy jako przykładu rozkładów jednomodalnych – rozkładów z tylko jednym „szczytem”. Jednakże rozkład może być również bimodalny i symetryczny.

Rozkład bimodalny to rozkład, który ma dwa piki.

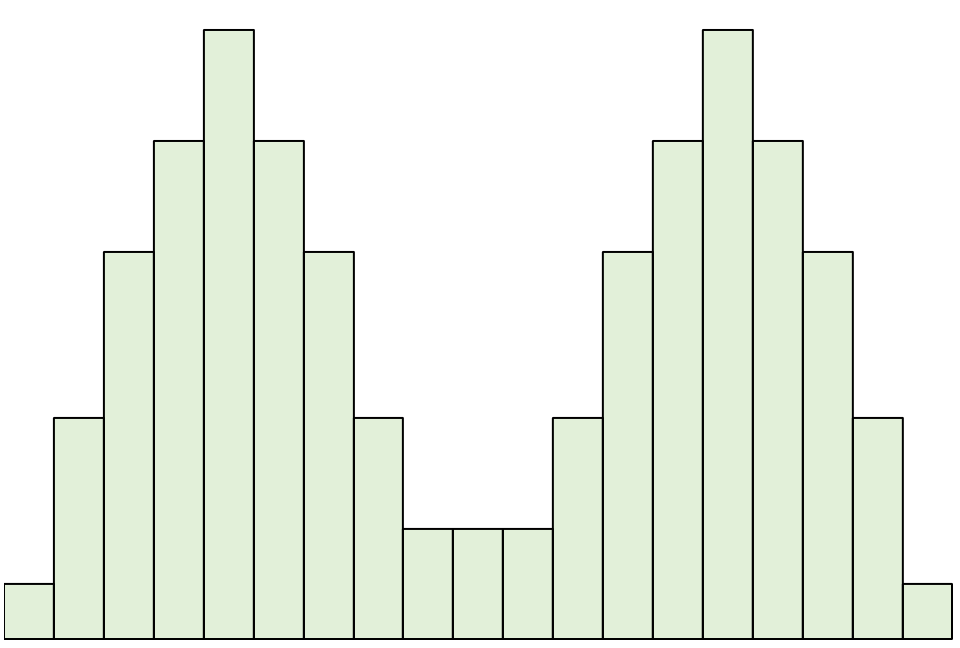
Zauważ, że jeśli narysujemy linię przez środek tego rozkładu, lewa i prawa strona nadal będą się odzwierciedlać.

W przypadku tych rozkładów średnia i mediana są równe. Jednakże mod leży w obu wierzchołkach.

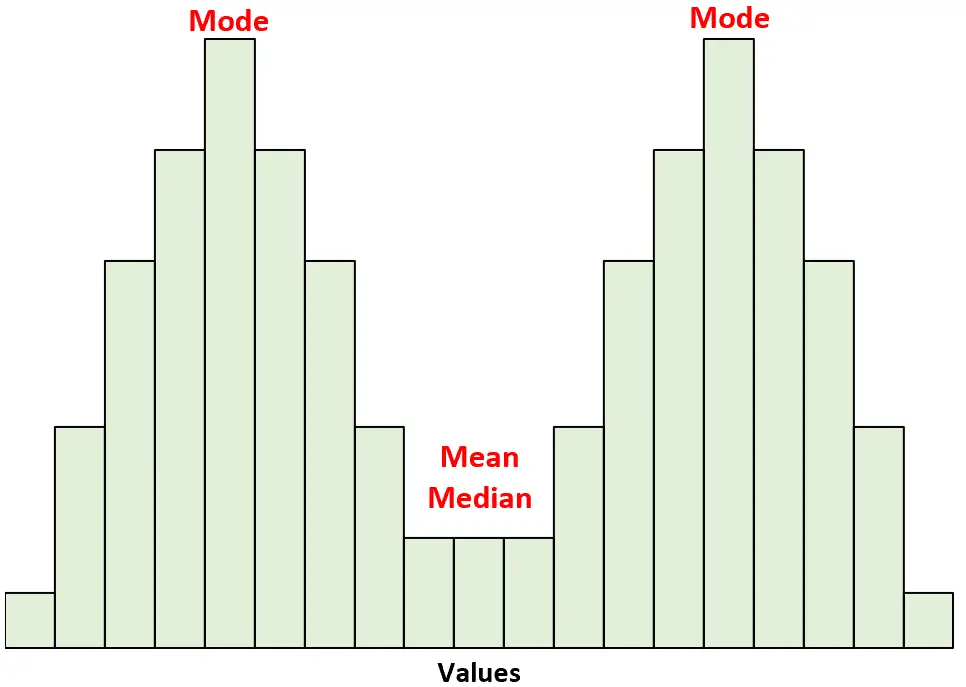
Inne przykłady rozkładów symetrycznych

Oprócz rozkładu normalnego symetryczne są także następujące rozkłady:

Dystrybucja t

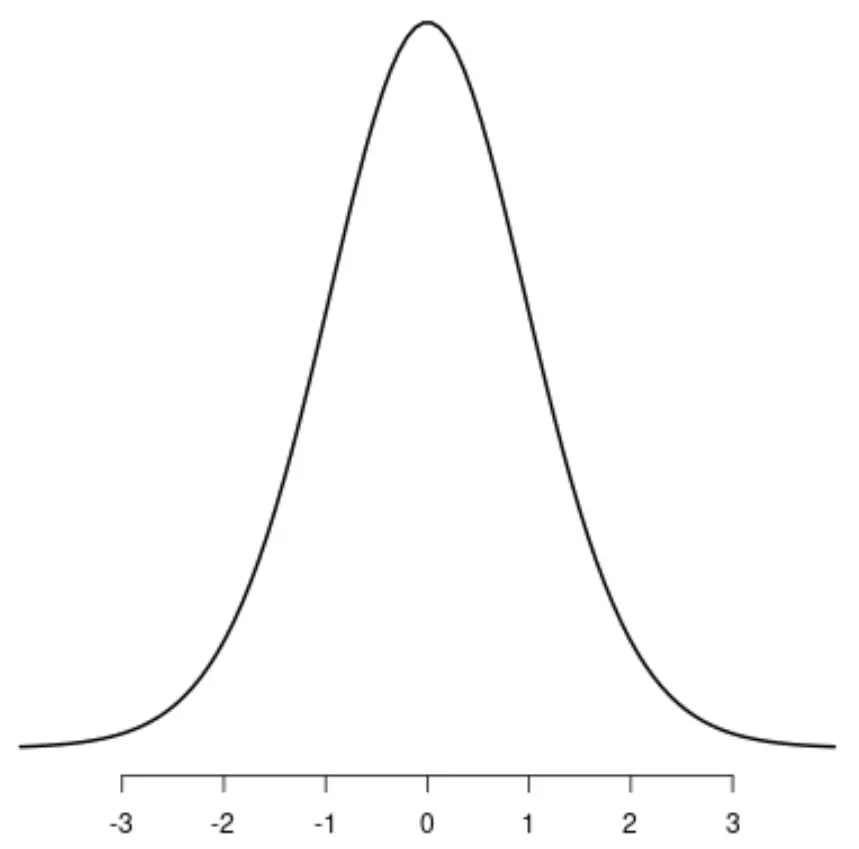
Równomierna dystrybucja

Rozkład Cauchy’ego

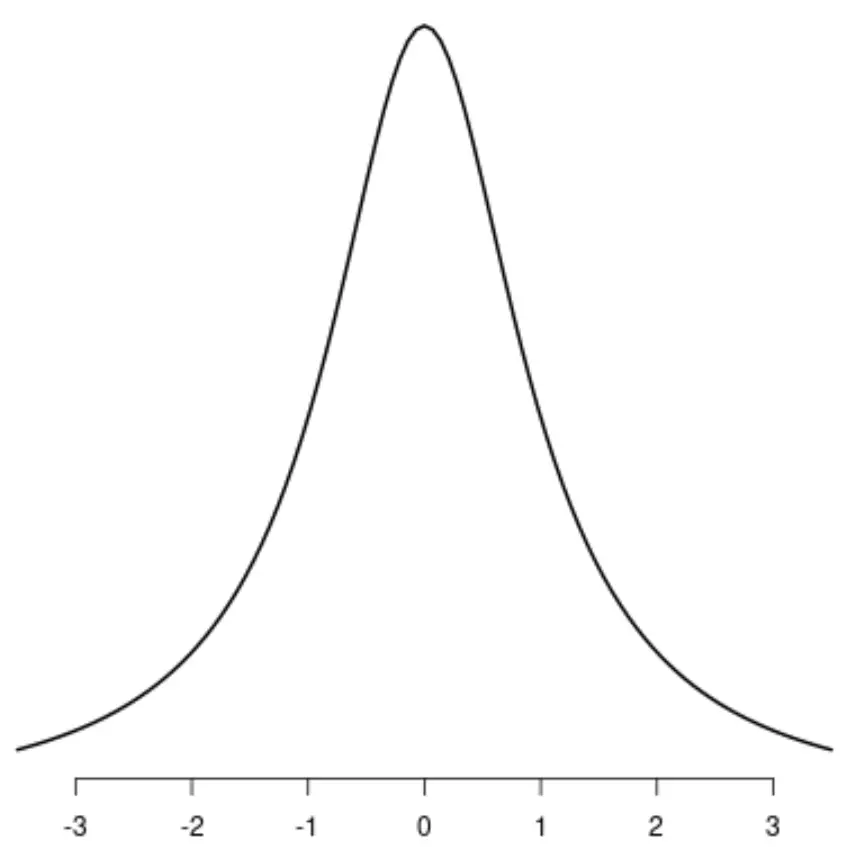
Jeśli narysujesz linię przez środek jednego z tych rozkładów, lewa i prawa strona każdego rozkładu będą doskonale odzwierciedlać siebie.

Rozkłady symetryczne i centralne twierdzenie graniczne

Jednym z najważniejszych twierdzeń we wszystkich statystykach jest centralne twierdzenie graniczne, które stwierdza, że rozkład próbkowania średniej próbki jest w przybliżeniu normalny, jeśli wielkość próby jest wystarczająco duża, nawet jeśli rozkład populacji nie jest normalny .

Aby zastosować centralne twierdzenie graniczne, wielkość próby musi być wystarczająco duża. Okazuje się, że dokładnie to, ile osób jest „wystarczająco dużych”, zależy od leżącego u podstaw kształtu rozkładu populacji.

Zwłaszcza:

• Jeśli rozkład populacji jest symetryczny, czasami wystarczająca jest wielkość próby wynosząca zaledwie 15 osób.
• Jeśli rozkład populacji jest nierówny, zwykle konieczna jest próba licząca co najmniej 30 osób.
• Jeżeli rozkład populacji jest wyjątkowo nierówny, konieczna może być próba licząca 40 lub więcej osób.

Zatem zaletą rozkładów symetrycznych jest to, że potrzebujemy mniejszych próbek, aby zastosować centralne twierdzenie graniczne podczas obliczania przedziałów ufności lub testowania hipotez .

Dodatkowe zasoby

Wprowadzenie do centralnego twierdzenia granicznego
Co to jest rozkład bimodalny?
Przewodnik po rozkładach skośnych w lewo i w prawo