Jak znaleźć średnią rozkładu prawdopodobieństwa: z przykładami

Rozkład prawdopodobieństwa mówi nam, jakie jest prawdopodobieństwo, że zmienna losowa przyjmie określone wartości.

Na przykład poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że dana drużyna piłkarska zdobędzie określoną liczbę bramek w danym meczu:

Uwaga: prawdopodobieństwa w prawidłowym rozkładzie prawdopodobieństwa zawsze będą sumować się do 1. Możemy potwierdzić, że ten rozkład prawdopodobieństwa jest prawidłowy: 0,18 + 0,34 + 0,35 + 0,11 + 0,02 = 1.

Aby znaleźć średnią (czasami nazywaną „wartością oczekiwaną”) rozkładu prawdopodobieństwa, możemy skorzystać z następującego wzoru:

 Mean (Or "Expected Value") of a Probability Distribution:

μ = Σx * P(x)

where:
•x: Data value
    •P(x): Probability of value

Rozważmy na przykład nasz rozkład prawdopodobieństwa dla drużyny piłkarskiej:

Średnią liczbę bramek drużyny piłkarskiej oblicza się w następujący sposób:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 gola.

Poniższe przykłady pokazują, jak obliczyć średnią rozkładu prawdopodobieństwa w kilku innych scenariuszach.

Przykład 1: Średnia liczba awarii pojazdów

Poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że w danym pojeździe wystąpi określona liczba awarii akumulatora w okresie 10 lat:

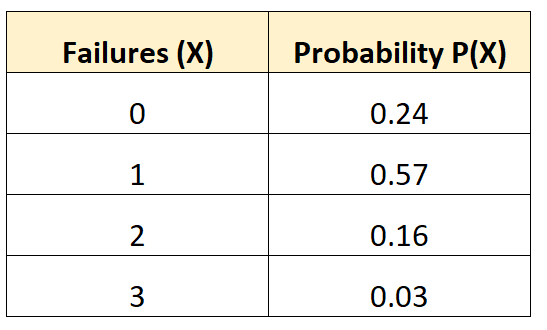
Pytanie: Jaka jest średnia liczba awarii przewidywanych dla tego pojazdu?

Rozwiązanie: Średnią liczbę oczekiwanych awarii oblicza się w następujący sposób:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 awarii.

Przykład 2: średnia liczba zwycięstw

Poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że dana drużyna koszykówki wygra określoną liczbę meczów w turnieju:

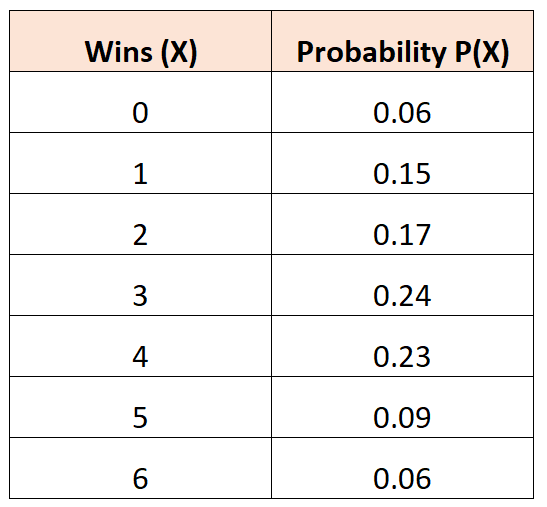
Pytanie: Jaka jest średnia liczba zwycięstw oczekiwanych przez tę drużynę?

Rozwiązanie: Średnią liczbę oczekiwanych zwycięstw oblicza się w następujący sposób:

μ = 0*0,06 + 1*0,15 + 2*0,17 + 3*0,24 + 4*0,23 + 5*0,09 + 6*0,06 = 2,94 zwycięstw.

Przykład 3: średnia liczba sprzedaży

Poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że dany sprzedawca dokona określonej liczby sprzedaży w nadchodzącym miesiącu:

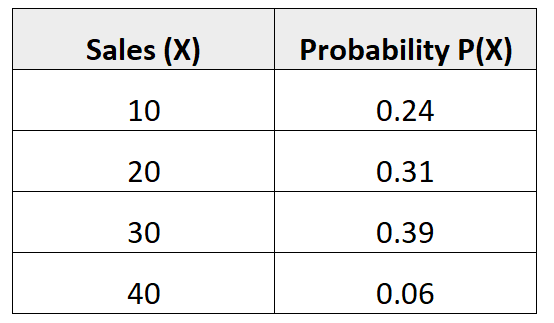
Pytanie: Jaka jest średnia liczba sprzedaży oczekiwana dla tego sprzedawcy w nadchodzącym miesiącu?

Rozwiązanie: Średnią liczbę oczekiwanej sprzedaży oblicza się w następujący sposób:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 brudny.

Bonus: Kalkulator rozkładu prawdopodobieństwa

Możesz użyć tego kalkulatora, aby automatycznie obliczyć średnią dowolnego rozkładu prawdopodobieństwa.