Jak znaleźć odchylenie standardowe rozkładu prawdopodobieństwa

Rozkład prawdopodobieństwa mówi nam, jakie jest prawdopodobieństwo, że zmienna losowa przyjmie określone wartości.

Na przykład poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że dana drużyna piłkarska zdobędzie określoną liczbę bramek w danym meczu:

Aby znaleźć odchylenie standardowe rozkładu prawdopodobieństwa, możemy skorzystać z następującego wzoru:

σ = √ Σ(x _i -μ) ² * P(x _i )

Złoto:

• x _i : ^i-ta wartość
• μ: średnia rozkładu
• P(x _i ): Prawdopodobieństwo ^i-tej wartości

Rozważmy na przykład nasz rozkład prawdopodobieństwa dla drużyny piłkarskiej:

Średnią liczbę bramek drużyny piłkarskiej oblicza się w następujący sposób:

μ = 0*0,18 + 1*0,34 + 2*0,35 + 3*0,11 + 4*0,02 = 1,45 gola.

Moglibyśmy wówczas obliczyć odchylenie standardowe w następujący sposób:

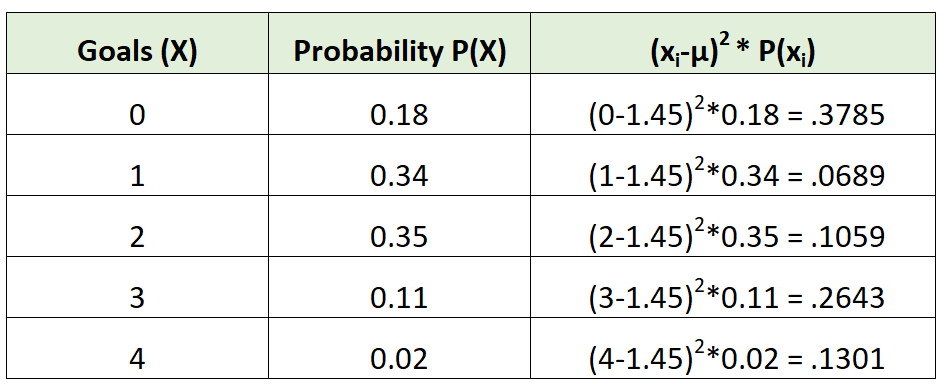
Odchylenie standardowe to pierwiastek kwadratowy z sumy wartości w trzeciej kolumnie. Obliczylibyśmy to zatem w następujący sposób:

Odchylenie standardowe = √ (0,3785 + 0,0689 + 0,1059 + 0,2643 + 0,1301) = 0,9734

Wariancja jest po prostu kwadratem odchylenia standardowego, więc:

Odchylenie = 0,9734 ² = 0,9475

Poniższe przykłady pokazują, jak obliczyć odchylenie standardowe rozkładu prawdopodobieństwa w kilku innych scenariuszach.

Przykład 1: Odchylenie standardowe awarii pojazdów

Poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że w danym pojeździe wystąpi określona liczba awarii akumulatora w okresie 10 lat:

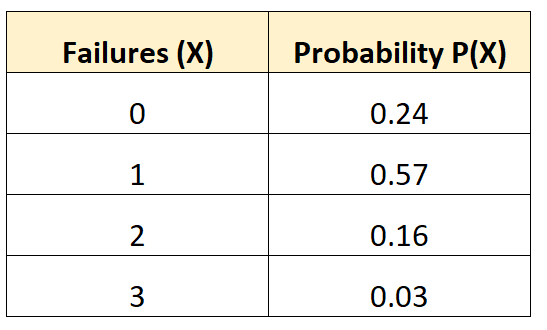
Pytanie: Jakie jest odchylenie standardowe liczby awarii tego pojazdu?

Rozwiązanie: Średnią liczbę oczekiwanych awarii oblicza się w następujący sposób:

μ = 0*0,24 + 1*0,57 + 2*0,16 + 3*0,03 = 0,98 awarii.

Moglibyśmy wówczas obliczyć odchylenie standardowe w następujący sposób:

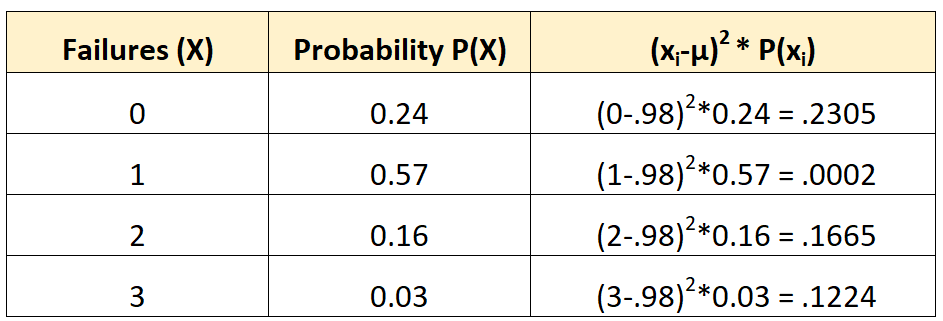
Odchylenie standardowe to pierwiastek kwadratowy z sumy wartości w trzeciej kolumnie. Obliczylibyśmy to zatem w następujący sposób:

Odchylenie standardowe = √ (0,2305 + 0,0002 + 0,1665 + 0,1224) = 0,7208

Przykład 2: Odchylenie standardowe sprzedaży

Poniższy rozkład prawdopodobieństwa informuje nas o prawdopodobieństwie, że dany sprzedawca dokona określonej liczby sprzedaży w nadchodzącym miesiącu:

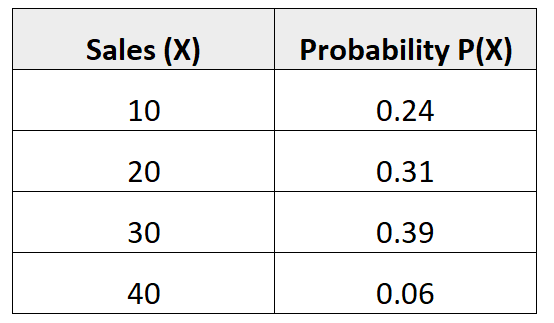
Pytanie: Jakie jest odchylenie standardowe liczby sprzedaży tego sprzedawcy w nadchodzącym miesiącu?

Rozwiązanie: Średnią liczbę oczekiwanych sprzedaży oblicza się w następujący sposób:

μ = 10*0,24 + 20*0,31 + 30*0,39 + 40*0,06 = 22,7 brudny.

Moglibyśmy wówczas obliczyć odchylenie standardowe w następujący sposób:

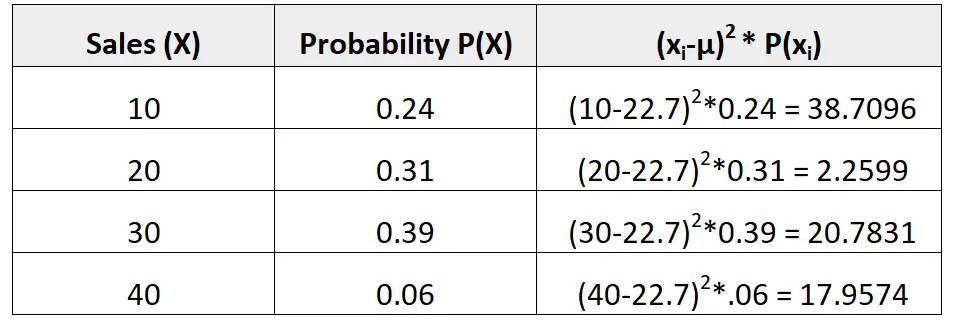
Odchylenie standardowe to pierwiastek kwadratowy z sumy wartości w trzeciej kolumnie. Obliczylibyśmy to zatem w następujący sposób:

Odchylenie standardowe = √ (38,7096 + 2,2599 + 20,7831 + 17,9574) = 8,928

Dodatkowe zasoby

Jak znaleźć średnią rozkładu prawdopodobieństwa
Kalkulator rozkładu prawdopodobieństwa