Randomizacja w statystykach: definicja i przykład
W dziedzinie statystyki randomizacja odnosi się do losowego przydzielania badanych do różnych grup terapeutycznych.
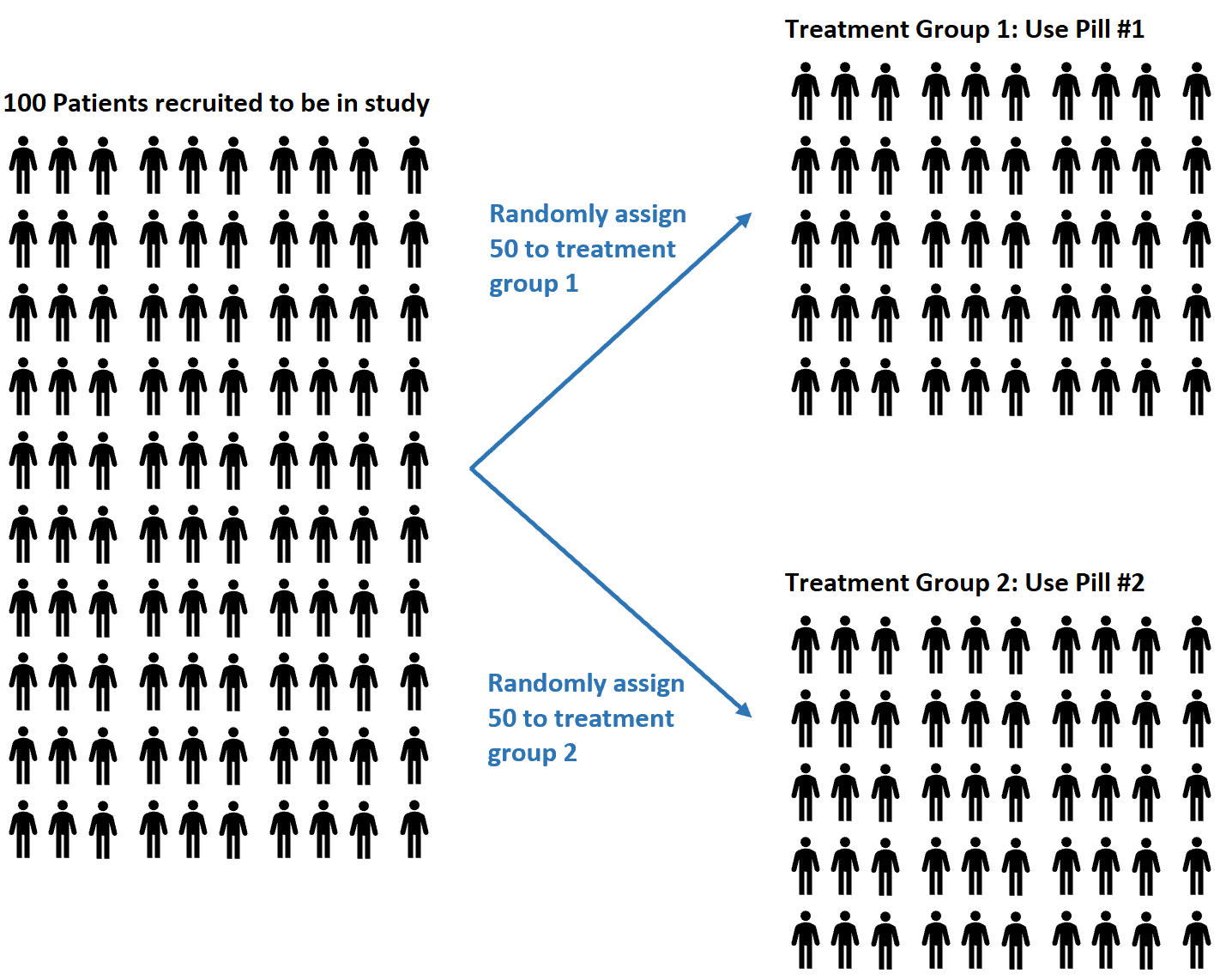
Załóżmy na przykład, że badacze rekrutują 100 osób do udziału w badaniu, w którym mają nadzieję zrozumieć, czy dwie różne pigułki mają różny wpływ na ciśnienie krwi.
Mogą zdecydować się na użycie generatora liczb losowych, aby losowo przypisać każdemu pacjentowi pigułkę nr 1 lub pigułkę nr 2.
Zalety randomizacji
Celem randomizacji jest kontrola zmiennych ukrytych – zmiennych, które nie są bezpośrednio uwzględnione w analizie, ale mimo to w jakiś sposób wpływają na analizę.
Na przykład, jeśli badacze badają wpływ dwóch różnych tabletek na ciśnienie krwi, na analizę mogą mieć wpływ następujące ukryte zmienne:
- Odzież smokingowa
- Dieta
- Ćwiczenia
Losowo przypisując pacjentów do grup terapeutycznych maksymalizujemy szansę, że ukryte zmienne w równym stopniu wpłyną na obie grupy terapeutyczne.
Oznacza to, że każdą różnicę w ciśnieniu krwi można przypisać rodzajowi pigułki, a nie działaniu ukrytej zmiennej.
Blokuj randomizację
Rozszerzenie randomizacji znane jest jako randomizacja blokowa . Jest to proces polegający na pierwszym podzieleniu pacjentów na bloki, a następnie zastosowaniu randomizacji w celu przydzielenia pacjentów w ramach bloków do różnych terapii.
Na przykład, jeśli badacze chcą wiedzieć, czy dwie różne pigułki w różny sposób wpływają na ciśnienie krwi, mogą najpierw podzielić wszystkich pacjentów na dwa bloki w zależności od płci: mężczyzna lub kobieta.
Następnie w każdym bloku mogą zastosować randomizację, aby losowo przypisać pacjentów do stosowania pigułki nr 1 lub pigułki nr 2.
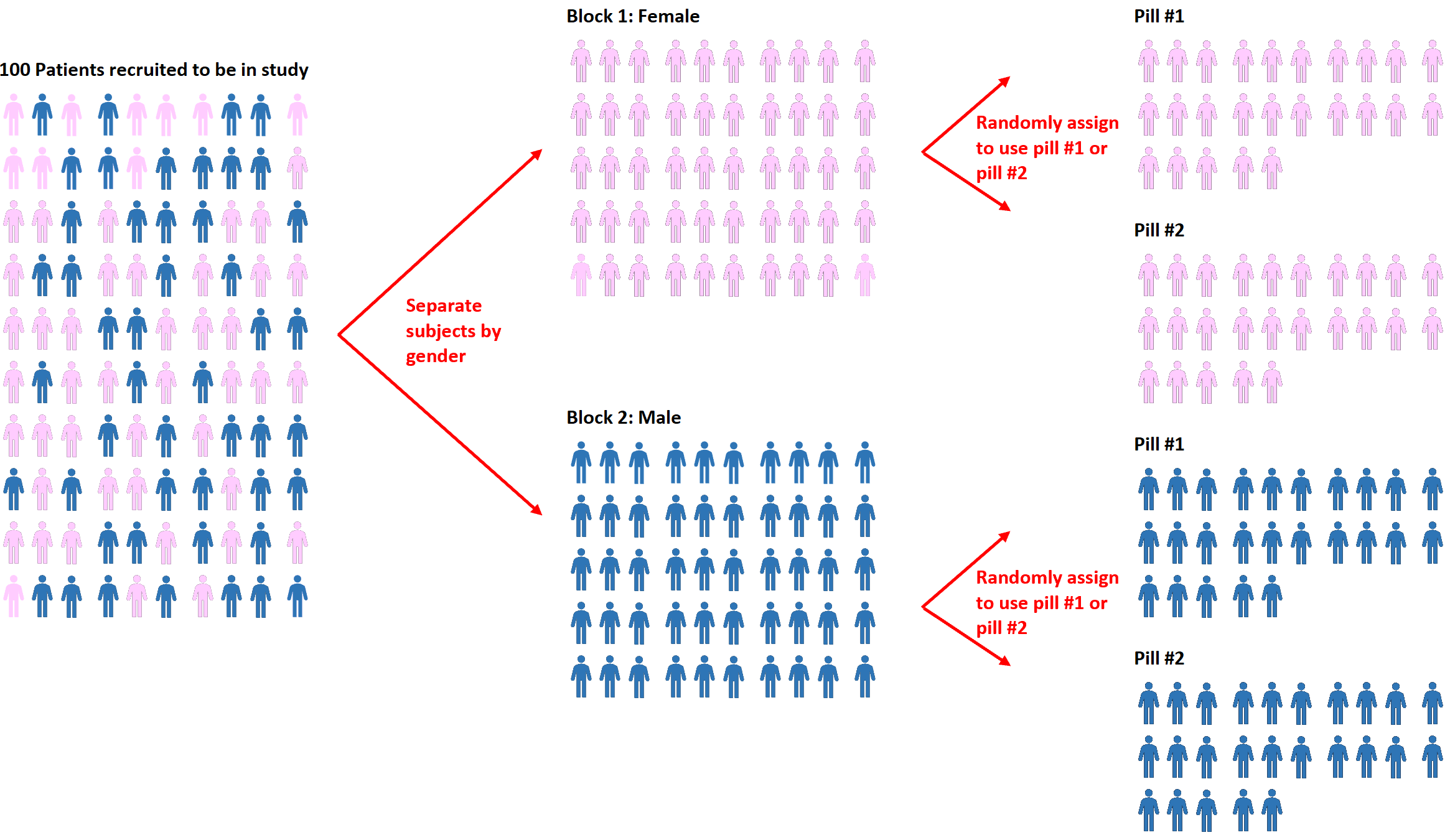
Zaletą tego podejścia jest to, że badacze mogą bezpośrednio kontrolować wpływ płci na ciśnienie krwi, ponieważ wiemy, że mężczyźni i kobiety prawdopodobnie zareagują inaczej na każdą pigułkę.
Wykorzystując płeć jako blokadę, jesteśmy w stanie wyeliminować tę zmienną jako potencjalne źródło zmienności. Jeśli istnieją różnice w ciśnieniu krwi pomiędzy obiema tabletkami, możemy wiedzieć, że płeć nie jest podstawową przyczyną tych różnic.
Dodatkowe zasoby
Blokowanie w statystykach: definicja i przykład
Randomizacja permutowanych bloków: definicja i przykład
Zmienne ukryte: definicja i przykłady