Jak obliczyć błąd standardowy regresji w programie excel

Dopasowujemy model regresji liniowej , model przyjmuje następującą postać:

Y = β ₀ + β ₁ X + … + β _ja

gdzie ϵ jest składnikiem błędu niezależnym od X.

Bez względu na to, jak X można wykorzystać do przewidzenia wartości Y, w modelu zawsze wystąpi błąd losowy.

Jednym ze sposobów pomiaru rozproszenia tego błędu losowego jest użycie błędu standardowego modelu regresji , który jest sposobem pomiaru odchylenia standardowego reszt ϵ.

W tym samouczku przedstawiono krok po kroku przykład obliczania błędu standardowego modelu regresji w programie Excel.

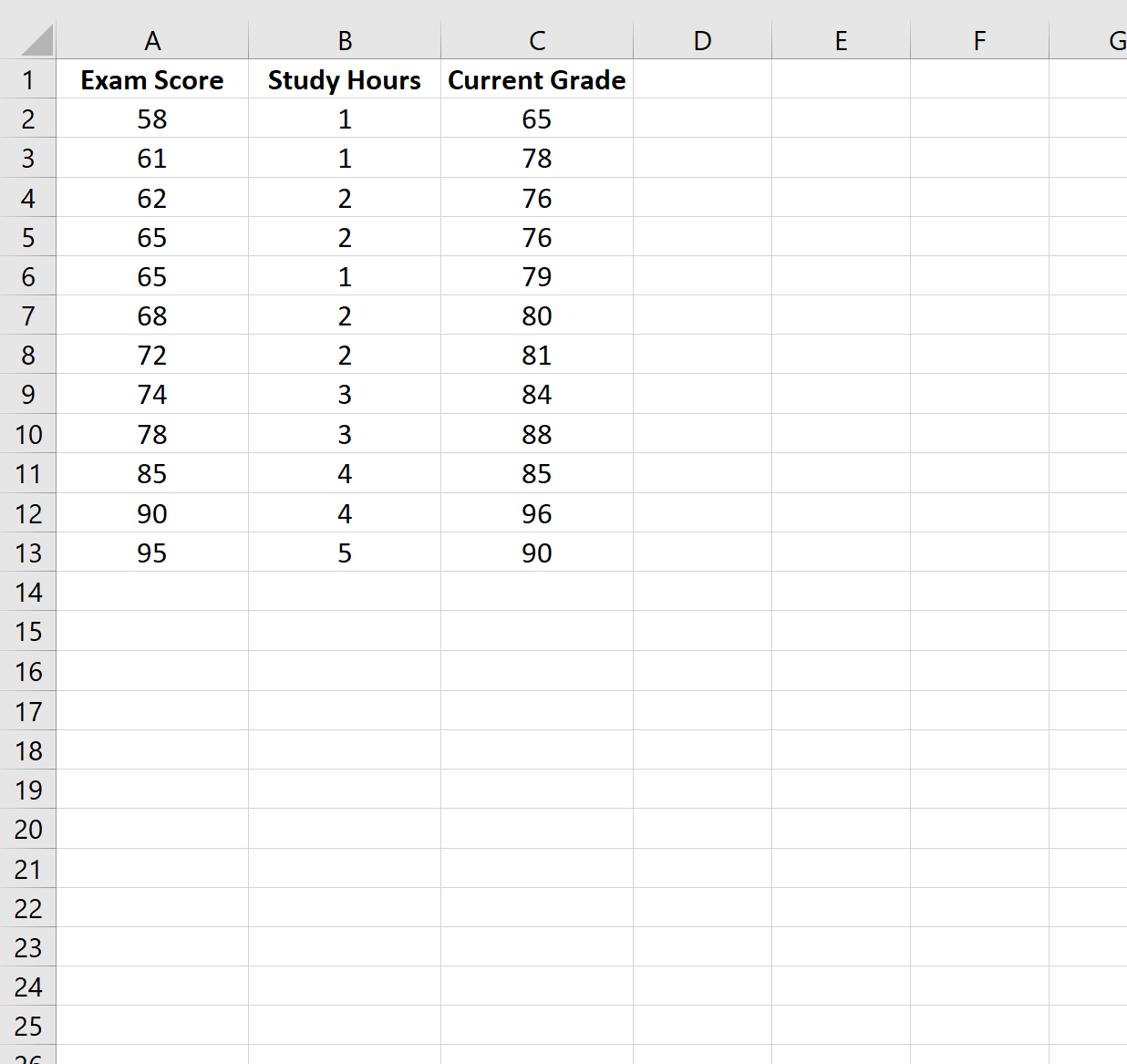
Krok 1: Utwórz dane

Na potrzeby tego przykładu utworzymy zbiór danych zawierający następujące zmienne dla 12 różnych uczniów:

• Wynik egazminu
• Godziny spędzone na nauce
• Aktualna klasa

Krok 2: Dopasuj model regresji

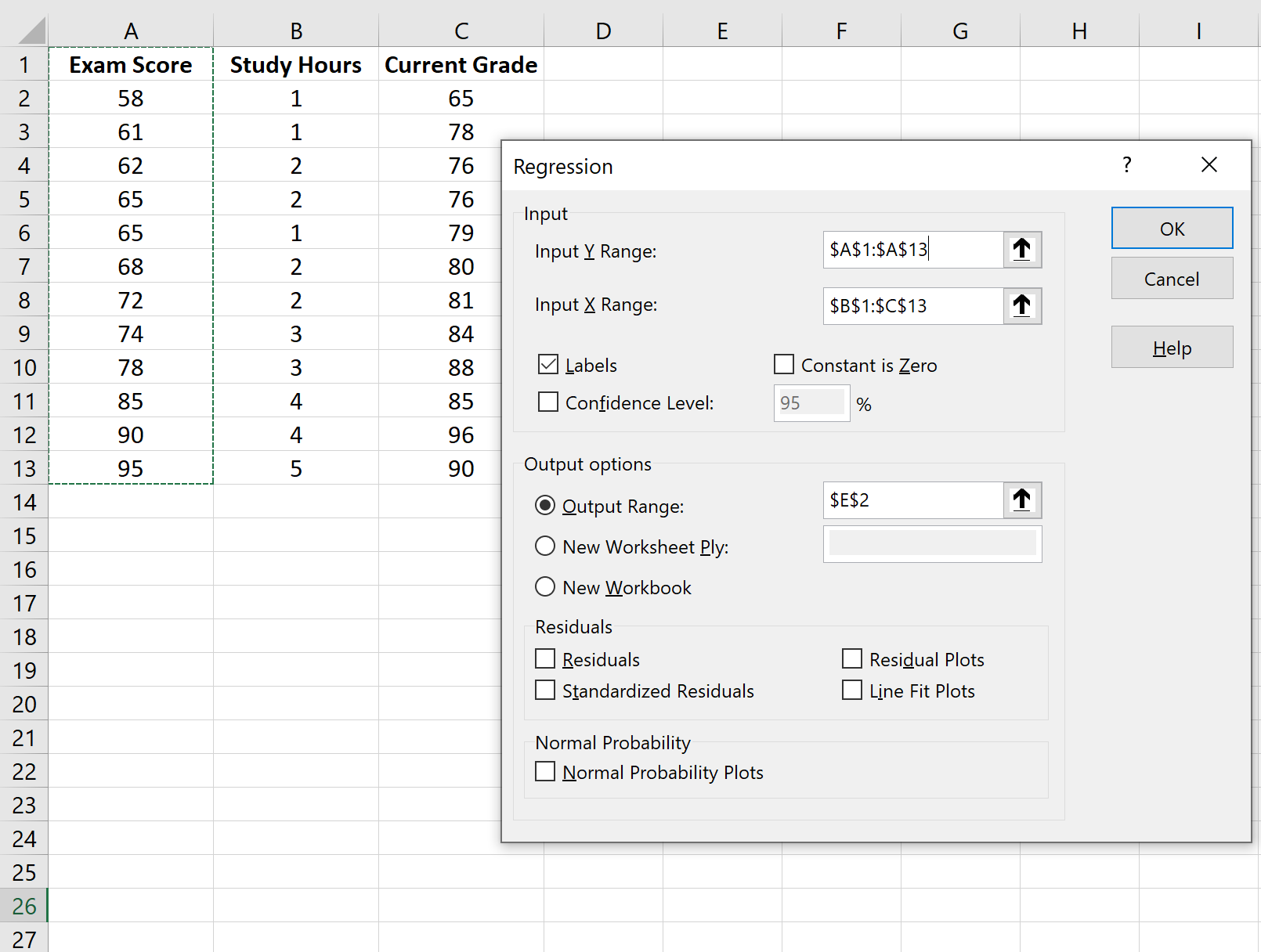
Następnie dopasujemy model regresji liniowej , wykorzystując wynik egzaminu jakozmienną odpowiedzi oraz godziny nauki i aktualną ocenę jako zmienne predykcyjne.

Aby to zrobić, kliknij kartę Dane na górnej wstążce, a następnie kliknij opcję Analiza danych :

Jeśli ta opcja nie jest dostępna, należy najpierw załadować pakiet Data Analysis ToolPak .

W wyświetlonym oknie wybierz Regresja . W nowym oknie, które się pojawi, podaj następujące informacje:

Po kliknięciu OK pojawią się dane wyjściowe modelu regresji:

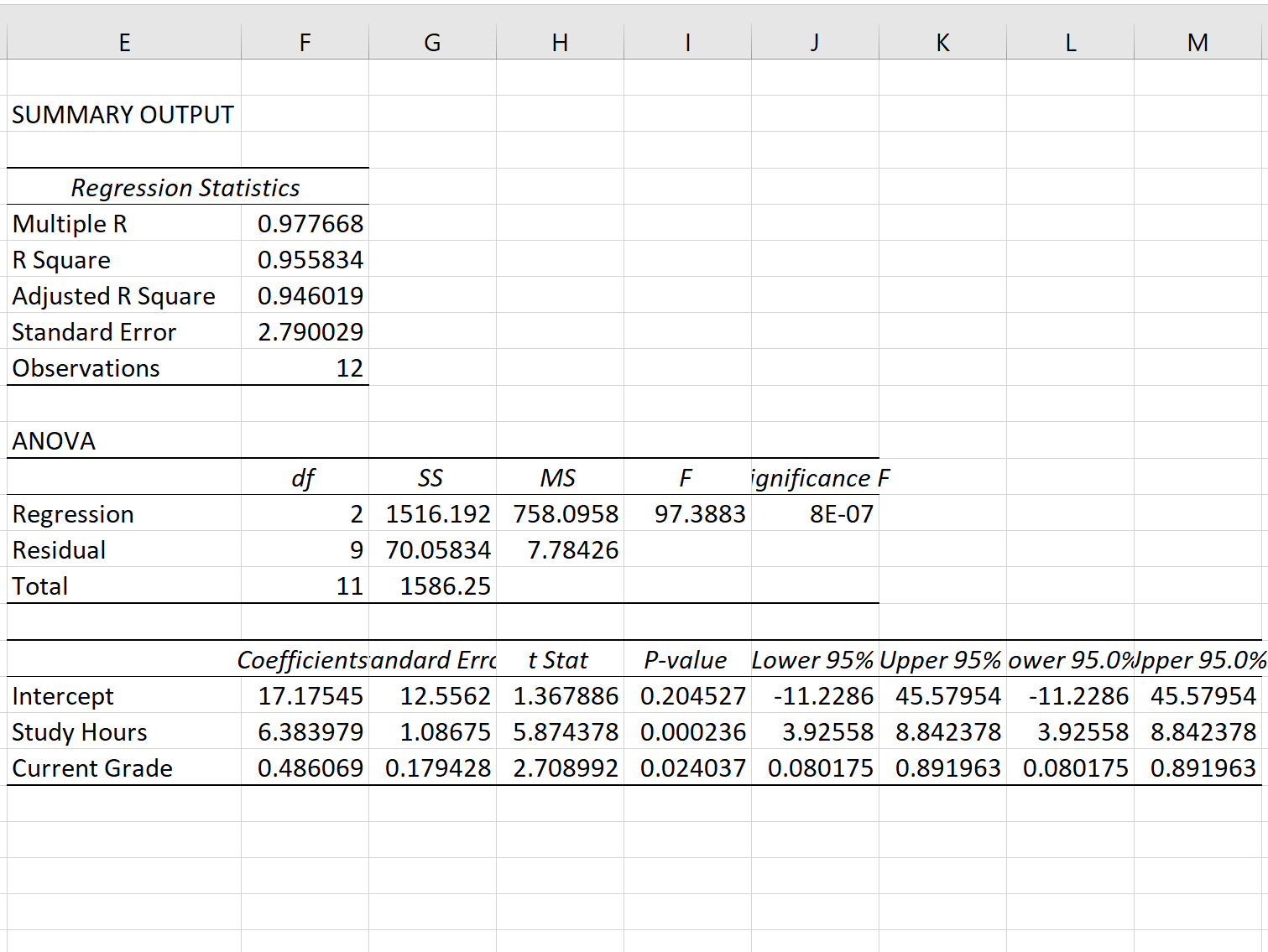
Krok 3: Zinterpretuj błąd standardowy regresji

Błąd standardowy modelu regresji to liczba znajdująca się obok błędu standardowego :

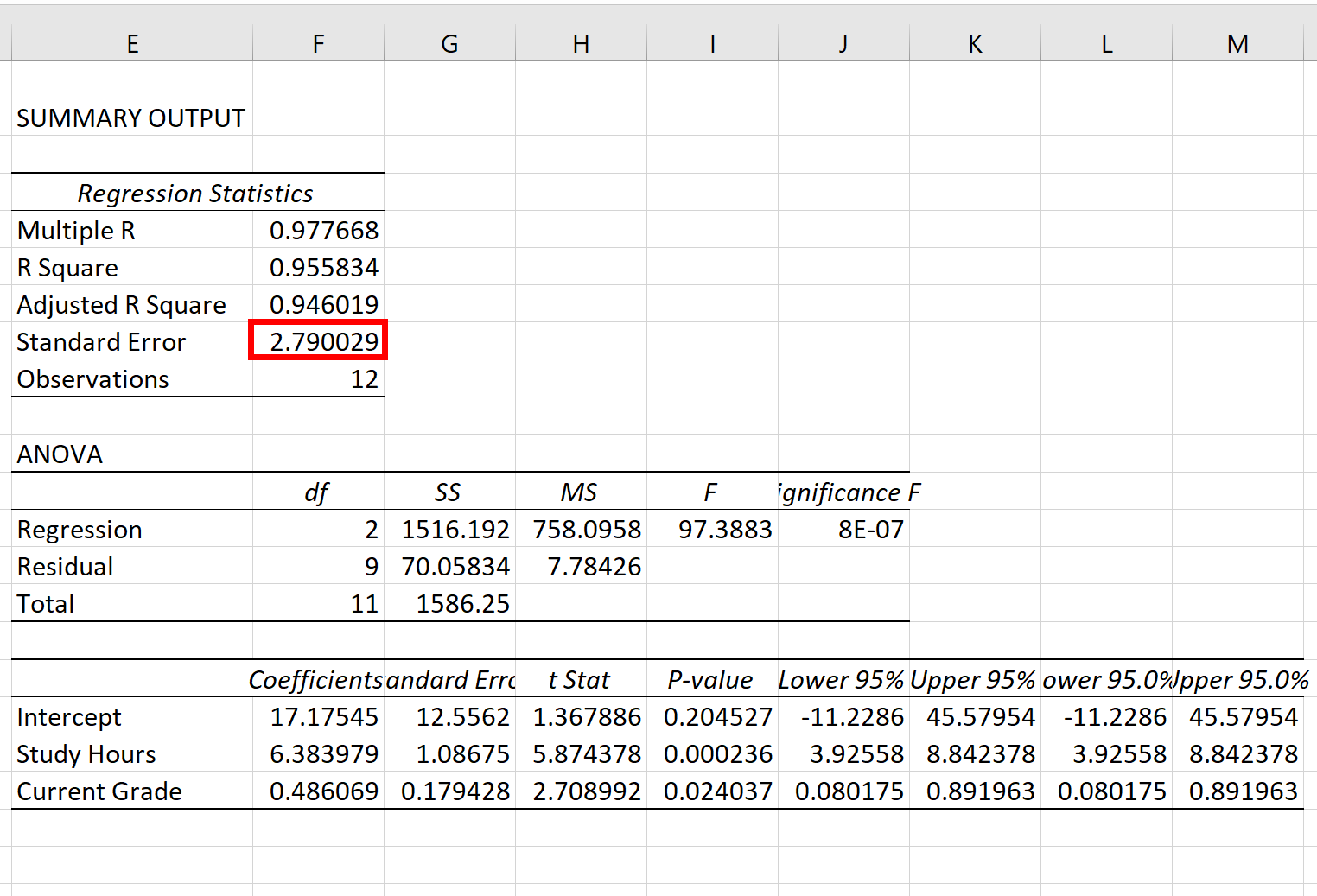
Okazuje się, że błąd standardowy tego konkretnego modelu regresji wynosi 2,790029 .

Liczba ta reprezentuje średnią odległość pomiędzy rzeczywistymi wynikami egzaminu a wynikami egzaminu przewidywanymi przez model.

Należy pamiętać, że niektóre wyniki egzaminów będą odbiegać od przewidywanego wyniku o więcej niż 2,79 jednostki, podczas gdy inne będą bliższe. Jednak średnio odległość między rzeczywistymi wynikami egzaminu a przewidywanymi wynikami wynosi 2,790029 .

Należy również zauważyć, że mniejszy błąd standardowy regresji wskazuje, że model regresji lepiej pasuje do zbioru danych.

Jeśli więc dopasujemy nowy model regresji do zbioru danych i uzyskamy błąd standardowy, powiedzmy, 4,53 , ten nowy model będzie mniej skuteczny w przewidywaniu wyników egzaminów niż poprzedni model.

Dodatkowe zasoby

Innym powszechnym sposobem pomiaru dokładności modelu regresji jest użycie współczynnika R-kwadrat. Sprawdź ten artykuł , aby uzyskać dobre wyjaśnienie korzyści wynikających ze stosowania standardowego błędu regresji do pomiaru dokładności w porównaniu z R-kwadratem.