Jak obliczyć prawdopodobieństwa normalcdf w programie excel

Funkcji NormalCDF w kalkulatorze TI-83 lub TI-84 można użyć do obliczenia prawdopodobieństwa, że zmienna losowa o rozkładzie normalnym przyjmie wartość z określonego zakresu.

W kalkulatorze TI-83 lub TI-84 funkcja ta wykorzystuje następującą składnię

normalcdf (dolny, górny, μ, σ)

Złoto:

• dolna = dolna wartość zakresu
• górna = górna wartość zakresu
• μ = średnia populacji
• σ = odchylenie standardowe populacji

Załóżmy na przykład, że zmienna losowa marozkład normalny ze średnią 50 i odchyleniem standardowym 4. Prawdopodobieństwo, że zmienna losowa przyjmie wartość z zakresu od 48 do 52, można obliczyć w następujący sposób:

normalcdf(48, 52, 50, 4) = 0,3829

Możemy odtworzyć tę odpowiedź w programie Excel za pomocą funkcji ROZKŁ.NORMALNY() , która wykorzystuje następującą składnię:

ROZKŁAD NORMALNY(x, σ, μ, skumulowany)

Złoto:

• x = indywidualna wartość danych
• μ = średnia populacji
• σ = odchylenie standardowe populacji
• skumulowany = FAŁSZ oblicz PDF; TRUE oblicza CDF

Poniższe przykłady pokazują, jak w praktyce wykorzystać tę funkcję.

Przykład 1: Prawdopodobieństwo między dwiema wartościami

Załóżmy, że zmienna losowa ma rozkład normalny ze średnią 50 i odchyleniem standardowym 4. Prawdopodobieństwo, że zmienna losowa przyjmie wartość z zakresu od 48 do 52, można obliczyć w następujący sposób:

 =NORM. DIST (52, 50, 4, TRUE ) - NORM. DIST (48, 50, 4, TRUE )

Poniższy obraz pokazuje, jak wykonać to obliczenie w programie Excel:

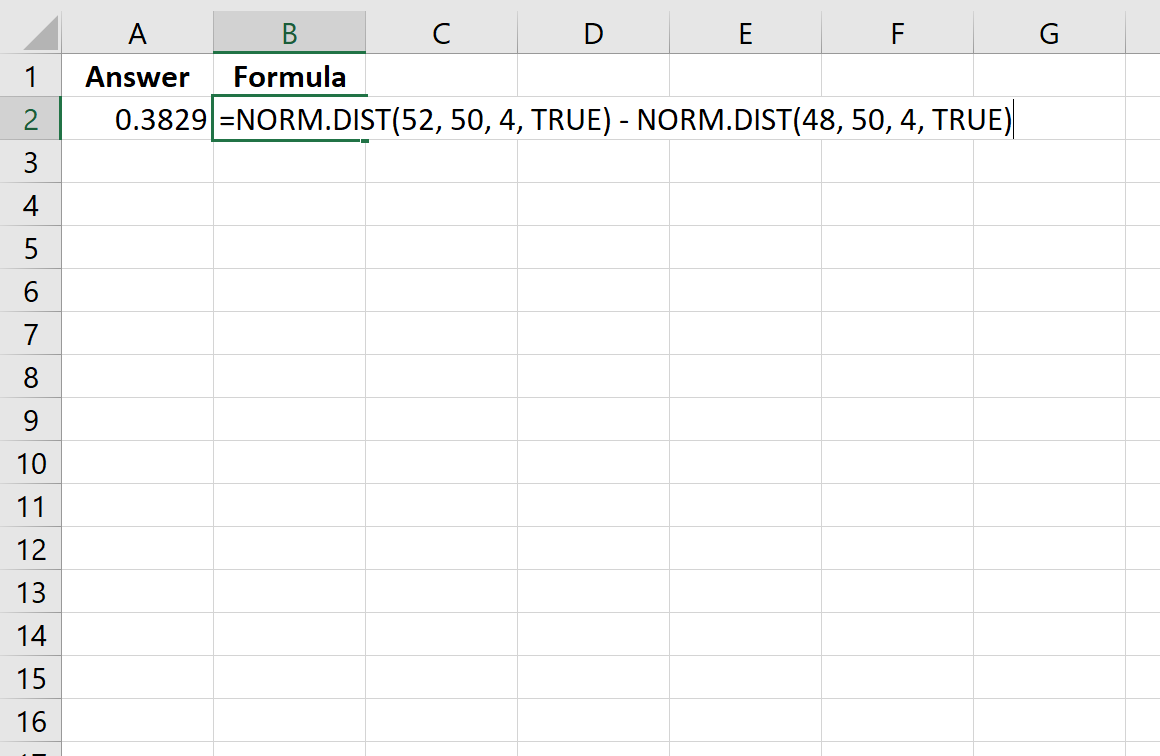
Prawdopodobieństwo wynosi 0,3829.

Przykład 2: Prawdopodobieństwo mniejsze niż jedna wartość

Załóżmy, że zmienna losowa ma rozkład normalny ze średnią 50 i odchyleniem standardowym 4. Prawdopodobieństwo, że zmienna losowa przyjmie wartość mniejszą niż 48, można obliczyć w następujący sposób:

 =NORM. DIST (48, 50, 4, TRUE )

Poniższy obraz pokazuje, jak wykonać to obliczenie w programie Excel:

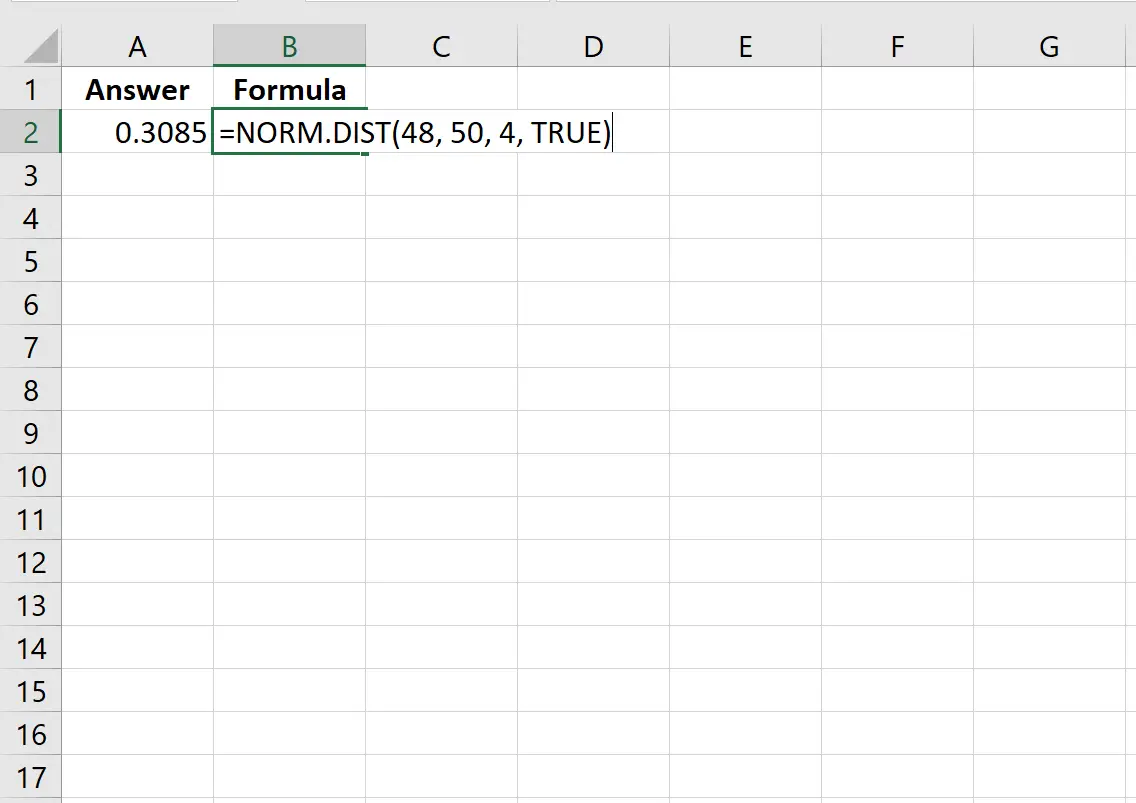
Prawdopodobieństwo wynosi 0,3085.

Przykład 3: Prawdopodobieństwo większe niż wartość

Załóżmy, że zmienna losowa ma rozkład normalny ze średnią 50 i odchyleniem standardowym 4. Prawdopodobieństwo, że zmienna losowa przyjmie wartość większą niż 55, można obliczyć w następujący sposób:

 =1 - NORM. DIST (55, 50, 4, TRUE )

Poniższy obraz pokazuje, jak wykonać to obliczenie w programie Excel:

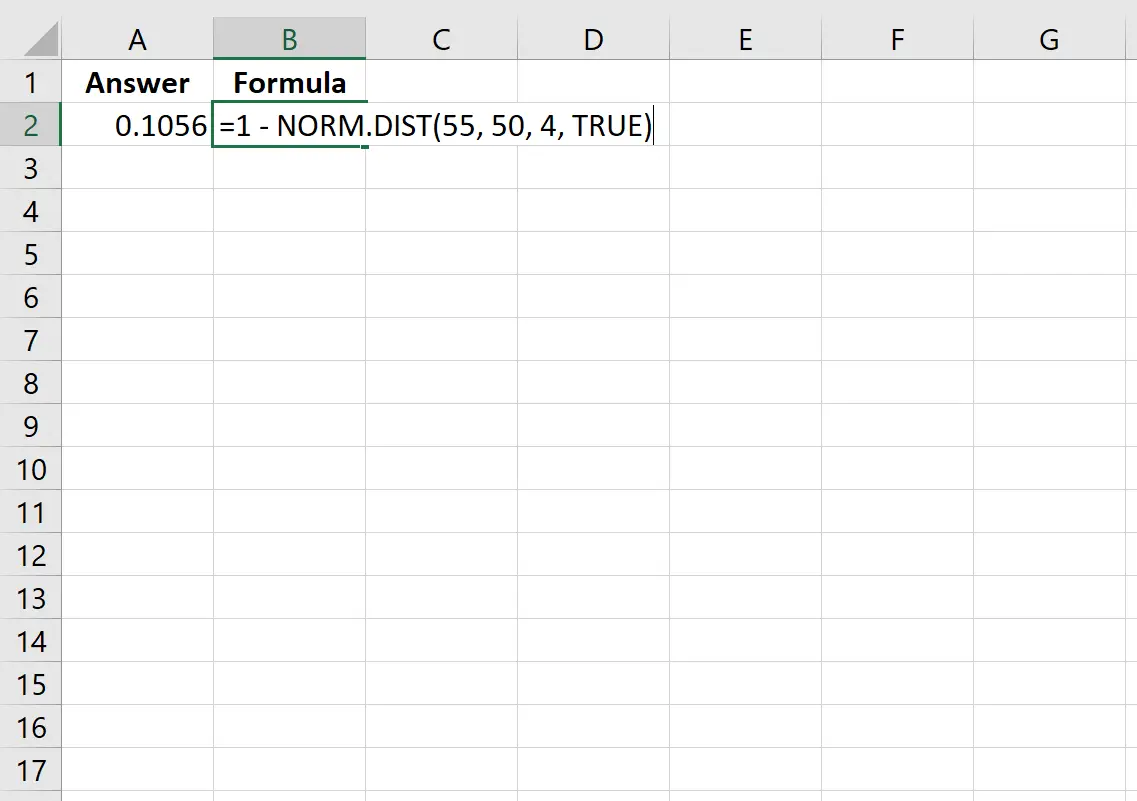
Prawdopodobieństwo wynosi 0,1056.

Dodatkowe zasoby

Możesz także użyć tego normalnego kalkulatora CDF , aby automatycznie znaleźć prawdopodobieństwa związane z rozkładem normalnym.