Jak wykonać korektę bonferroniego w programie excel
Korekta Bonferroniego odnosi się do procesu dostosowywania poziomu alfa (α) dla rodziny testów statystycznych w celu kontrolowania prawdopodobieństwa popełnienia błędu I rodzaju.
Wzór na poprawkę Bonferroniego jest następujący:
α nowy = α oryginał / rz
Złoto:
- oryginalny α: Oryginalny poziom α
- n: Całkowita liczba przeprowadzonych porównań lub testów
Na przykład, jeśli przeprowadzamy trzy testy statystyczne na raz i chcemy zastosować α = 0,05 w każdym teście, poprawka Bonferroniego mówi nam, że powinniśmy zastosować α nowy = 0,01667 .
nowy α = oryginalny α / n = 0,05 / 3 = 0,01667
Zatem powinniśmy odrzucić hipotezę zerową każdego pojedynczego testu tylko wtedy, gdy wartość p testu jest mniejsza niż 0,01667.
Tego typu korektę często przeprowadza się w testach post-hoc po przeprowadzeniu analizy ANOVA, gdy chcemy porównać jednocześnie kilka średnich grupowych.
Poniższy przykład pokazuje krok po kroku, jak przeprowadzić poprawkę Bonferroniego po jednokierunkowej ANOVA w programie Excel.
Krok 1: Utwórz dane
Najpierw utwórzmy fałszywy zbiór danych przedstawiający wyniki uczniów, którzy przygotowali się do egzaminu, stosując jedną z trzech różnych technik uczenia się:
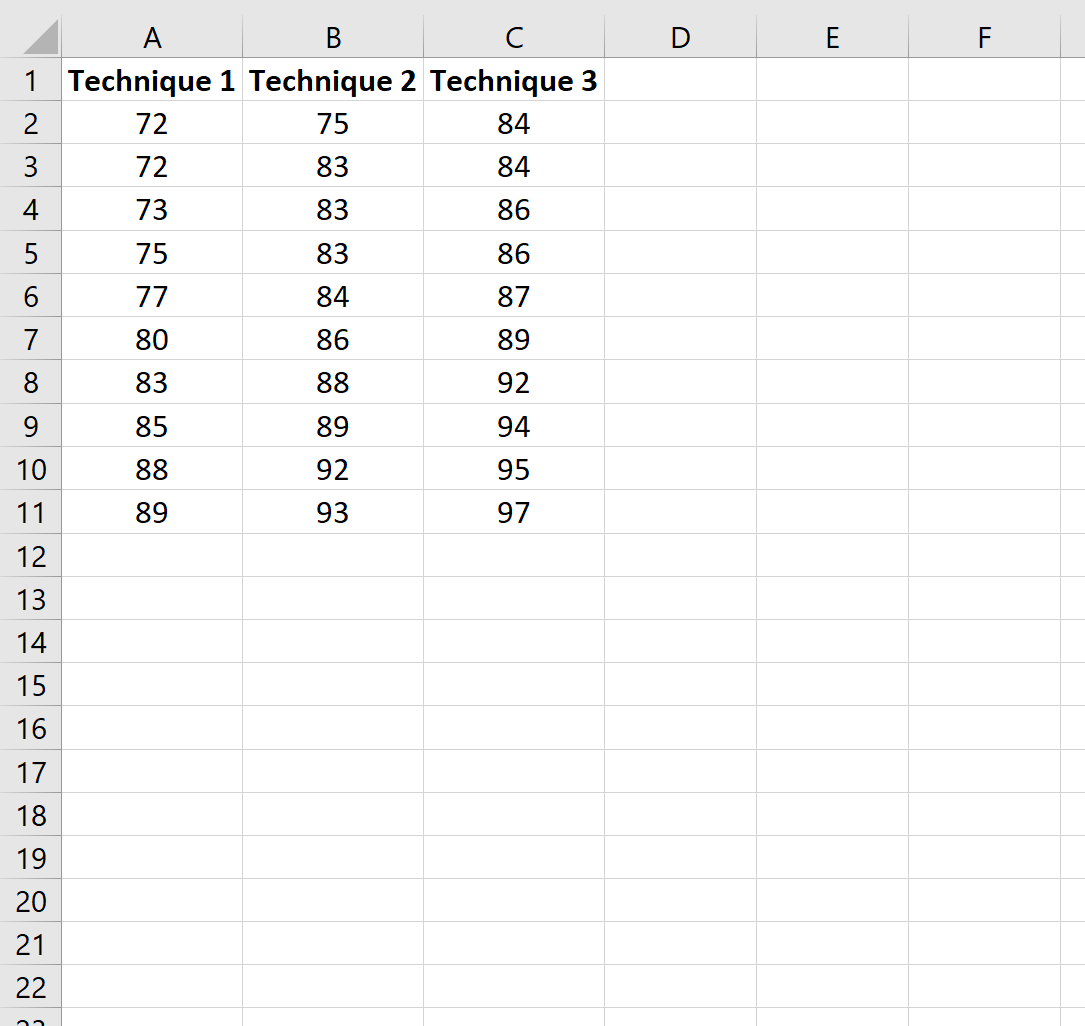
Krok 2: Wykonaj jednokierunkową ANOVA
Następnie przeprowadźmy jednoczynnikową analizę ANOVA, aby ustalić, czy średnie wyniki egzaminu są równe w trzech grupach.
Najpierw zaznacz wszystkie dane, w tym nagłówki kolumn:
Następnie kliknij kartę Dane na górnej wstążce, a następnie kliknij opcję Analiza danych :

Jeśli ta opcja nie jest dostępna, należy najpierw załadować pakiet Analysis ToolPak .
W wyświetlonym oknie kliknij Anova: Single Factor , a następnie kliknij OK .
Podaj następujące informacje, a następnie kliknij OK :
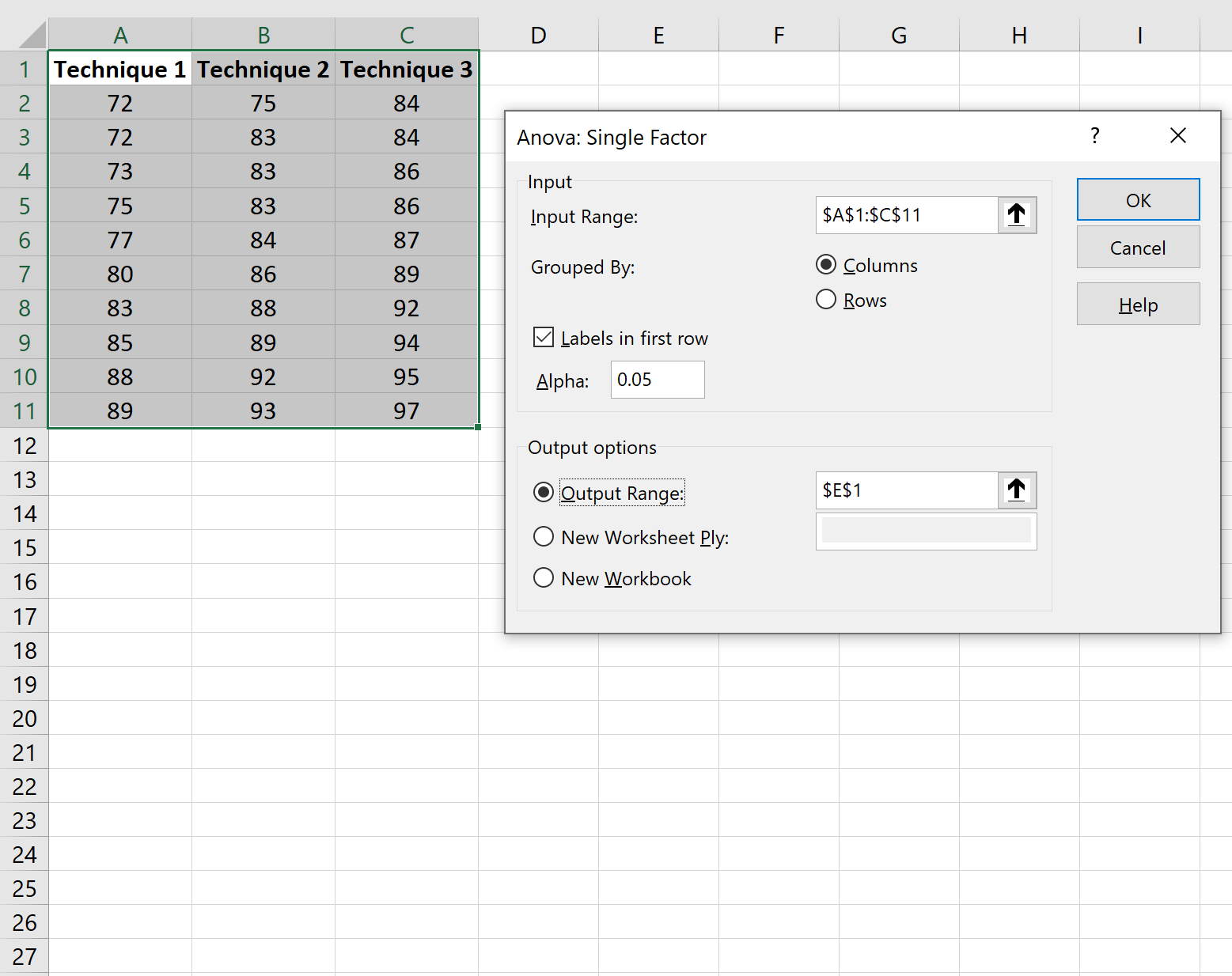
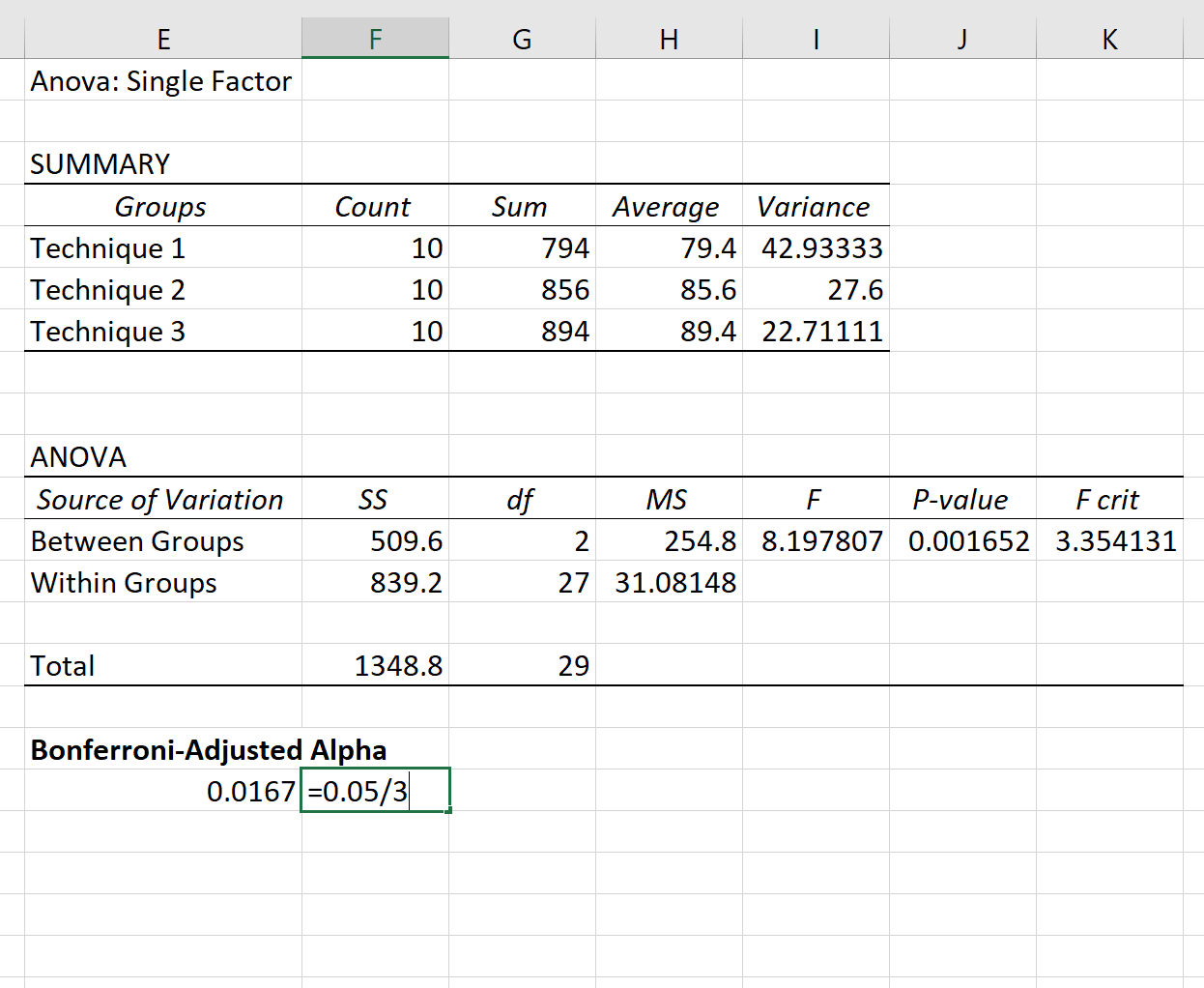
Jednokierunkowe wyniki ANOVA pojawią się automatycznie:
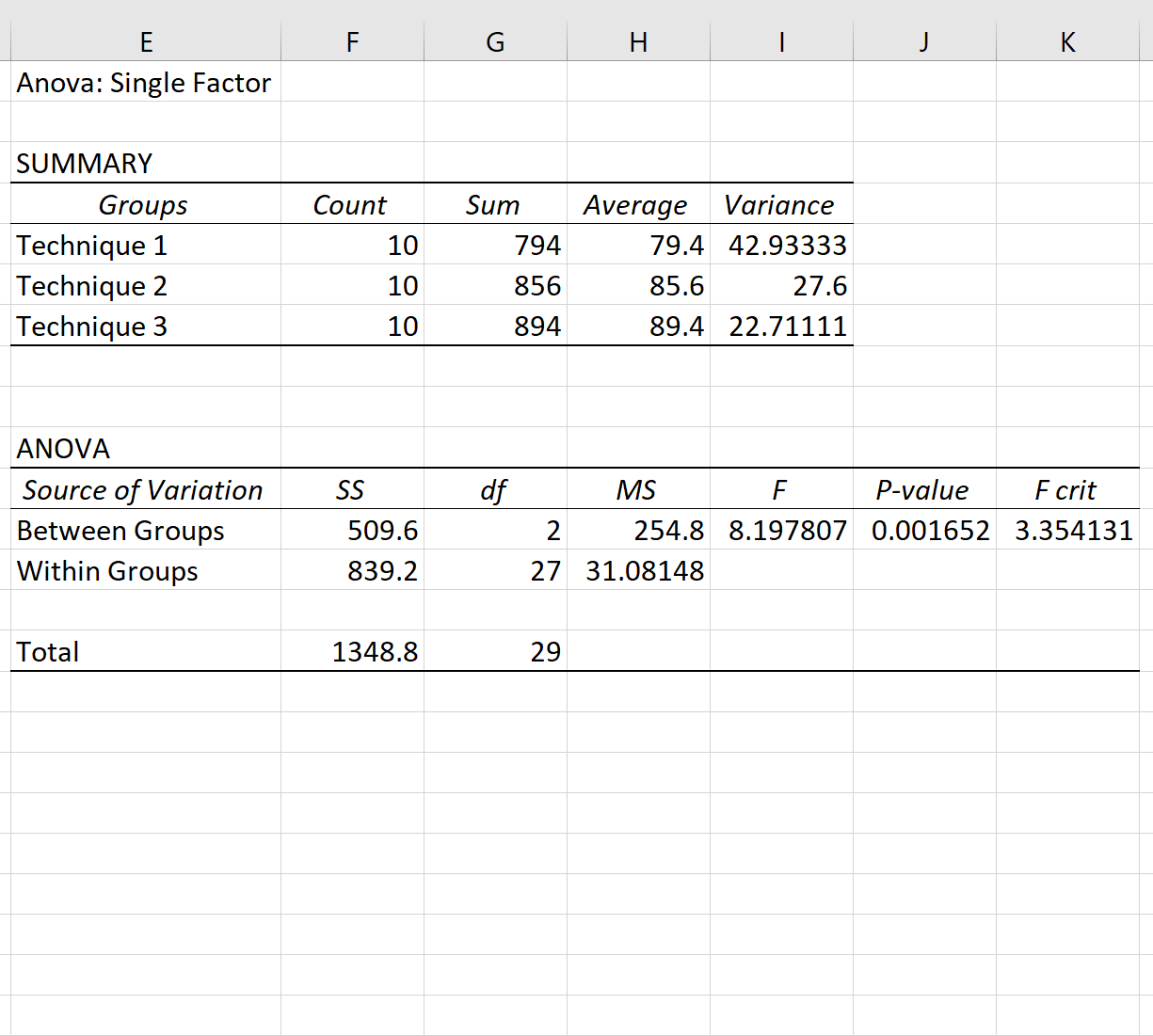
Przypomnijmy, że jednokierunkowa ANOVA ma następujące hipotezy zerowe i alternatywne:
- H 0 (hipoteza zerowa): wszystkie średnie grupowe są równe.
- HA (hipoteza alternatywna): Co najmniej jedna średnia grupowa jest inna odpoczynek.
Ponieważ wartość p w tabeli ANOVA (0,001652) jest mniejsza niż 0,05, mamy wystarczające dowody, aby odrzucić hipotezę zerową. Innymi słowy, średnie wyniki egzaminów w trzech grupach nie są równe.
Następnie możemy dokonać kilku porównań, korzystając z poprawki Bonferroniego, pomiędzy trzema grupami, aby dokładnie zobaczyć, które średnie grupowe są różne.
Krok 3: Wykonaj wielokrotne porównania, korzystając z poprawki Bonferroniego
Korzystając z poprawki Bonferroniego, możemy obliczyć skorygowany poziom alfa w następujący sposób:
α nowy = α oryginał / rz
W naszym przykładzie przeprowadzimy trzy następujące porównania:
- Technika 1 kontra technika 2
- Technika 1 kontra technika 3
- Technika 2 kontra technika 3
Ponieważ w każdym teście chcemy zastosować α = 0,05, poprawka Bonferroniego mówi nam, że powinniśmy zastosować α nowy = 0,0167 .
Następnie użyjemy testu t, aby porównać średnie między każdą grupą. W Excelu możesz użyć następującej składni:
=TEST(Tabela1, Tabela2, kolejki=2, typ=2)
Złoto:
- Tablica1: pierwsza tablica danych
- Tablica2: druga tablica danych
- ogony: liczba ogonów w teście. Będziemy używać „2”, aby wskazać test dwustronny.
- type: typ testu t do wykonania. Użyjemy „2”, aby wskazać test t z równymi wariancjami.
Poniższy zrzut ekranu pokazuje, jak wykonać każdy test t:
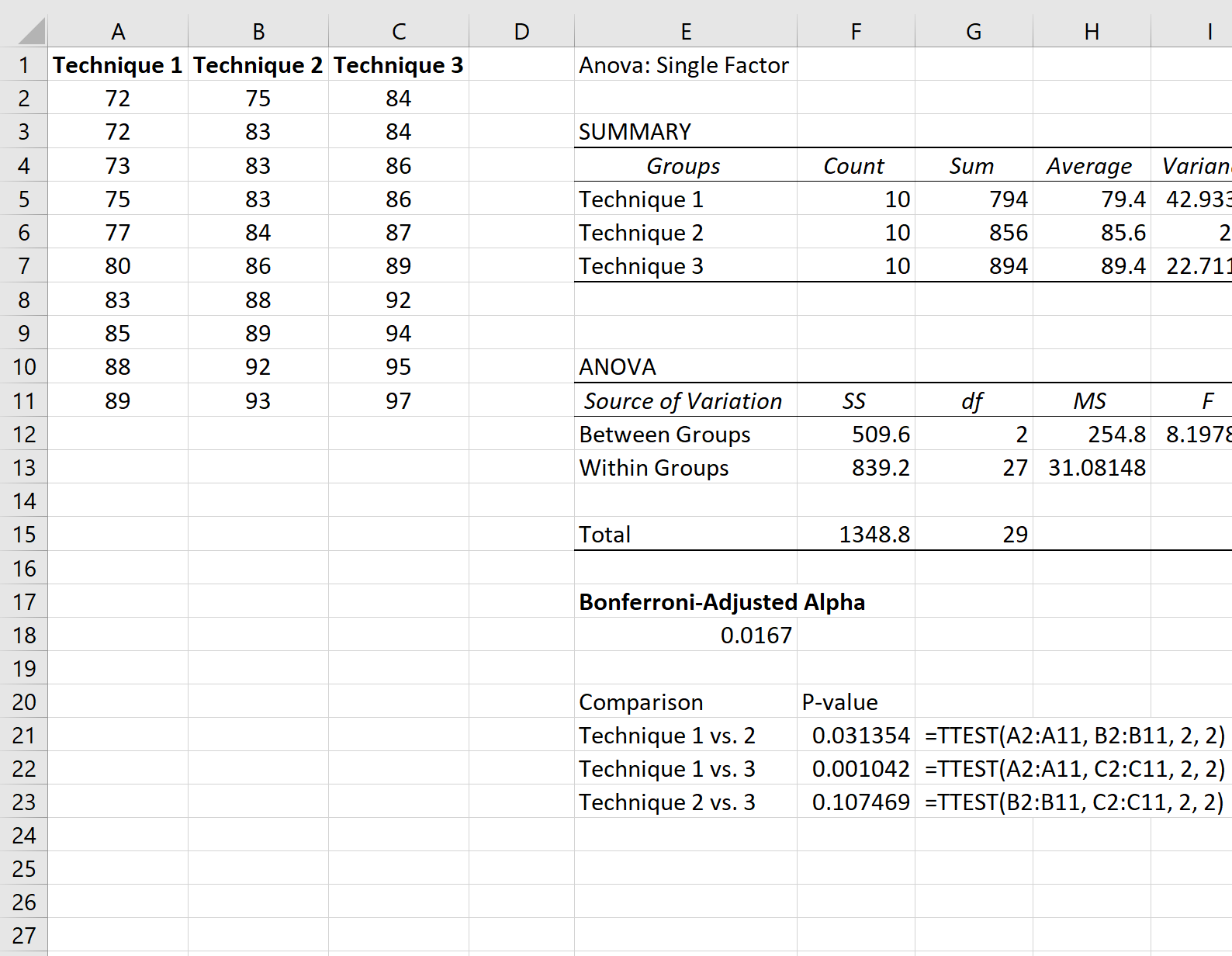
Jedyna wartość p poniżej poziomu alfa skorygowanego przez Bonferroniego pochodzi z porównania techniki 1 i techniki 2, dla której wartość p wynosiła 0,001042 .
Można zatem stwierdzić, że jedynie statystycznie istotna różnica w średnich wynikach egzaminu występowała pomiędzy Techniką 1 i Techniką 2.
Dodatkowe zasoby
Jaki jest poziom błędu na rodzinę?
Poprawka Bonferroniego: definicja i przykład
Kalkulator korekcji Bonferroniego