Skorygowany iloraz szans: definicja + przykłady

W statystyce iloraz szans informuje nas o stosunku prawdopodobieństwa wystąpienia zdarzenia w grupie badanej do prawdopodobieństwa wystąpienia zdarzenia w grupie kontrolnej.

Iloraz szans najczęściej pojawia się w regresji logistycznej , która jest metodą, której używamy do dopasowania modelu regresji, który ma jedną lub więcej zmiennych predykcyjnych i binarną zmienną odpowiedzi.

Skorygowany iloraz szans to iloraz szans skorygowany o inne zmienne predykcyjne w modelu.

Jest to szczególnie przydatne, gdy pomaga nam zrozumieć, w jaki sposób zmienna predykcyjna wpływa na prawdopodobieństwo wystąpienia zdarzenia, po uwzględnieniu wpływu innych zmiennych predykcyjnych.

Poniższy przykład ilustruje różnicę między ilorazem szans a skorygowanym ilorazem szans.

Przykład: Obliczanie skorygowanych ilorazów szans

Załóżmy, że chcemy zrozumieć, czy wiek matki wpływa na prawdopodobieństwo urodzenia dziecka z niską masą urodzeniową.

Aby to zbadać, możemy przeprowadzić regresję logistyczną, wykorzystując wiek jako zmienną predykcyjną i niską masę urodzeniową (tak lub nie) jakozmienną odpowiedzi .

Załóżmy, że zbieramy dane dotyczące 300 matek i dopasowujemy model regresji logistycznej. Oto wyniki:

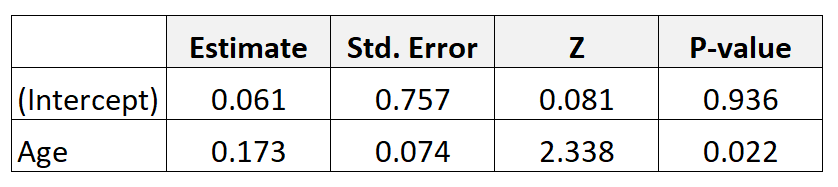
Aby otrzymać iloraz szans dla wieku, po prostu potęguj oszacowanie współczynnika z tabeli: e ^0,173 = 1,189 .

To mówi nam, że zwiększenie wieku o jeden rok wiąże się ze wzrostem o 1189 szans na urodzenie dziecka z niską masą urodzeniową. Innymi słowy, szanse na urodzenie dziecka z niską masą urodzeniową zwiększają się o 18,9% z każdym dodatkowym rocznym wzrostem wieku.

Ten iloraz szans nazywany jest „surowym” ilorazem szans lub „nieskorygowanym” ilorazem szans, ponieważ nie został skorygowany o inne zmienne predykcyjne w modelu, ponieważ jest jedyną zmienną predykcyjną w modelu.

Załóżmy jednak, że chcemy zrozumieć, czy wiek matki i nawyki palenia wpływają na prawdopodobieństwo urodzenia dziecka z niską masą urodzeniową.

Aby to zbadać, możemy przeprowadzić regresję logistyczną, wykorzystując wiek i palenie (tak lub nie) jako zmienne predykcyjne oraz niską masę urodzeniową jakozmienną odpowiedzi .

Załóżmy, że zbieramy dane dotyczące 300 matek i dopasowujemy model regresji logistycznej. Oto wyniki:

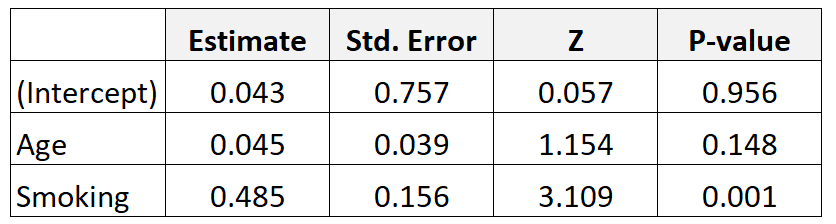
Oto jak interpretować wyniki:

Wiek: Iloraz szans skorygowany o wiek oblicza się w następujący sposób: e ^0,045 = 1,046 . Oznacza to, że szanse na urodzenie dziecka z niską masą urodzeniową zwiększają się o 4,6% na każdy dodatkowy roczny wzrost wieku, przy założeniu, że zmienna palenia pozostaje stała.

Załóżmy na przykład, że matka A i matka B palą. Jeśli matka A jest o rok starsza od matki B, wówczas prawdopodobieństwo, że matka A urodzi dziecko z niską masą urodzeniową, jest 1,046 razy większe niż prawdopodobieństwo, że matka B urodzi dziecko z niską masą urodzeniową.

Palenie : Skorygowany iloraz szans dla palenia oblicza się w następujący sposób: ^e,485 = 1,624 . Oznacza to, że szanse na urodzenie dziecka z niską masą urodzeniową zwiększają się o 62,4%, jeśli matka pali (w porównaniu do osób niepalących), przy założeniu, że zmienna wieku pozostaje stała.

Załóżmy na przykład, że matka A i matka B mają po 30 lat. Jeśli matka A pali w czasie ciąży, a matka B nie pali, wówczas ryzyko, że matka A urodzi dziecko z niską masą urodzeniową, jest o 62,4% większe niż ryzyko, że matka B urodzi dziecko z niską masą urodzeniową.

Należy pamiętać, że iloraz szans skorygowany o wiek jest niższy niż iloraz szans nieskorygowany z poprzedniego przykładu. Dzieje się tak dlatego, że gdy inne zmienne predykcyjne zwiększają prawdopodobieństwo wystąpienia zmiennej odpowiedzi, skorygowany iloraz szans dla zmiennej predykcyjnej już obecnej w modelu zawsze będzie się zmniejszał.

Podsumowanie: iloraz szans w porównaniu ze skorygowanym ilorazem szans

Iloraz szans (czasami nazywany „przybliżonym” ilorazem szans) jest przydatny, gdy informuje nas, jak zmiany zmiennej predykcyjnej wpływają na prawdopodobieństwo wystąpienia zmiennej odpowiedzi.

Skorygowany iloraz szans jest przydatny, gdy informuje nas, jak zmiany zmiennej predykcyjnej wpływają na prawdopodobieństwo wystąpienia zmiennej odpowiedzi, po uwzględnieniu innych zmiennych predykcyjnych w modelu.

Dodatkowe zasoby

Wprowadzenie do regresji logistycznej
Jak przeprowadzić regresję logistyczną w R
Jak przeprowadzić regresję logistyczną w Pythonie