Jak obliczyć współczynnik korelacji wewnątrzklasowej w programie excel

Współczynnik korelacji wewnątrzklasowej (ICC) służy do określenia, czy pozycje (lub tematy) mogą być wiarygodnie ocenione przez różnych oceniających.

Wartość ICC może mieścić się w przedziale od 0 do 1, gdzie 0 oznacza brak wiarygodności wśród oceniających, a 1 oznacza doskonałą niezawodność.

W tym samouczku przedstawiono krok po kroku przykład obliczenia ICC w programie Excel.

Krok 1: Utwórz dane

Załóżmy, że czterech różnych sędziów zostaje poproszonych o ocenę jakości 10 różnych egzaminów wstępnych na studia. Wyniki przedstawiono poniżej:

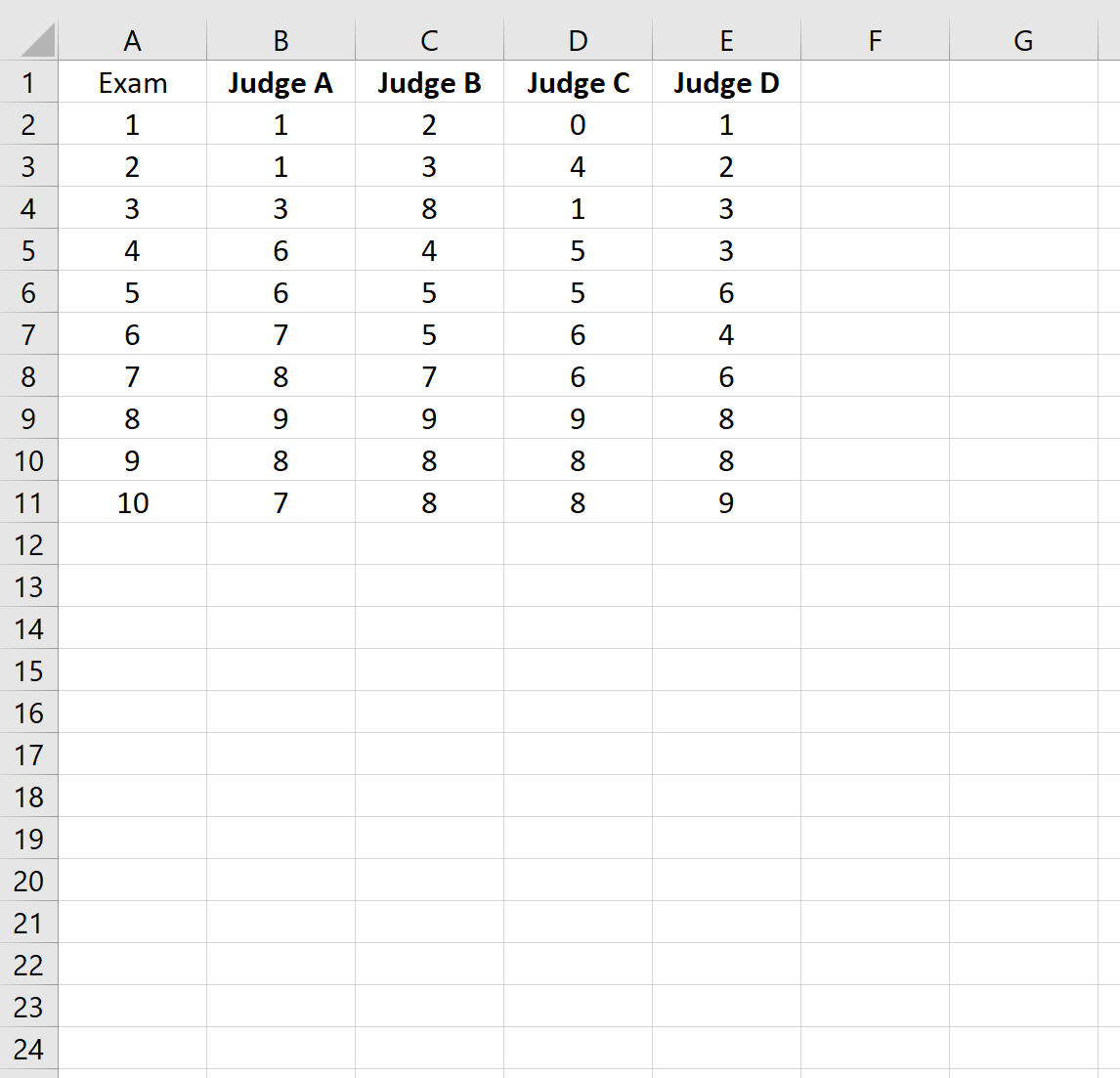
Krok 2: Dopasuj ANOVA

Aby obliczyć ICC dla tych ocen, musimy najpierw dopasować Anova: dwuczynnikowy bez replikacji .

Aby to zrobić, zaznacz komórki A1:E11 w następujący sposób:

Aby to zrobić, kliknij kartę Dane na górnej wstążce, a następnie kliknij opcję Analiza danych w grupie Analiza :

Jeśli ta opcja nie jest dostępna, należy najpierw załadować pakiet Analysis ToolPak .

W wyświetlonym menu rozwijanym kliknij Anova: Two-Factor Without Replication , a następnie kliknij OK . W nowym oknie, które się pojawi, podaj następujące informacje, a następnie kliknij OK :

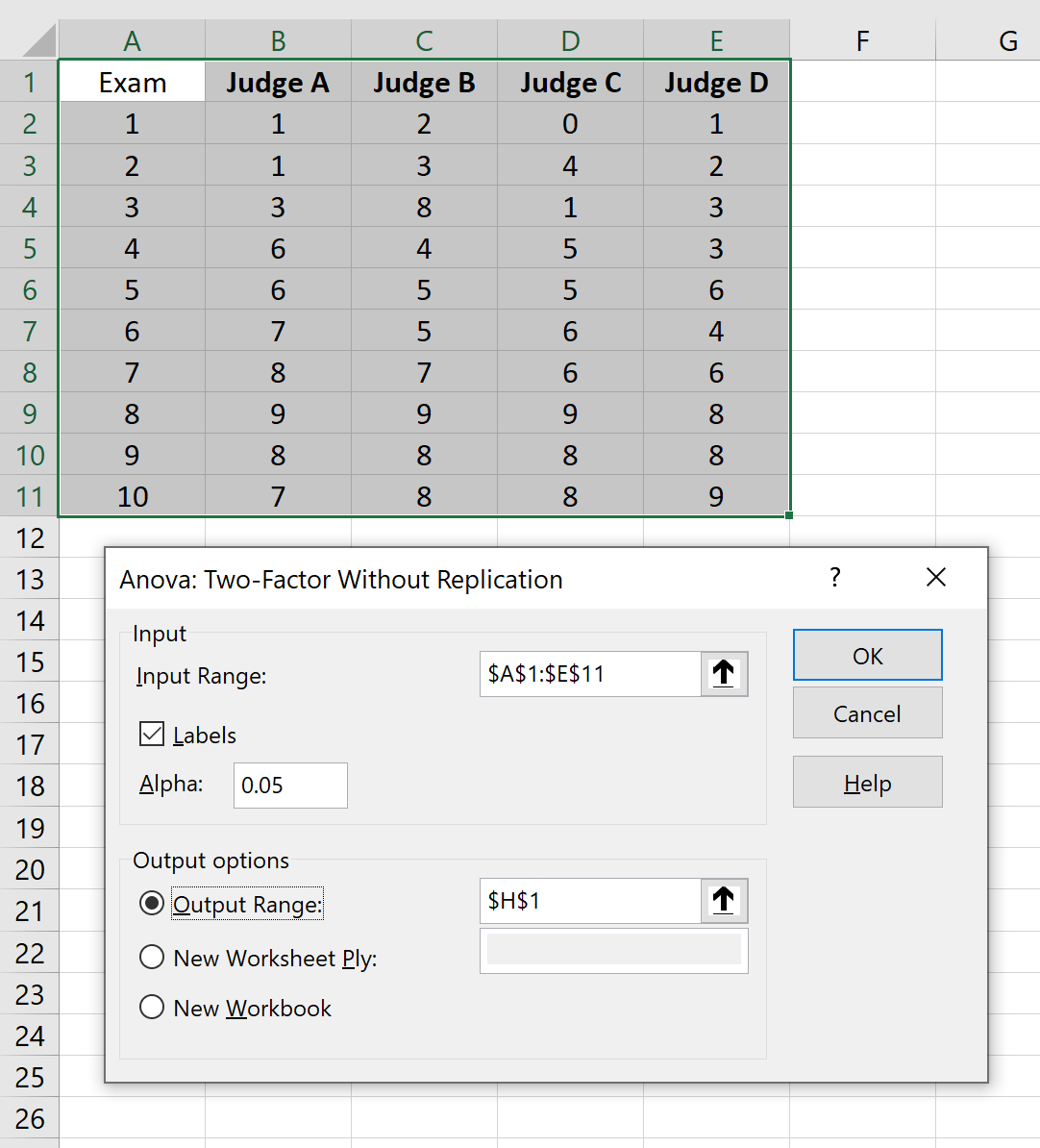
Pojawią się następujące wyniki:

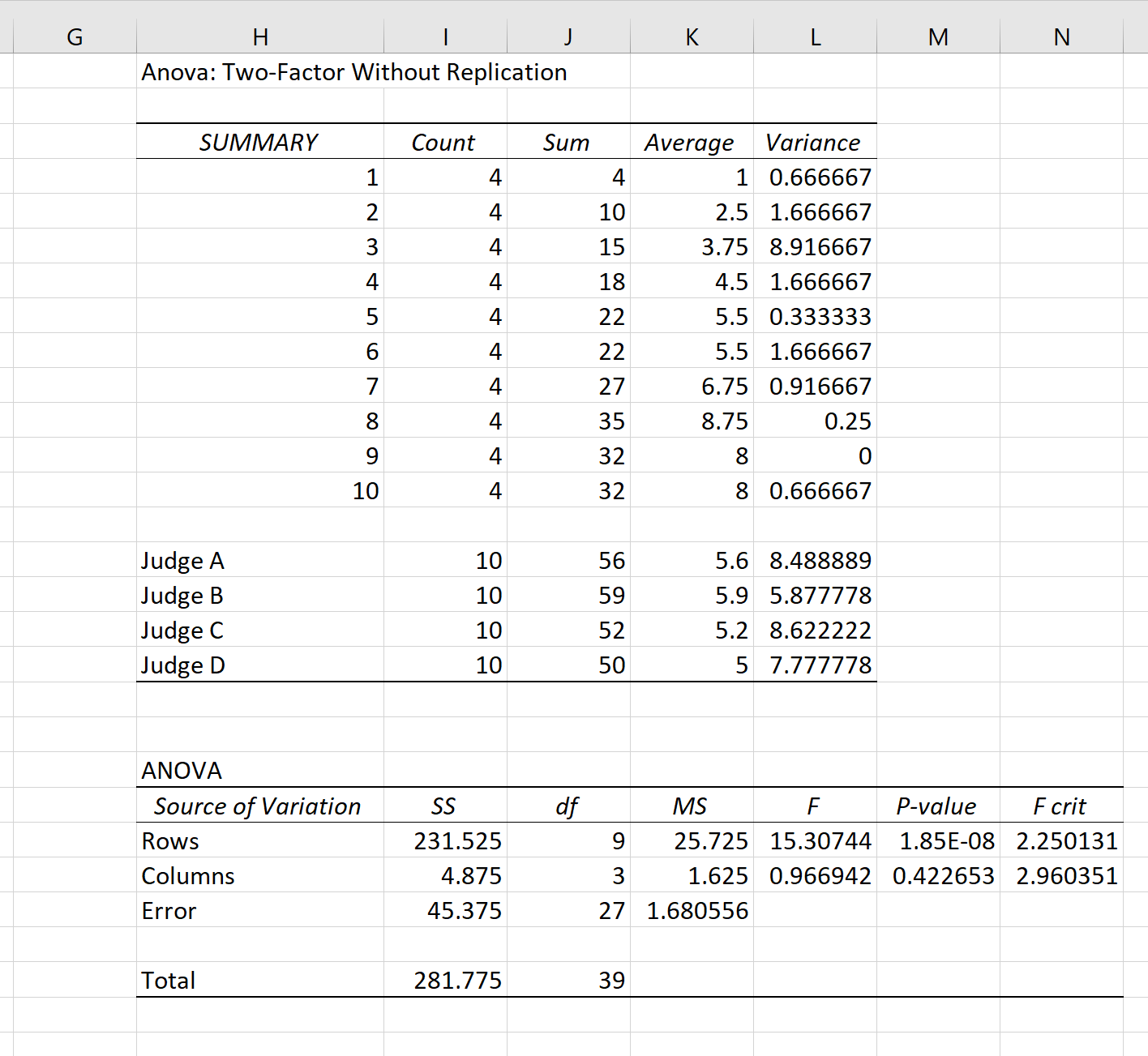
Krok 3: Oblicz współczynnik korelacji wewnątrzklasowej

Do obliczenia ICC wśród oceniających możemy użyć następującego wzoru:

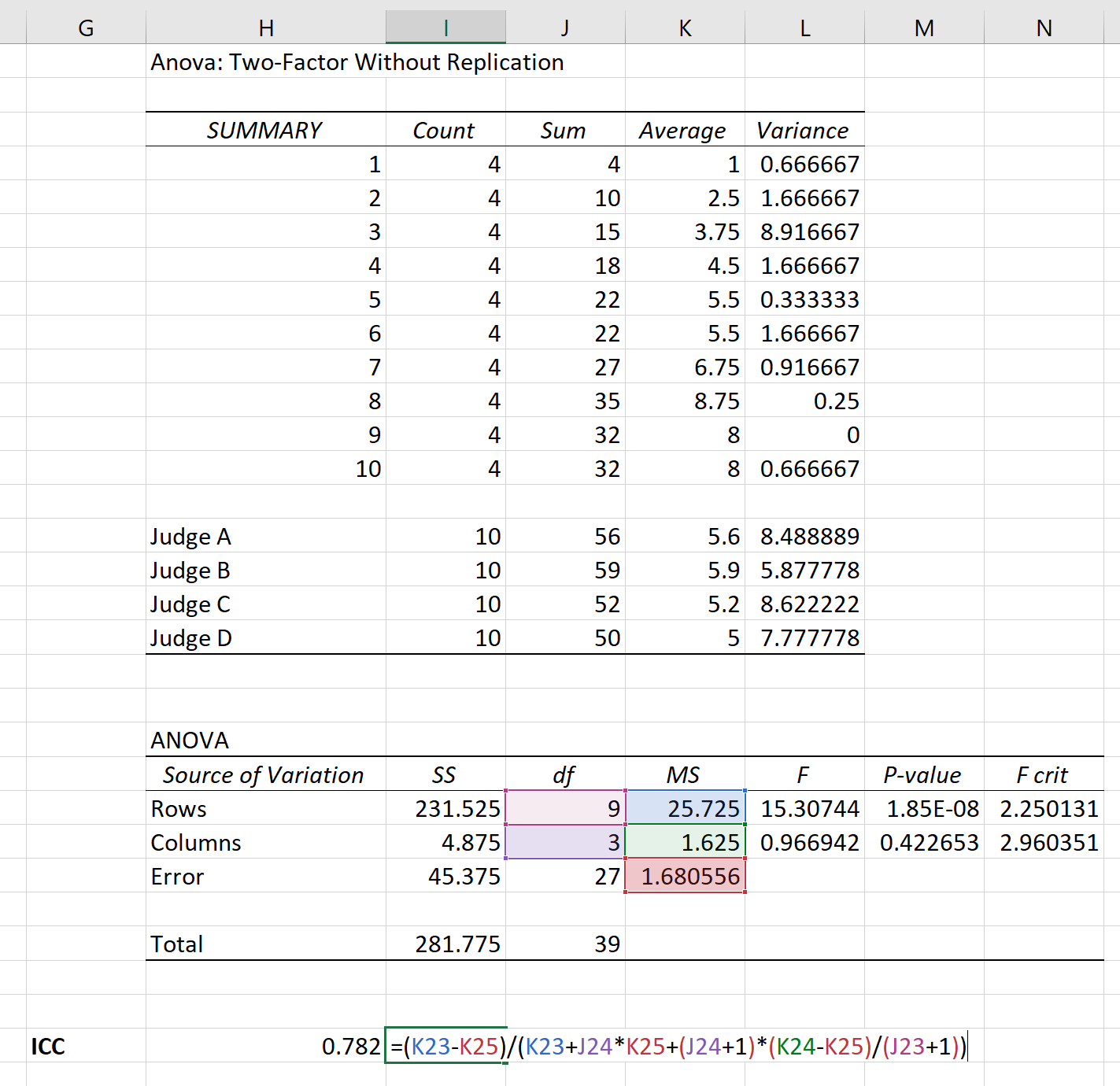
Stwierdzono, że współczynnik korelacji wewnątrzklasowej (ICC) wynosi 0,782 .

Według Koo i Li , oto jak interpretować wartość współczynnika korelacji wewnątrzklasowej:

• Mniej niż 0,50: słaba niezawodność
• Między 0,5 a 0,75: Umiarkowana niezawodność
• Między 0,75 a 0,9: Dobra niezawodność
• Większa niż 0,9: Doskonała niezawodność

Można zatem stwierdzić, że ICC wynoszący 0,782 wskazuje, że różni osoby oceniające mogą oceniać egzaminy z „dobrą” wiarygodnością.

Uwaga dotycząca obliczania ICC

Istnieje kilka różnych wersji ICC, które można obliczyć, w zależności od następujących trzech czynników:

• Model: jednokierunkowe efekty losowe, dwukierunkowe efekty losowe lub dwukierunkowe efekty mieszane
• Rodzaj relacji: konsekwencja lub absolutna zgoda
• Jednostka: pojedynczy oceniający lub średnia oceniających

W poprzednim przykładzie obliczony przez nas ICC przyjął następujące założenia:

• Model: dwukierunkowe efekty losowe
• Rodzaj relacji: Absolutna zgoda
• Jednostka: Pojedynczy asesor

Szczegółowe wyjaśnienie tych założeń znajdziesz w tym artykule .