4 przykłady braku korelacji pomiędzy zmiennymi

W statystyce korelacja jest miarą liniowej zależności między dwiema zmiennymi.

Wartość współczynnika korelacji zawsze mieści się w przedziale od -1 do 1, gdzie:

• -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
• Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
• 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi

Jeśli dwie zmienne mają korelację równą zero, oznacza to, że nie są ze sobą w żaden sposób powiązane. Innymi słowy, znajomość wartości jednej zmiennej nie daje nam pojęcia, jaka może być wartość drugiej zmiennej.

Jeśli utworzymy wykres rozrzutu dwóch zmiennych, które mają zerową korelację, na wykresie nie będzie wyraźnego wzoru:

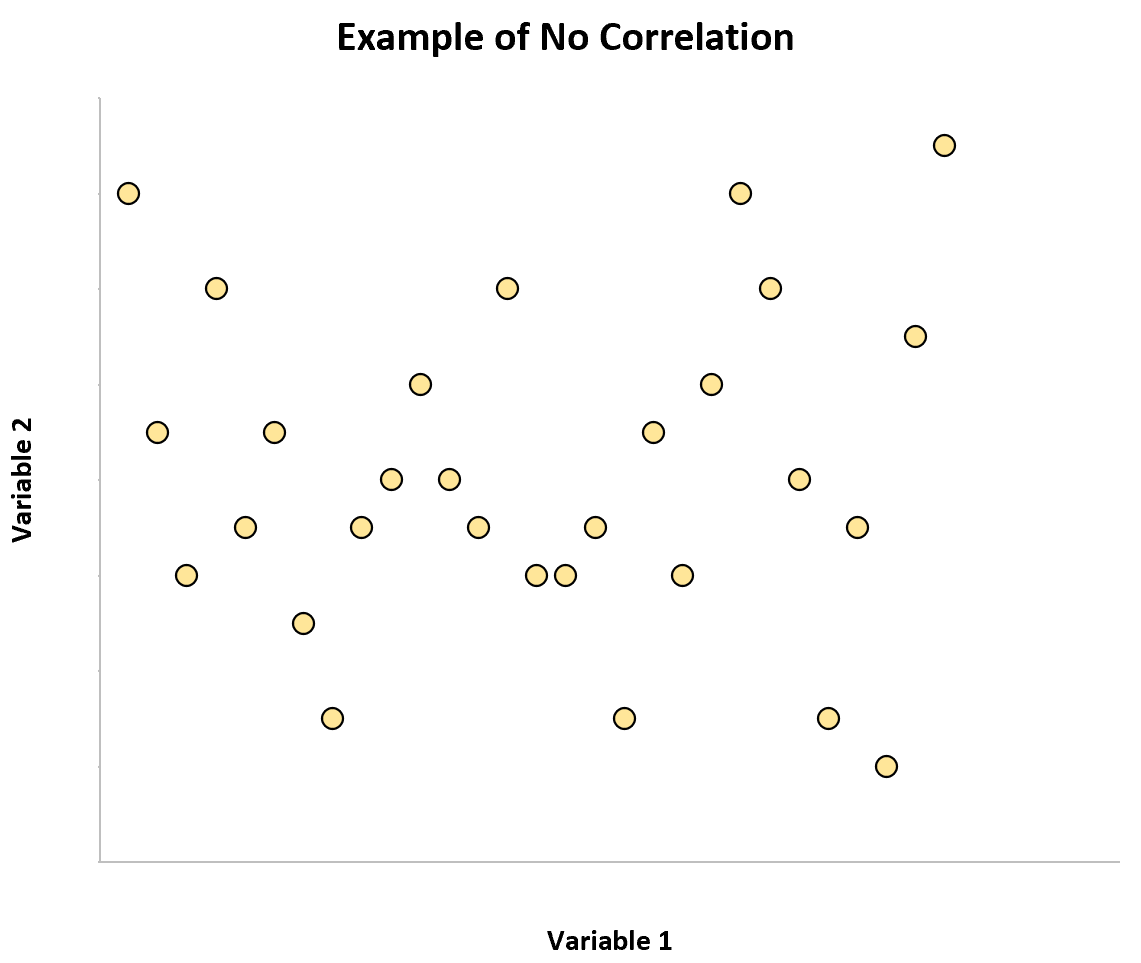
Przykłady braku korelacji

Poniższe przykłady ilustrują scenariusze, w których dwie zmienne nie mają korelacji.

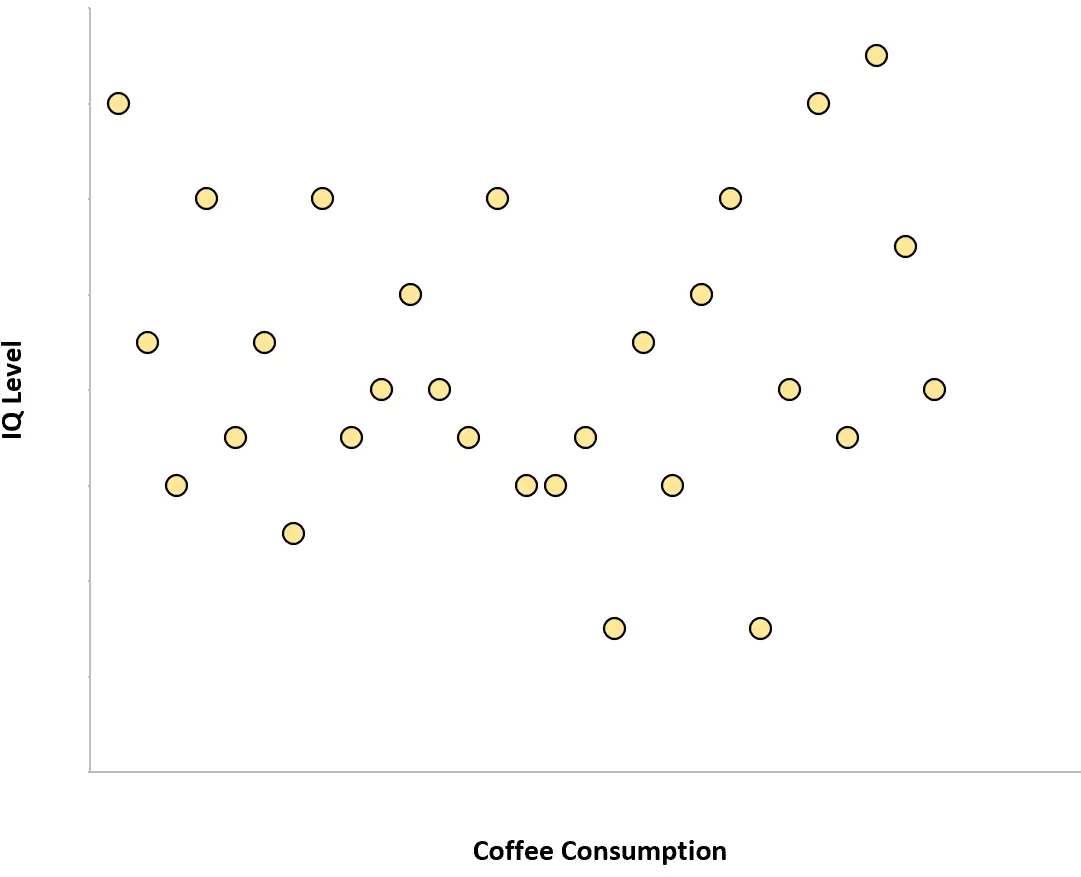
Przykład 1: Konsumpcja kawy a inteligencja

Ilość kawy spożywanej przez poszczególne osoby i ich poziom IQ mają zerową korelację. Innymi słowy, wiedza o tym, ile kawy wypija dana osoba, nie daje nam wyobrażenia o jej poziomie IQ.

Gdybyśmy stworzyli wykres rozrzutu dziennego spożycia kawy w zależności od poziomu IQ, wyglądałoby to następująco:

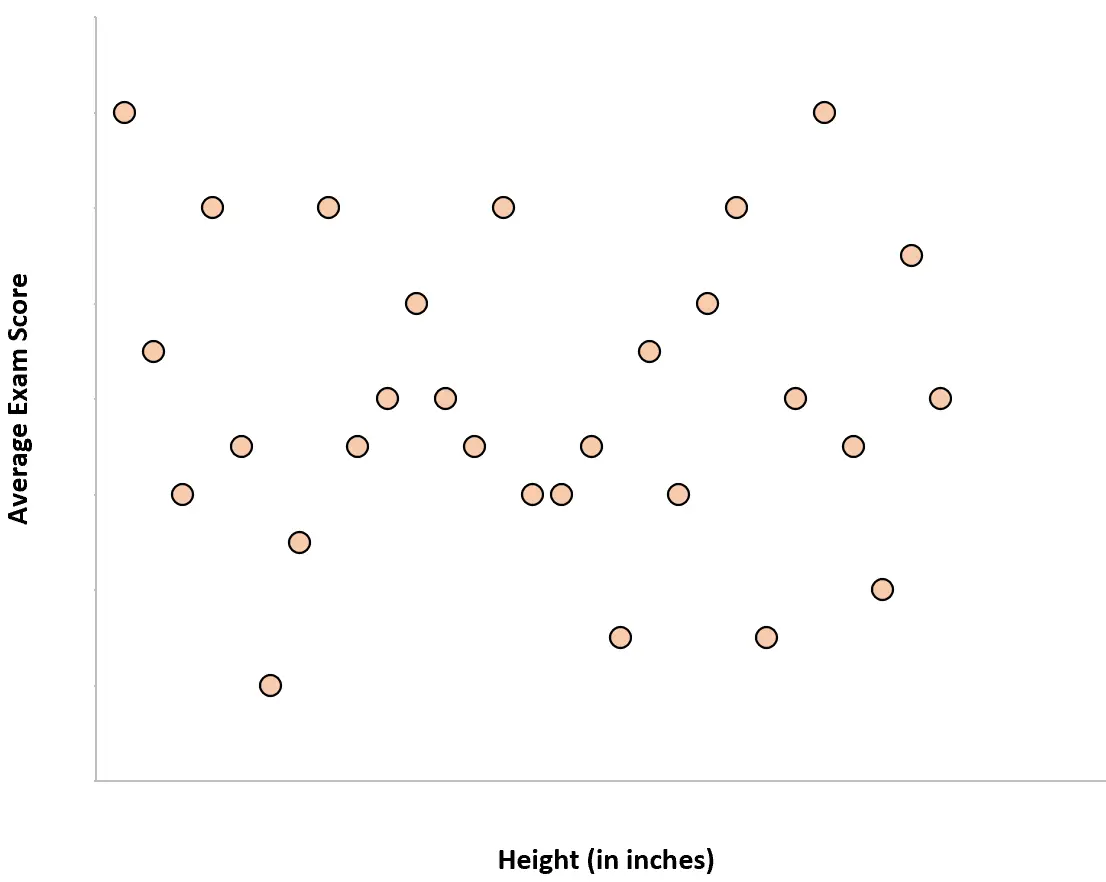
Przykład 2: Wzrost i wyniki testów

Wzrost uczniów i ich średnie wyniki w testach mają korelację zerową. Innymi słowy, znajomość wzrostu danej osoby nie daje nam wyobrażenia o jej średnim wyniku z egzaminu.

Gdybyśmy utworzyli wykres rozrzutu przedstawiający wzrost w funkcji średniego wyniku egzaminu, wyglądałby tak:

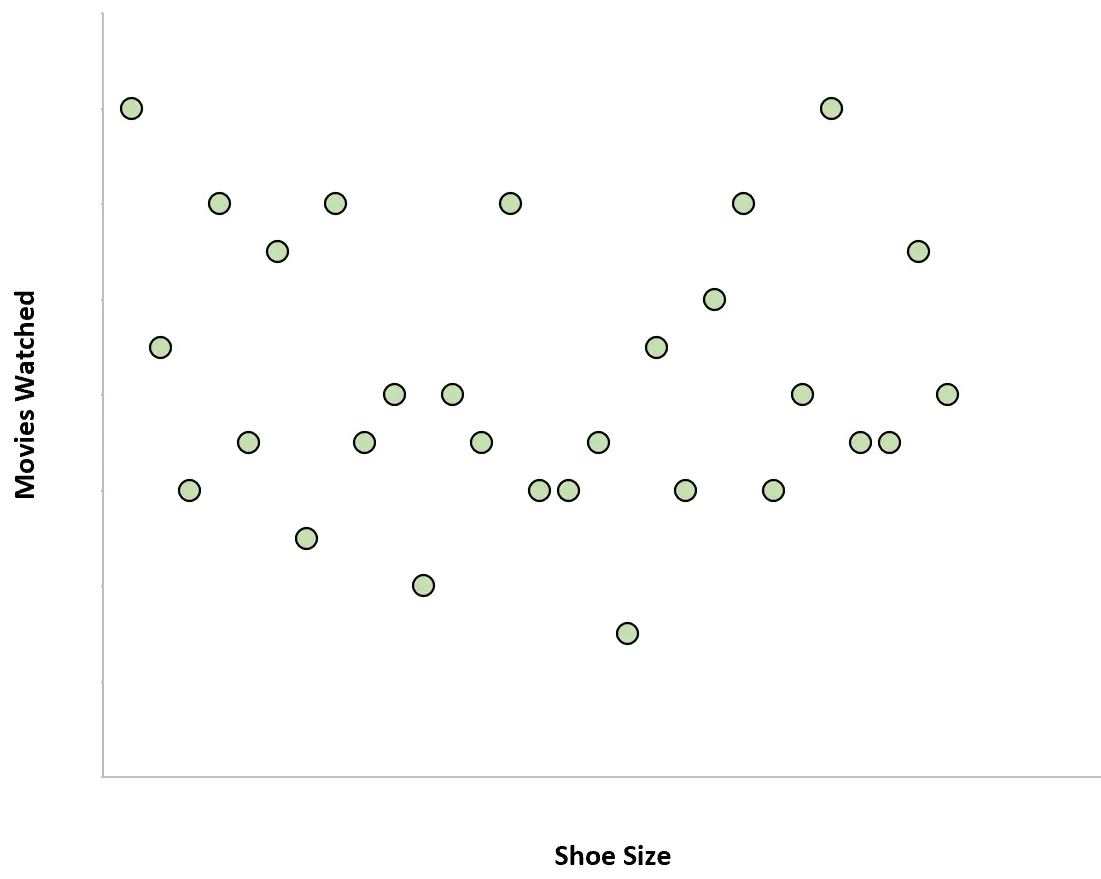
Przykład 3: rozmiar buta i oglądane filmy

Rozmiar buta danej osoby i liczba filmów, które oglądają w ciągu roku, mają zerową korelację. Innymi słowy, znajomość rozmiaru buta danej osoby nie daje nam pojęcia, ile filmów ogląda ona rocznie.

Gdybyśmy stworzyli wykres punktowy przedstawiający rozmiar buta w zależności od liczby obejrzanych filmów, wyglądałby tak:

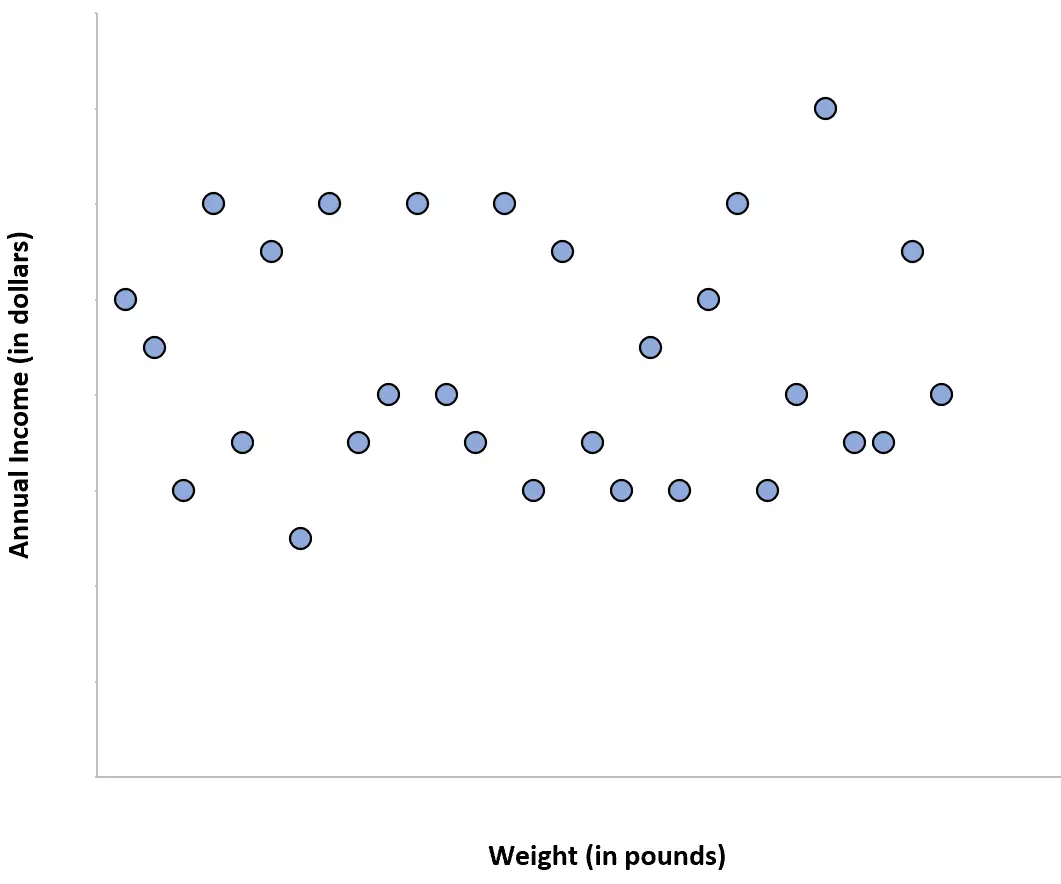
Przykład 4: waga i dochód

Masa osób i ich roczny dochód mają zerową korelację. Innymi słowy, znajomość wagi danej osoby nie daje nam wyobrażenia o tym, jaki może być jej roczny dochód.

Gdybyśmy utworzyli wykres rozrzutu wagi/dochodu, wyglądałby tak:

Dodatkowe zasoby

Wprowadzenie do współczynnika korelacji Pearsona
Korelacja vs. skojarzenie: jaka jest różnica?
Korelacja a regresja: jaka jest różnica?