Jak wykonać test scheffe w programie excel

Jednoczynnikową ANOVA stosuje się do określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub więcej niezależnych grup.

Jeśli ogólna wartość p tabeli ANOVA jest poniżej pewnego poziomu istotności, wówczas mamy wystarczające dowody, aby stwierdzić, że co najmniej jedna ze średnich grupowych różni się od pozostałych.

Nie mówi nam to jednak , które grupy różnią się od siebie. To po prostu mówi nam, że nie wszystkie średnie grupowe są równe.

Aby dokładnie wiedzieć, które grupy się od siebie różnią, musimy przeprowadzićtest post-hoc , który może kontrolować poziom błędów w przeliczeniu na rodzinę .

Jednym z najczęściej stosowanych testów post hoc jest test Scheffe’a.

Poniższy przykład pokazuje krok po kroku jak wykonać test Scheffe w programie Excel.

Krok 1: Wprowadź dane

Załóżmy, że nauczyciel chce wiedzieć, czy trzy różne techniki uczenia się prowadzą do różnych wyników uczniów w testach. Aby to sprawdzić, losowo przydziela 10 uczniów do stosowania każdej techniki uczenia się i rejestruje wyniki ich egzaminów.

Najpierw wpiszemy oceny każdego ucznia w oparciu o zastosowaną technikę uczenia się:

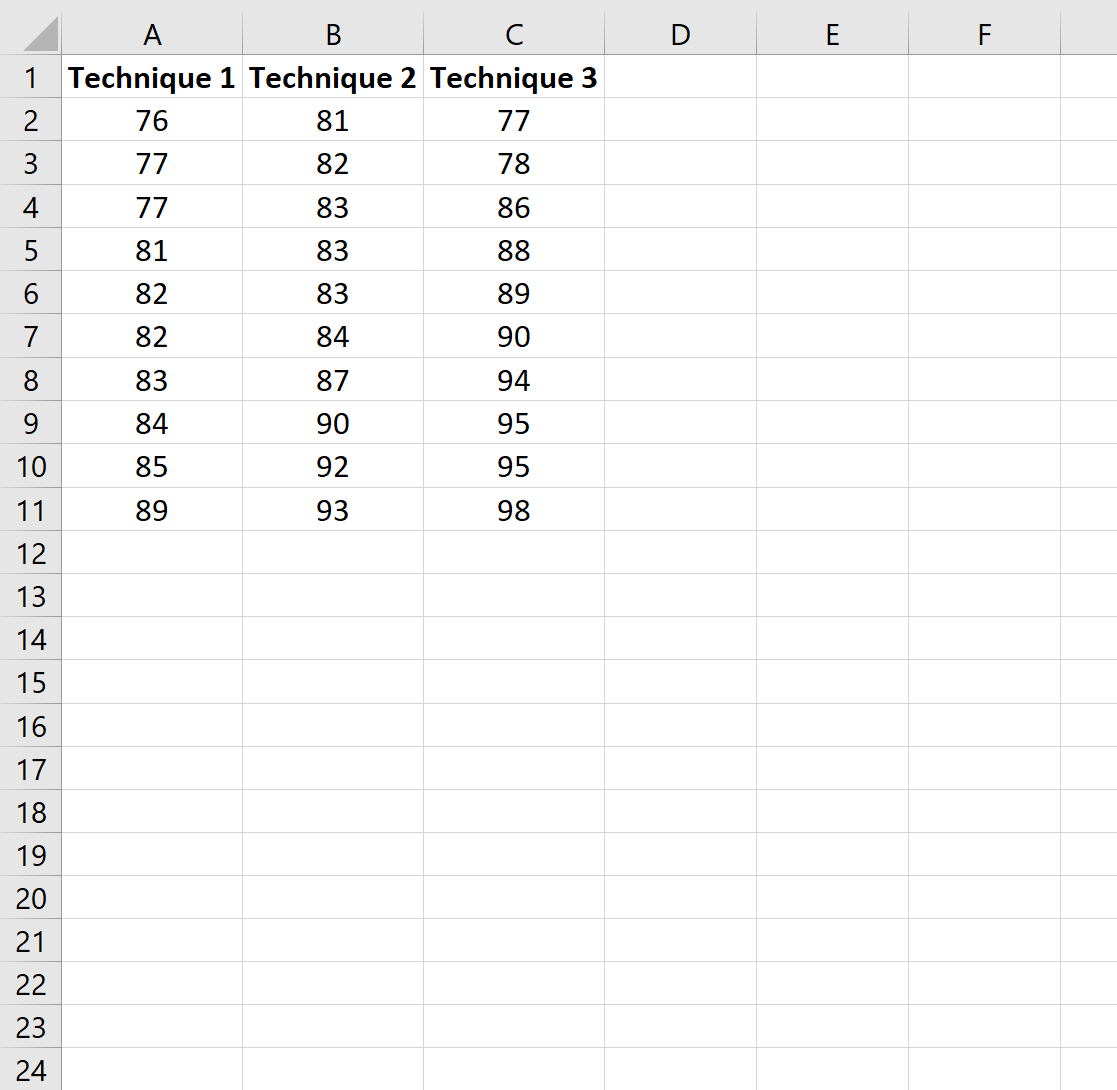
Krok 2: Wykonaj jednokierunkową ANOVA

Aby wykonać jednokierunkową analizę ANOVA, kliknij kartę Dane na górnej wstążce, a następnie kliknij opcję Analiza danych w grupie Analiza .

Jeśli nie widzisz tej opcji, musisz najpierw załadować pakiet Analysis ToolPak .

W nowym oknie, które się pojawi, kliknij Anova: Single Factor, a następnie kliknij OK .

W nowym oknie, które się pojawi, podaj następujące informacje:

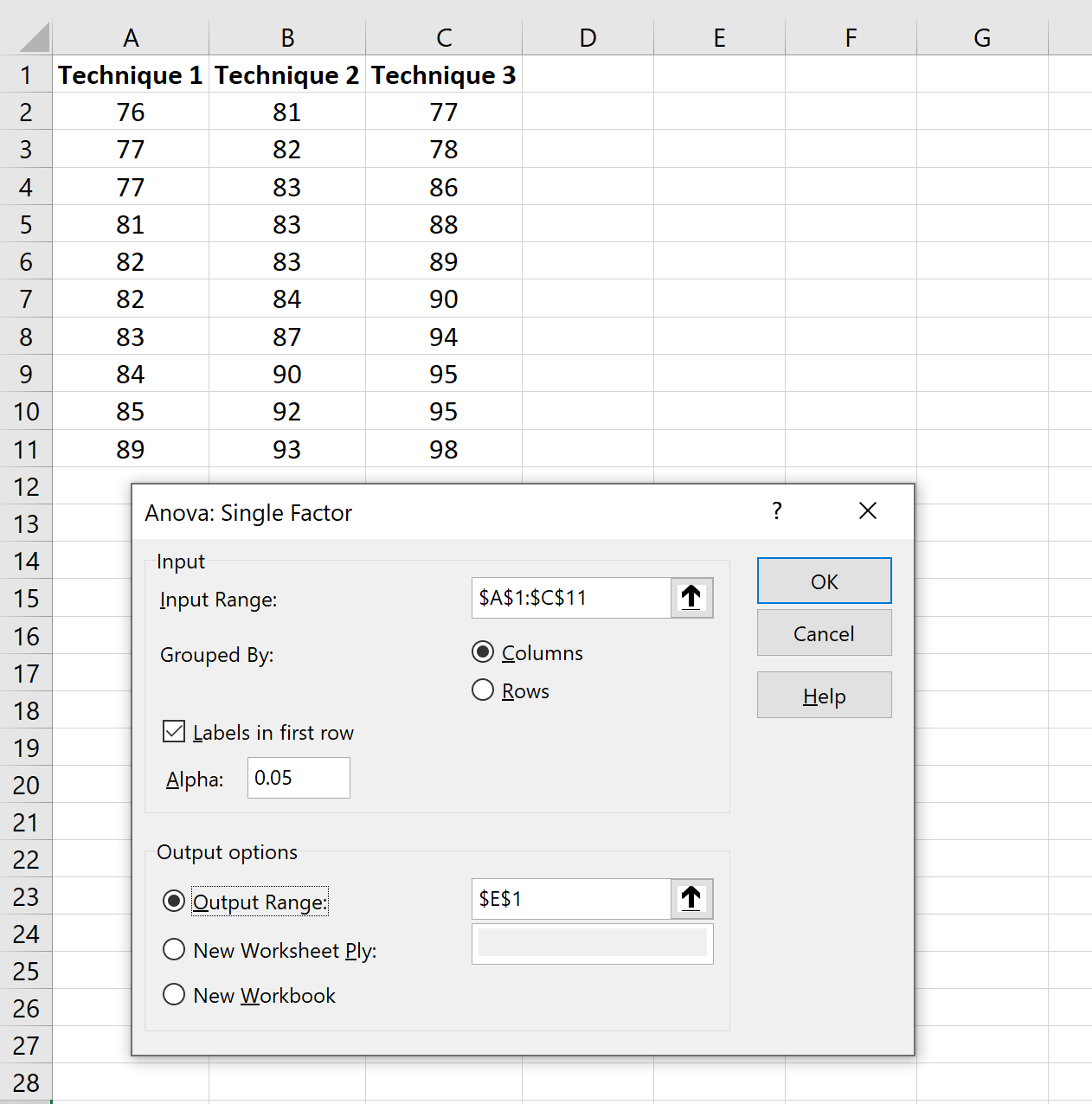
Po kliknięciu OK pojawią się jednokierunkowe wyniki ANOVA:

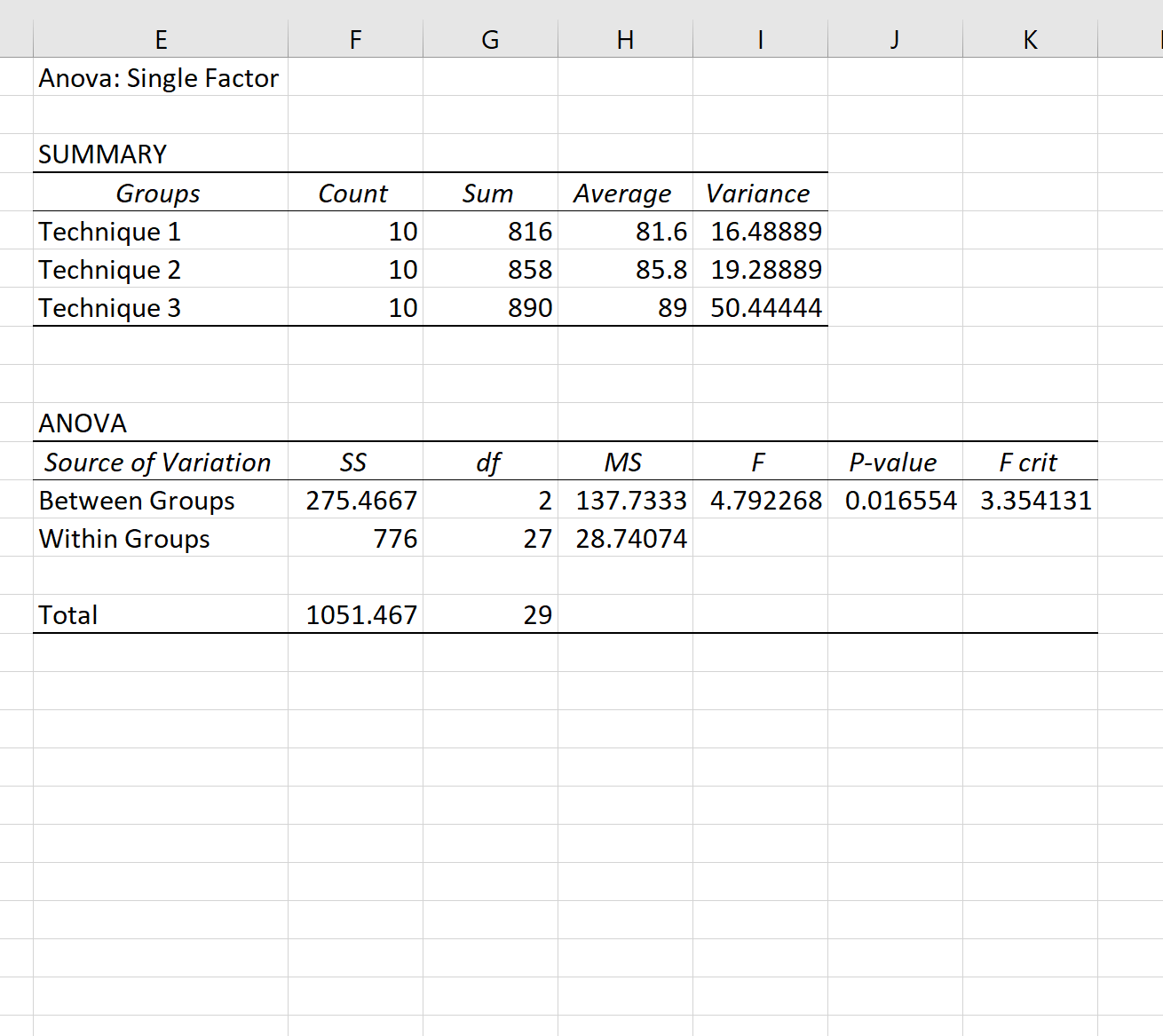
Ponieważ ogólna wartość p ( 0,016554 ) w tabeli ANOVA jest mniejsza niż 0,05, oznacza to, że każda grupa nie ma tego samego średniego wyniku egzaminu.

Następnie przeprowadzimy test Scheffe’a, aby określić, które grupy są różne.

Krok 3: Wykonaj test Scheffe’a

Najpierw musimy obliczyć wartość krytyczną Scheffe’a. Oblicza się to w następujący sposób:

Wartość krytyczna Scheffe’a = F Wartość krytyczna * 2

W naszym przykładzie wartość krytyczna Scheffe’a wynosi 3,354131 * 2 = 6,708 .

Następnie możemy obliczyć statystykę F dla każdego porównania parami, która jest obliczana w następujący sposób:

Statystyka F: ( x ₁ – x ₂ ) ² / (MS _in (1/n ₁ + 1/n ₂ ))

Na przykład możemy użyć następujących wzorów do obliczenia statystyki F dla różnicy parami pomiędzy każdą techniką:

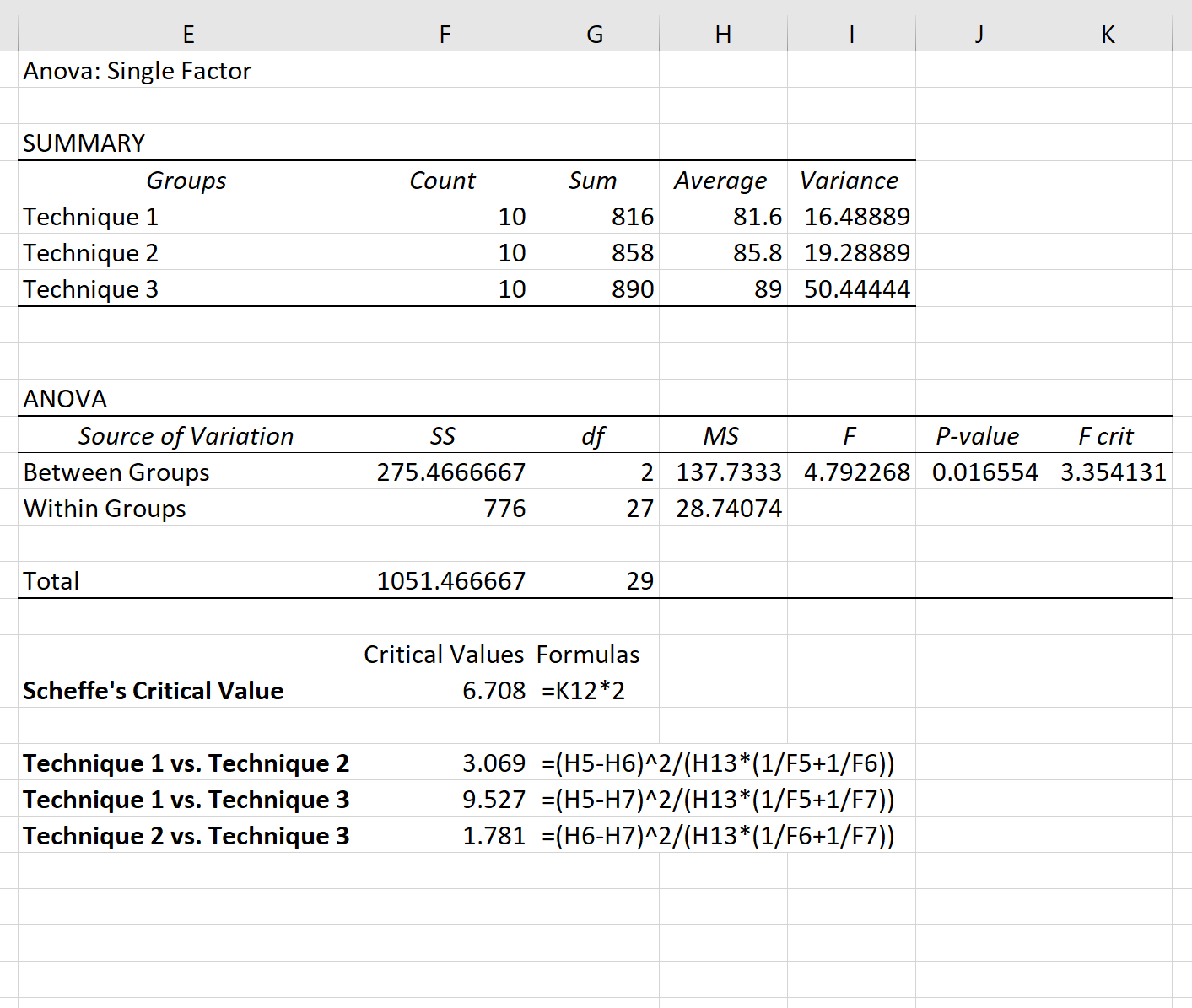
Jedyną statystyką F, która przekracza wartość krytyczną Scheffe’a, jest ta z porównania techniki 1 i techniki 3.

Zatem jedynymi dwiema statystycznie istotnie różnymi grupami są technika 1 i technika 3.

Dodatkowe zasoby

Jak wykonać jednokierunkową ANOVA w programie Excel
Jak wykonać dwukierunkową ANOVA w programie Excel
Jak wykonać test post hoc Tukeya-Kramera w programie Excel