Co jest uważane za „słabe”; korelacja?
W statystyce często staramy się zrozumieć, w jaki sposób dwie zmienne odnoszą się do siebie. Na przykład możemy chcieć wiedzieć:
- Jaka jest zależność pomiędzy liczbą godzin nauki studenta a oceną, jaką uzyska z egzaminu?
- Jaka jest zależność pomiędzy temperaturą zewnętrzną a liczbą batoników sprzedanych przez food trucka?
- Jaki jest związek pomiędzy dolarami wydanymi na reklamę a całkowitymi przychodami uzyskanymi przez daną firmę?
W każdym scenariuszu chcemy zrozumieć związek między dwiema zmiennymi.
Jednym z najczęstszych sposobów ilościowego określenia związku między dwiema zmiennymi jest użycie współczynnika korelacji Pearsona , który jest miarą liniowego związku między dwiema zmiennymi.
Zawsze przyjmuje wartość z zakresu od -1 do 1, gdzie:
- -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
- Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
- 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi
Często oznaczana r , liczba ta pomaga nam zrozumieć siłę związku między dwiema zmiennymi. Im r jest bliższe zeru, tym słabszy związek między dwiema zmiennymi .
Należy zauważyć, że dwie zmienne mogą mieć słabą dodatnią korelację lub słabą ujemną korelację.
Słaba dodatnia korelacja: gdy jedna zmienna rośnie, druga zmienna również ma tendencję do wzrostu, ale tylko słabo lub niewiarygodnie.
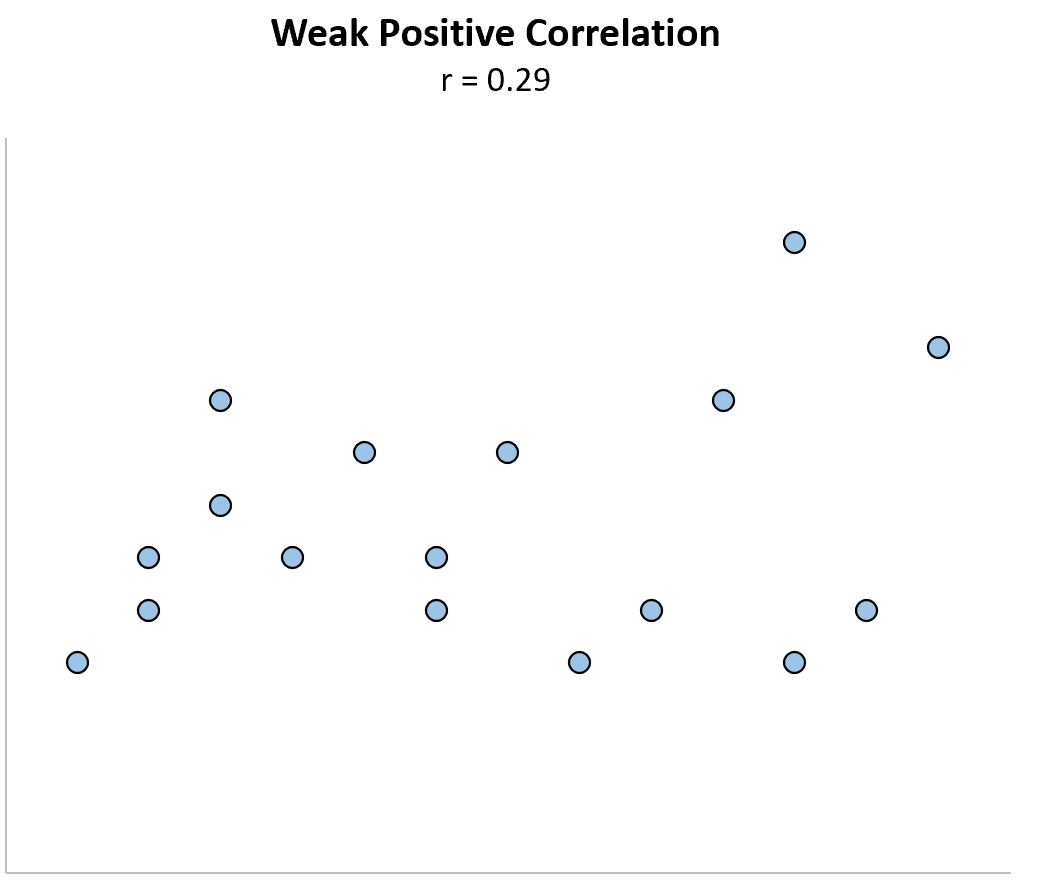
Niska ujemna korelacja: gdy jedna zmienna rośnie, druga zmienna ma tendencję do zmniejszania się, ale tylko słabo lub niewiarygodnie.
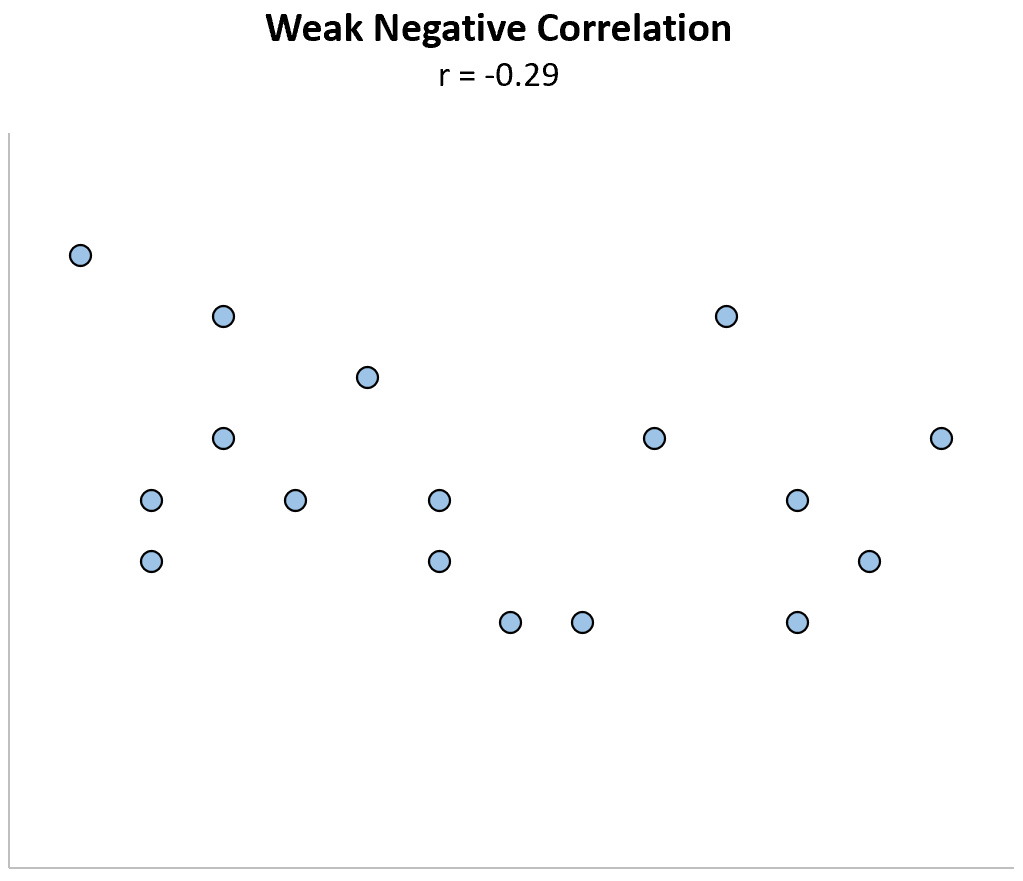
Poniższa tabela przedstawia praktyczną zasadę interpretacji siły związku między dwiema zmiennymi w oparciu o wartość r :
| Wartość bezwzględna r | Siła związku |
|---|---|
| r < 0,25 | Brak relacji |
| 0,25 < r < 0,5 | Słaby związek |
| 0,5 < r < 0,75 | Umiarkowane relacje |
| r > 0,75 | Silne relacje |
Korelację między dwiema zmiennymi uważa się za niską, jeśli wartość bezwzględna r mieści się w przedziale od 0,25 do 0,5.
Jednakże definicja „słabej” korelacji może się różnić w zależności od dziedziny.
Medyczny
W medycynie definicja „słabego” związku jest często znacznie niższa. Jeśli związek między przyjmowaniem danego leku a redukcją zawałów serca wynosi r = 0,2, w innych dziedzinach można to uznać za „brak związku”, ale w medycynie jest to na tyle istotne, że warto zażywać lek, aby zmniejszyć ryzyko zawału serca . mam atak serca.
Zasoby ludzkie
W dziedzinie takiej jak zasoby ludzkie częściej stosuje się niższe korelacje. Na przykład wykazano, że korelacja między średnią ocen na studiach a wynikami w pracy wynosi w przybliżeniu r = 0,16 . To dość niewiele, ale na tyle ważne, że firma powinna przynajmniej wziąć to pod uwagę podczas rozmowy kwalifikacyjnej.
Technologia
W dziedzinach technologii korelacja między zmiennymi może wymagać znacznie wyższej wartości, aby można ją było uznać za „niską”. Na przykład, jeśli firma tworzy samochód autonomiczny i korelacja między decyzjami o skręceniu samochodu a prawdopodobieństwem uniknięcia wypadku wynosi r = 0,95 , można to uznać za „słabą” korelację i prawdopodobnie jest ona zbyt słaba, aby samochód mógł należy uznać za bezpieczne, ponieważ zła decyzja może zakończyć się śmiercią.
Użyj wykresów rozrzutu, aby zwizualizować korelacje
Przy obliczaniu współczynnika korelacji między dwiema zmiennymi przydatne jest utworzenie wykresu rozrzutu w celu wizualizacji korelacji.
W szczególności chmury punktów mają dwie zalety:
1. Wykresy rozrzutu mogą pomóc w identyfikacji wartości odstających, które wpływają na współczynnik korelacji.
Skrajna wartość odstająca może mieć duży wpływ na współczynnik korelacji. Rozważmy poniższy przykład, w którym zmienne X i Y mają współczynnik korelacji Pearsona wynoszący r = 0,91 .
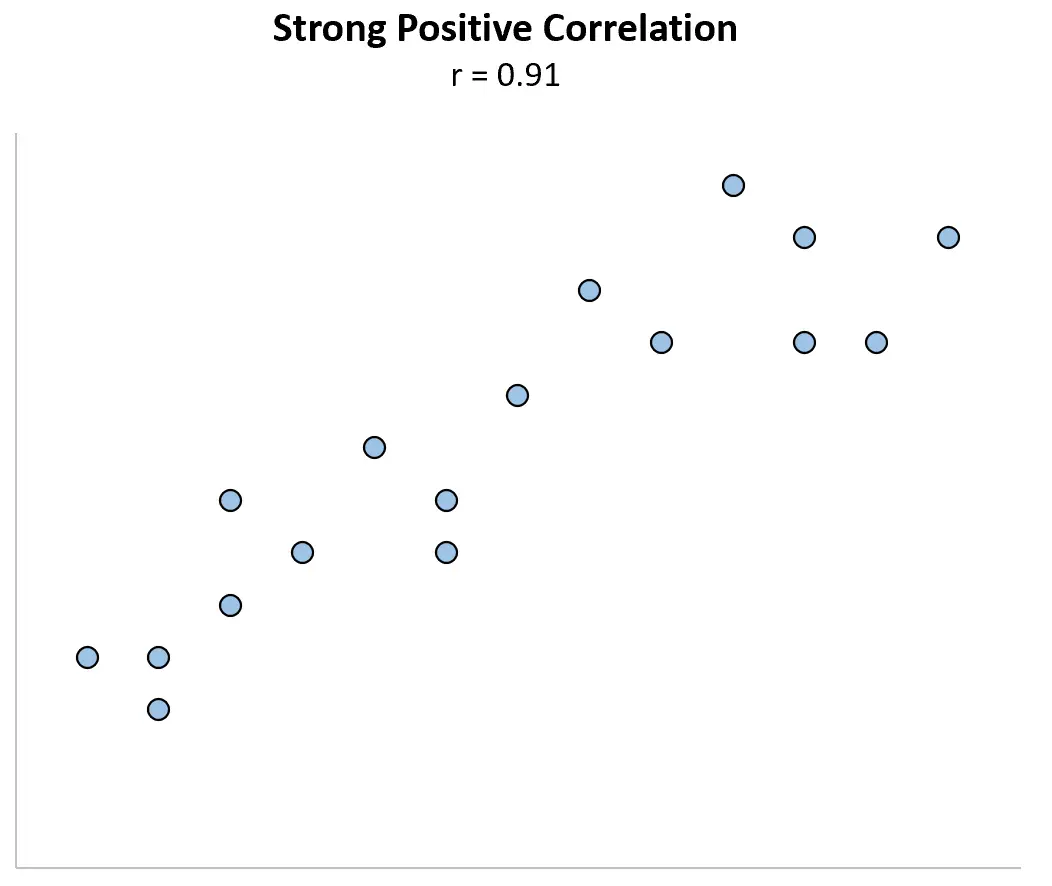
Teraz wyobraź sobie, że zmieniamy pierwszy punkt danych na znacznie większy. Współczynnik korelacji nagle staje się r = 0,29 .
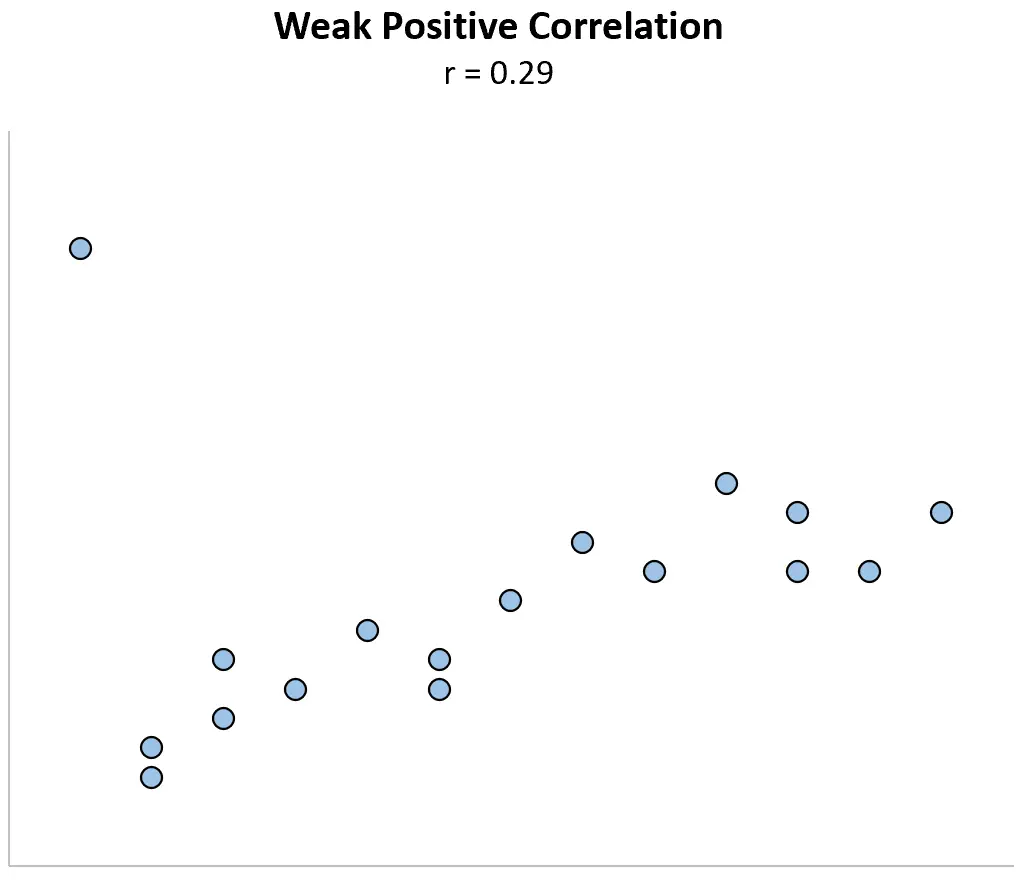
Ten pojedynczy punkt danych zmienia współczynnik korelacji z silnie dodatniej zależności na słabo dodatnią.
(2) Wykresy rozrzutu mogą pomóc w identyfikacji nieliniowych zależności między zmiennymi.
Współczynnik korelacji Pearsona po prostu mówi nam, czy dwie zmienne są powiązane liniowo . Ale nawet jeśli współczynnik korelacji Pearsona mówi nam, że dwie zmienne nie są skorelowane, nadal mogą istnieć między nimi pewien rodzaj nieliniowej zależności.
Rozważmy na przykład poniższy wykres rozrzutu pomiędzy zmiennymi X i Y , w którym ich korelacja wynosi r = 0,00 .
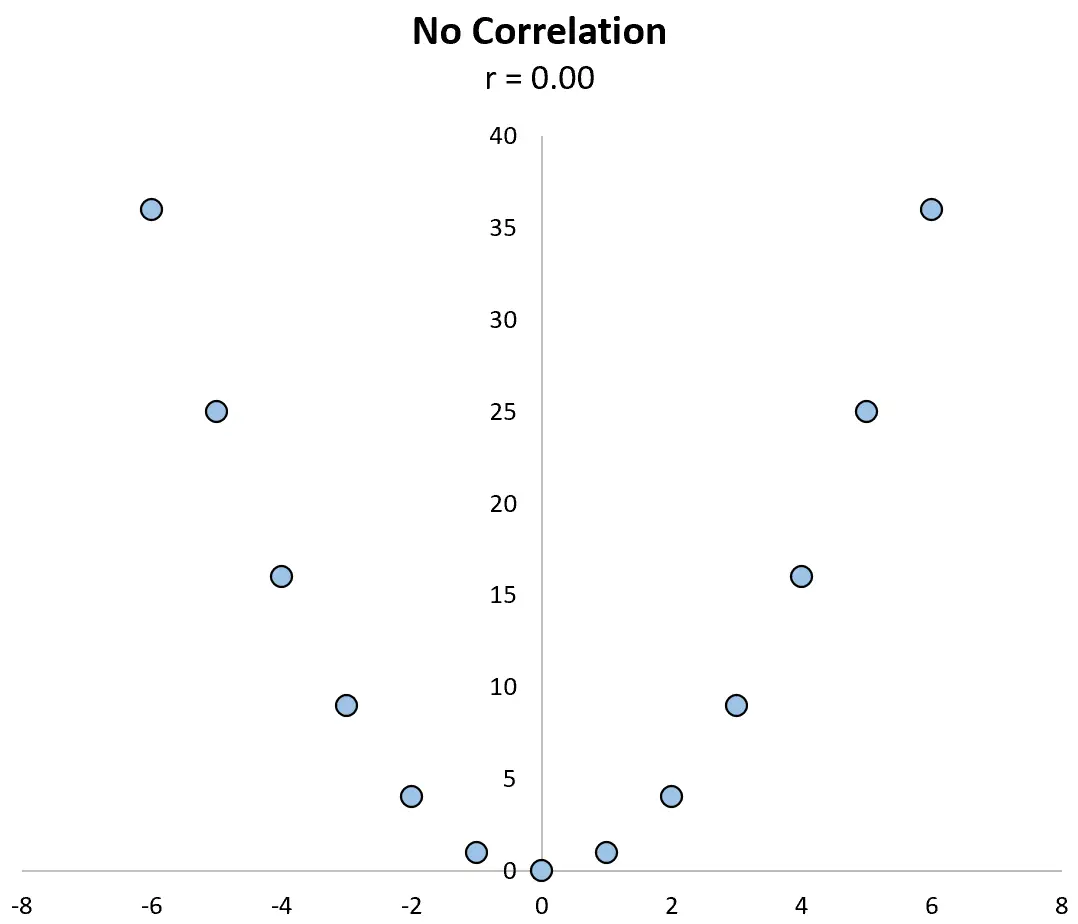
Zmienne wyraźnie nie mają związku liniowego, ale mają związek nieliniowy: wartości y to po prostu wartości x podniesione do kwadratu.
Sam współczynnik korelacji nie mógłby wykryć tej zależności, ale wykres rozrzutu mógłby to zrobić.
Wniosek
W podsumowaniu:
1. Ogólnie rzecz biorąc, współczynnik korelacji pomiędzy 0,25 a 0,5 jest uważany za „słabą” korelację pomiędzy dwiema zmiennymi.
2. Ta praktyczna zasada może się różnić w zależności od obszaru. Na przykład znacznie niższą korelację można uznać za słabą w dziedzinie medycyny w porównaniu z dziedziną technologii. Pamiętaj, aby skorzystać ze swojej wiedzy merytorycznej, aby zdecydować, co uważa się za niską korelację.
3. Używając współczynnika korelacji do opisania związku między dwiema zmiennymi, pomocne jest również utworzenie wykresu punktowego, aby można było zidentyfikować wartości odstające w zbiorze danych, a także potencjalną zależność nieliniową.
Dodatkowe zasoby
Co uważa się za „silną” korelację?
Kalkulator macierzy korelacji
Korelacja vs. skojarzenie: jaka jest różnica?