Jak ręcznie utworzyć ścieżkę resztkową

Wykres reszt to rodzaj wykresu, który wyświetla wartości zmiennej predykcyjnej w modelu regresji wzdłuż osi x i wartości reszt wzdłuż osi y.

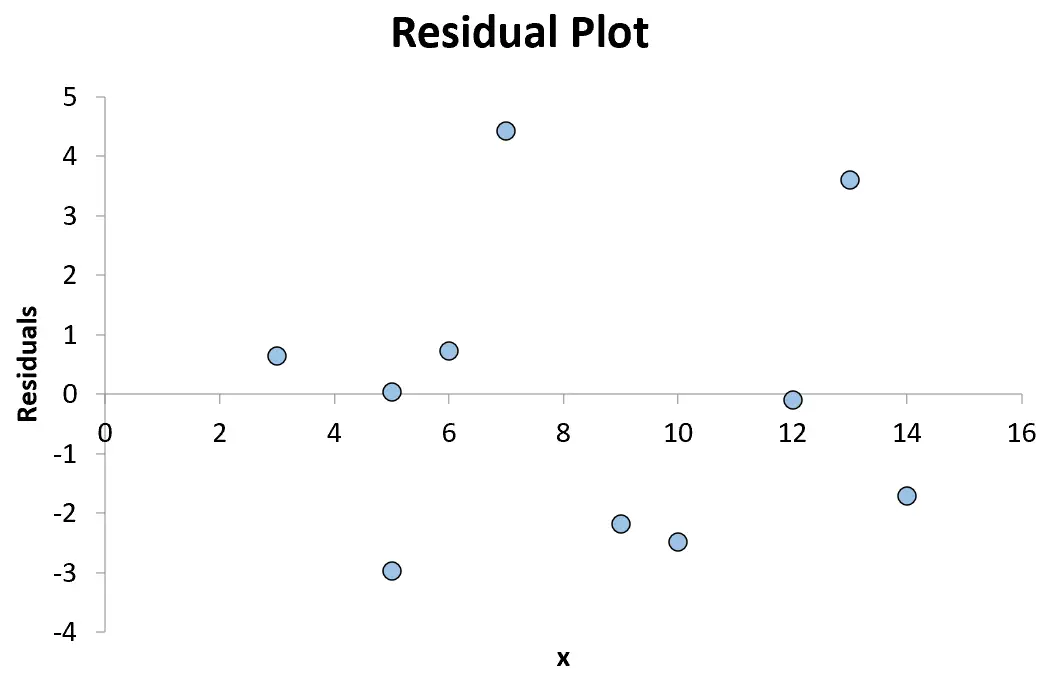
Wykres ten służy do oceny, czy reszty modelu regresji mają rozkład normalny i czy wykazują heteroskedastyczność .

Poniższy przykład pokazuje krok po kroku, jak ręcznie utworzyć wykres reszt dla modelu regresji.

Krok 1: Znajdź przewidywane wartości

Załóżmy, że chcemy dopasować model regresji do następującego zbioru danych:

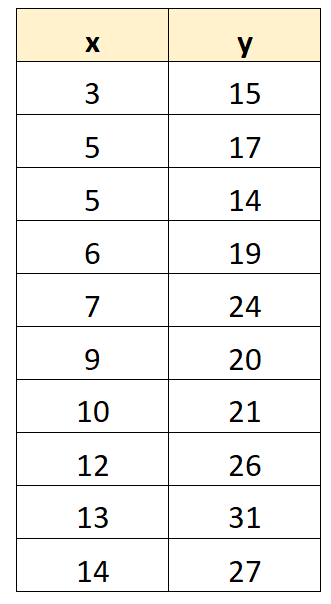
Korzystając z oprogramowania statystycznego (takiego jak Excel, R, Python, SPSS itp.), możemy zobaczyć, że dopasowany model regresji to:

y = 10,4486 + 1,3037(x)

Możemy następnie użyć tego modelu do przewidzenia wartości y na podstawie wartości x. Na przykład, jeśli x = 3, to przewidujemy, że y będzie:

y = 10,4486 + 1,3037(3) = 14,359

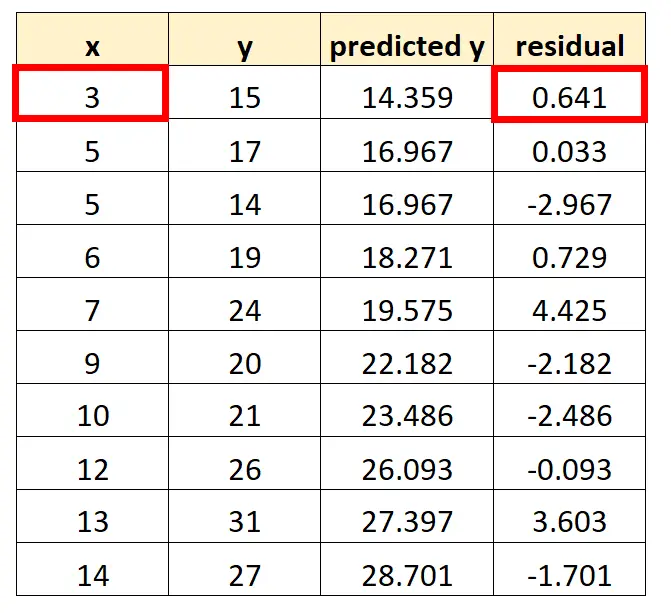
Możemy powtórzyć ten proces dla każdej obserwacji w naszym zbiorze danych:

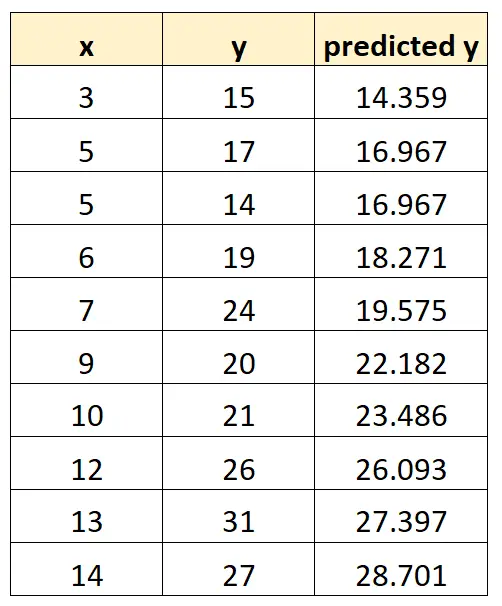
Krok 2: Znajdź pozostałości

Resztę dla danej obserwacji w naszym zbiorze danych oblicza się w następujący sposób:

Pozostałość = wartość obserwowana – wartość przewidywana

Na przykład resztę z pierwszej obserwacji można obliczyć w następujący sposób:

Reszta = 15 – 14,359 = 0,641

Możemy powtórzyć ten proces dla każdej obserwacji w naszym zbiorze danych:

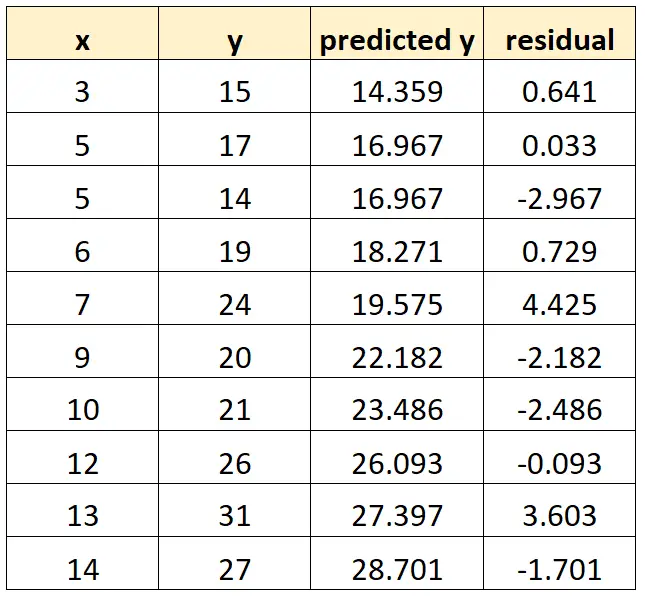
Krok 3: Utwórz wykres rezydualny

Na koniec możemy utworzyć wykres reszt, umieszczając wartości x wzdłuż osi x, a reszty wzdłuż osi y.

Na przykład pierwszy punkt, który umieścimy na naszym wykresie to (3, 0,641)

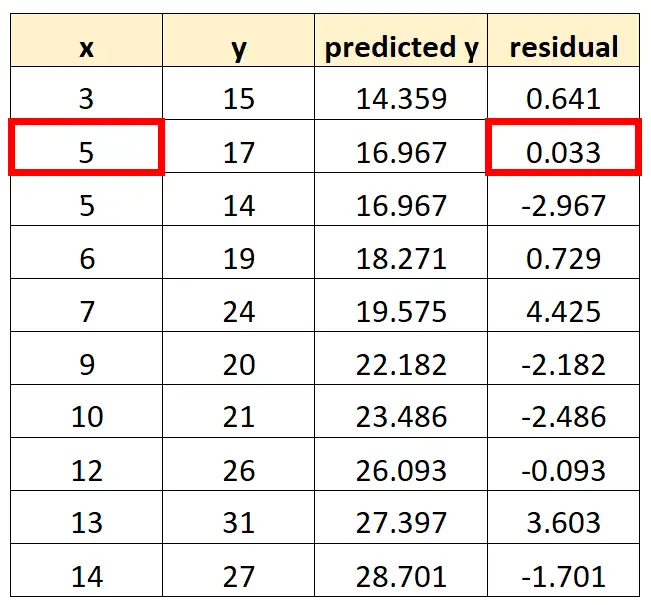
Następny punkt, który umieścimy na naszym wykresie to (5, 0,033)

Będziemy kontynuować, dopóki nie umieścimy na wykresie wszystkich 10 par kombinacji wartości x i reszt:

Każdy punkt powyżej zera na wykresie oznacza dodatnią resztę. Oznacza to, że zaobserwowana wartość y jest większa niż wartość przewidywana przez model regresji.

Każdy punkt mniejszy od zera oznacza resztę ujemną. Oznacza to, że zaobserwowana wartość y jest niższa od wartości przewidywanej przez model regresji.

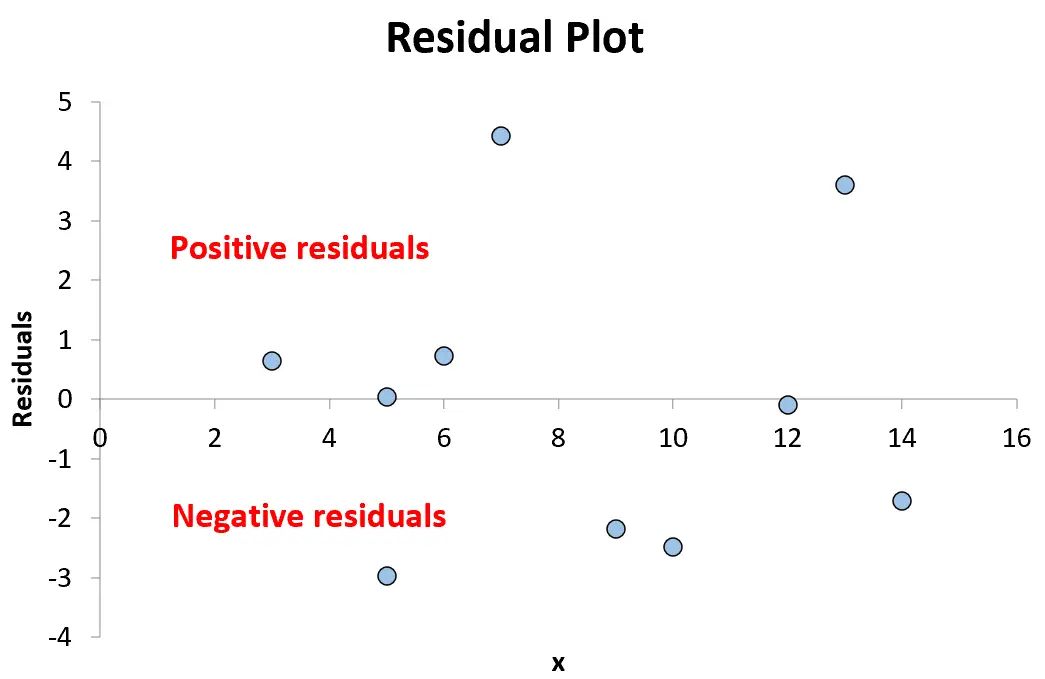
Ponieważ punkty na wykresie są losowo rozproszone wokół reszty równej 0 bez wyraźnego wzoru, oznacza to, że zależność między x i y jest liniowa i właściwe jest zastosowanie modelu regresji liniowej.

A ponieważ reszty nie rosną ani nie maleją systematycznie wraz ze wzrostem zmiennej predykcyjnej, oznacza to, że heteroskedastyczność nie stanowi problemu w tym modelu regresji.

Dodatkowe zasoby

Poniższe samouczki wyjaśniają, jak tworzyć wykresy reszt przy użyciu różnych programów statystycznych:

Jak utworzyć wykres pozostałości na kalkulatorze TI-84
Jak utworzyć wykres resztowy w programie Excel
Jak utworzyć wykres rezydualny w R
Jak utworzyć wykres resztkowy w Pythonie