R vs r-square: jaka jest różnica?
Dwa terminy, które uczniowie często mylą w statystyce, to R i R-kwadrat , często zapisywane jako R2 .
W kontekście prostej regresji liniowej :
- Odp.: Korelacja pomiędzy zmienną predykcyjną x i zmienną odpowiedzi y.
- R 2 : Proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennej predykcyjnej w modelu regresji.
Oraz w kontekście wielokrotnej regresji liniowej :
- Odp.: Korelacja między zaobserwowanymi wartościami zmiennej odpowiedzi a przewidywanymi wartościami zmiennej odpowiedzi określonymi przez model.
- R 2 : Proporcja wariancji zmiennej odpowiedzi, którą można wyjaśnić za pomocą zmiennych predykcyjnych modelu regresji.
Należy zauważyć, że wartość R2 mieści się w przedziale od 0 do 1. Im wartość jest bliższa 1, tym silniejszy związek pomiędzy zmiennymi predykcyjnymi a zmienną odpowiedzi.
Poniższe przykłady pokazują, jak interpretować wartości R i R-kwadrat w modelach prostej regresji liniowej i wielokrotnej regresji liniowej.
Przykład 1: Prosta regresja liniowa
Załóżmy, że mamy następujący zbiór danych, który pokazuje liczbę przepracowanych godzin i wyniki egzaminów uzyskane przez 12 uczniów na określonym kursie z matematyki:
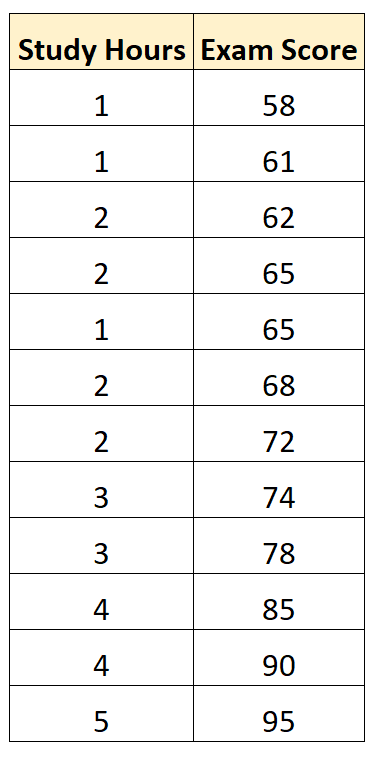
Korzystając z oprogramowania statystycznego (takiego jak Excel, R, Python, SPSS itp.), możemy dopasować prosty model regresji liniowej, wykorzystując „godziny nauki” jako zmienną predykcyjną i „ocenę z egzaminu” jakozmienną odpowiedzi .
Dla tego modelu możemy znaleźć następujące dane wyjściowe:
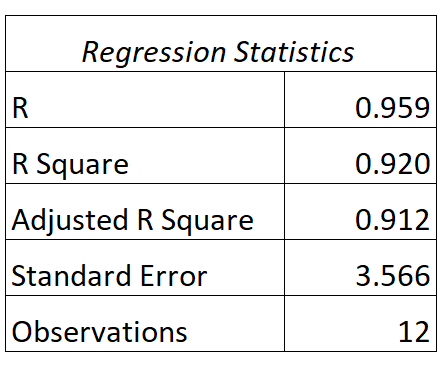
Oto jak interpretować wartości R i R kwadrat tego modelu:
- Odp.: Korelacja między przestudiowanymi godzinami a wynikiem egzaminu wynosi 0,959 .
- R2 : R kwadrat dla tego modelu regresji wynosi 0,920 . To mówi nam, że 92,0% różnic w wynikach egzaminów można wyjaśnić liczbą godzin nauki.
Należy również zauważyć, że wartość R 2 jest po prostu równa wartości R podniesionej do kwadratu:
R2 = R * R = 0,959 * 0,959 = 0,920
Przykład 2: Wielokrotna regresja liniowa
Załóżmy, że mamy następujący zbiór danych, który pokazuje liczbę przepracowanych godzin, aktualne oceny uczniów i oceny z egzaminów uzyskane przez 12 uczniów z określonego kursu matematyki:
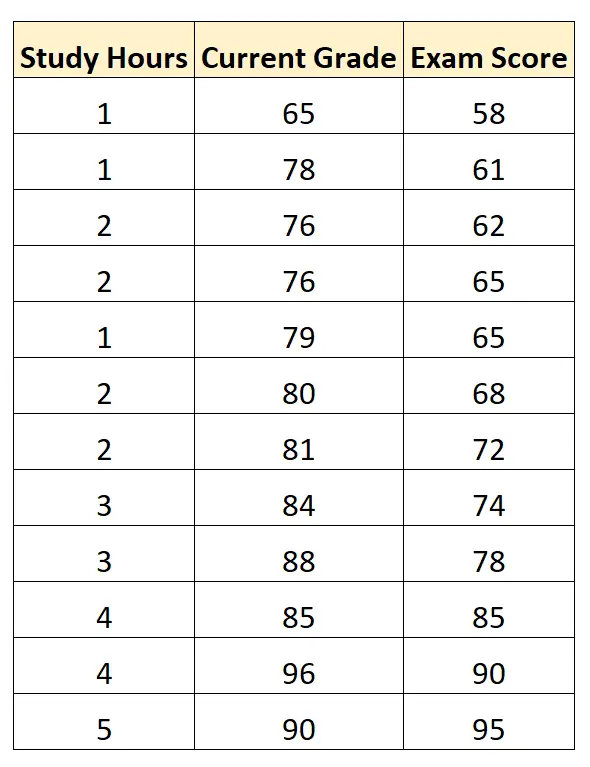
Korzystając z oprogramowania statystycznego, możemy dopasować model regresji liniowej, wykorzystując „godziny nauki” i „bieżącą ocenę” jako zmienne predykcyjne oraz „ocenę z egzaminu” jako zmienną odpowiedzi.
Dla tego modelu możemy znaleźć następujące dane wyjściowe:
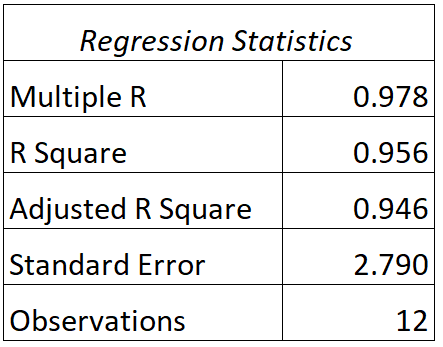
Oto jak interpretować wartości R i R kwadrat tego modelu:
- Odpowiedź: Korelacja między rzeczywistymi wynikami testów a wynikami testów przewidywanymi przez model wynosi 0,978 .
- R2 : R kwadrat dla tego modelu regresji wynosi 0,956 . To mówi nam, że 95,6% różnic w wynikach egzaminów można wyjaśnić liczbą przepracowanych godzin i aktualną oceną ucznia z zajęć.
Należy również zauważyć, że wartość R 2 jest po prostu równa wartości R podniesionej do kwadratu:
R2 = R * R = 0,978 * 0,978 = 0,956
Dodatkowe zasoby
Jaka jest dobra wartość R-kwadrat?
Delikatny przewodnik po sumie kwadratów: SST, SSR, SSE