Jak znaleźć prawdopodobieństwo, mając średnią i odchylenie standardowe

Możemy zastosować następujący proces, aby znaleźć prawdopodobieństwo, że zmienna losowa o rozkładzie normalnym

Krok 1: Znajdź wynik Z.

Wynik Z informuje, o ile odchyleń standardowych poszczególne wartości danych spadają od średniej. Oblicza się go w następujący sposób:

wynik z = (x – μ) / σ

Złoto:

• x: indywidualna wartość danych
• μ: średnia populacji
• σ: odchylenie standardowe populacji

Krok 2: Znajdź prawdopodobieństwo odpowiadające wynikowi z.

Po obliczeniu wyniku z możemy znaleźć odpowiadające mu prawdopodobieństwo w tabeli z.

Poniższe przykłady pokazują, jak używać tego procesu w różnych scenariuszach.

Przykład 1: Prawdopodobieństwo mniejsze niż pewna wartość

Wyniki pewnego testu mają rozkład normalny ze średnią μ = 82 i odchyleniem standardowym σ = 8. Jakie jest prawdopodobieństwo, że dany uczeń uzyska w teście mniej niż 84 punkty?

Krok 1: Znajdź wynik Z.

Najpierw znajdziemy wynik Z powiązany z wynikiem 84:

wynik z = (x – μ) / σ = (84 – 82) / 8 = 2/8 = 0,25

Krok 2: Użyj tabeli z, aby znaleźć odpowiednie prawdopodobieństwo.

Następnie będziemy szukać wartości 0,25 w tabeli z:

Prawdopodobieństwo, że dany uczeń uzyska mniej niż 84 punkty, wynosi około 59,87% .

Przykład 2: Prawdopodobieństwo większe niż pewna wartość

Wzrost niektórych gatunków pingwinów ma rozkład normalny ze średnią μ = 30 cali i odchyleniem standardowym σ = 4 cale. Jeśli wybierzemy losowo pingwina, jakie jest prawdopodobieństwo, że będzie on miał więcej niż 28 cali wzrostu?

Krok 1: Znajdź wynik Z.

Najpierw znajdziemy wskaźnik Z powiązany ze wzrostem 28 cali.

Wynik z = (x – μ) / σ = (28 – 30) / 4 = -2 / 4 = -0,5

Krok 2: Użyj tabeli z, aby znaleźć odpowiednie prawdopodobieństwo.

Następnie będziemy szukać wartości -0,5   w tabeli z:

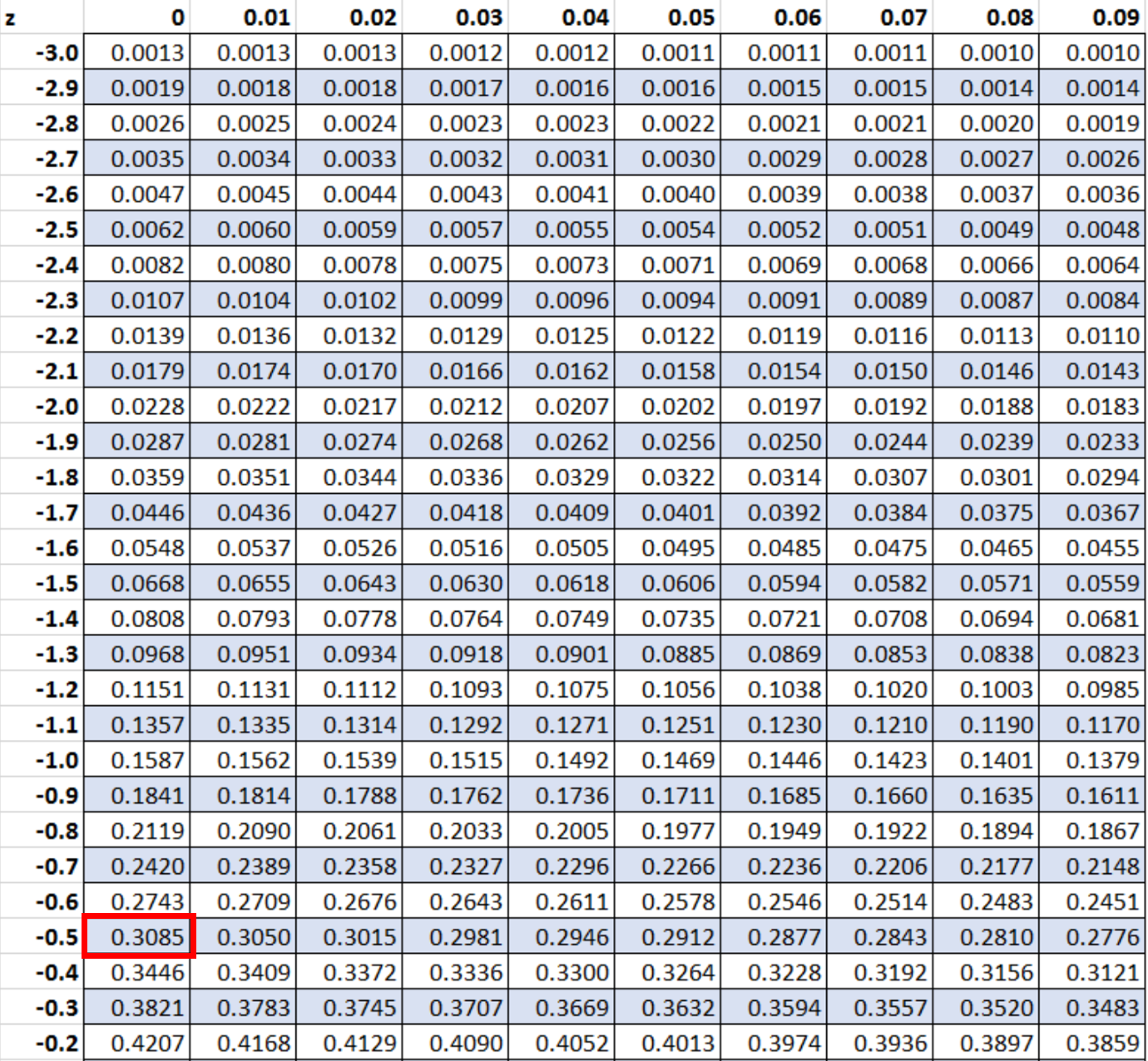
Wartość odpowiadająca wskaźnikowi Z wynoszącemu -0,5 wynosi 0,3085. Oznacza to prawdopodobieństwo, że pingwin będzie krótszy niż 28 cali.

Ponieważ jednak chcemy poznać prawdopodobieństwo, że pingwin jest wyższy niż 28 cali, musimy odjąć to prawdopodobieństwo od 1.

Zatem prawdopodobieństwo, że pingwin jest wyższy niż 28 cali, wynosi: 1 – 0,3085 = 0,6915 .

Przykład 3: Prawdopodobieństwo między dwiema wartościami

Masa określonego gatunku żółwia ma rozkład normalny ze średnią μ = 400 funtów i odchyleniem standardowym σ = 25 funtów. Jeśli wybierzemy losowo żółwia, jakie jest prawdopodobieństwo, że waży on od 410 do 425 funtów?

Krok 1: Znajdź wyniki Z.

Najpierw znajdziemy wartości Z powiązane z 410 książkami i 425 książkami

wynik z wynoszący 410 = (x – μ) / σ = (410 – 400) / 25 = 10/25 = 0,4

z wynik 425 = (x – μ) / σ = (425 – 400) / 25 = 25 / 25 = 1

Krok 2: Użyj tabeli z, aby znaleźć odpowiednie prawdopodobieństwo.

Najpierw będziemy szukać wartości 0,4   w tabeli z:

Następnie będziemy szukać wartości 1   w tabeli z:

Następnie odejmiemy mniejszą wartość od większej: 0,8413 – 0,6554 = 0,1859 .

Zatem prawdopodobieństwo, że losowo wybrany żółw waży od 410 do 425 funtów, wynosi 18,59% .

Dodatkowe zasoby

Jak ręcznie obliczyć wartość P na podstawie wyniku Z
Jak przekonwertować wyniki Z na wyniki surowe
Jak znaleźć wyniki Z w danym obszarze