Kompletny przewodnik: projekt czynnikowy 2×2

Projekt czynnikowy 2 × 2 to rodzaj projektu eksperymentalnego, który pozwala badaczom zrozumieć wpływ dwóch zmiennych niezależnych (każda z dwoma poziomami ) na pojedynczą zmienną zależną.

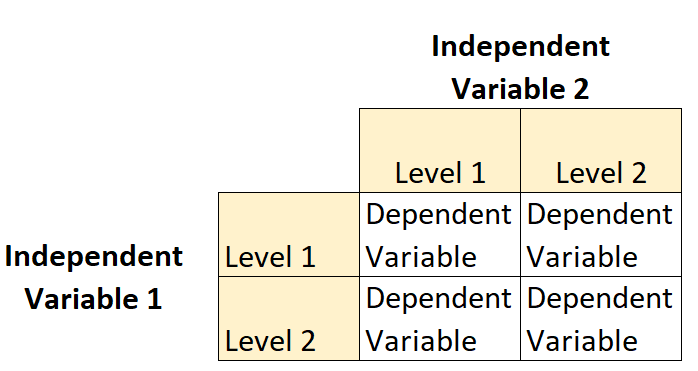
Załóżmy na przykład, że botanik chce zrozumieć wpływ światła słonecznego (niskiego lub wysokiego) i częstotliwości podlewania (codziennie lub co tydzień) na wzrost określonego gatunku roślin.

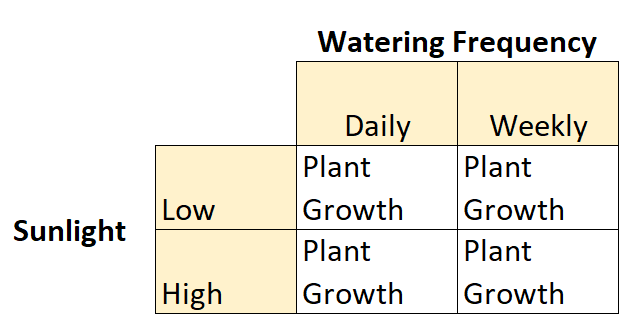
To jest przykład planu czynnikowego 2×2, ponieważ istnieją dwie niezależne zmienne, każda z dwoma poziomami:

• Zmienna niezależna nr 1: Światło słoneczne
  • Poziomy: niski, wysoki
• Zmienna niezależna nr 2: Częstotliwość podlewania
  • Poziomy: dzienny, tygodniowy

Istnieje również zmienna zależna: wzrost roślin.

Cel planu czynnikowego 2 × 2

Plan czynnikowy 2×2 umożliwia analizę następujących efektów:

Efekty główne: Są to skutki, jakie pojedyncza zmienna niezależna wywiera na zmienną zależną.

Na przykład w naszym poprzednim scenariuszu mogliśmy przeanalizować następujące efekty główne:

• Główny wpływ światła słonecznego na wzrost roślin.
  • Możemy znaleźć średni wzrost wszystkich roślin, które otrzymały niskie nasłonecznienie.
  • Możemy znaleźć średni wzrost wszystkich roślin, które otrzymały duże nasłonecznienie.
• Główny wpływ częstotliwości podlewania na wzrost roślin.
  • Możemy znaleźć średni wzrost wszystkich roślin podlewanych codziennie.
  • Możemy znaleźć średni wzrost wszystkich roślin podlewanych w każdym tygodniu.

Efekty interakcji: Występują, gdy wpływ jednej zmiennej niezależnej na zmienną zależną zależy od poziomu drugiej zmiennej niezależnej.

Na przykład w naszym poprzednim scenariuszu mogliśmy przeanalizować następujące efekty interakcji:

• Czy wpływ nasłonecznienia na wzrost roślin zależy od częstotliwości podlewania?
• Czy wpływ częstotliwości podlewania na wzrost roślin zależy od nasłonecznienia?

Wizualizuj efekty główne i efekty interakcji

Kiedy używamy planu czynnikowego 2 × 2, często sporządzamy wykresy średnich, aby lepiej zrozumieć wpływ, jaki zmienne niezależne wywierają na zmienną zależną.

Rozważmy na przykład następujący wykres:

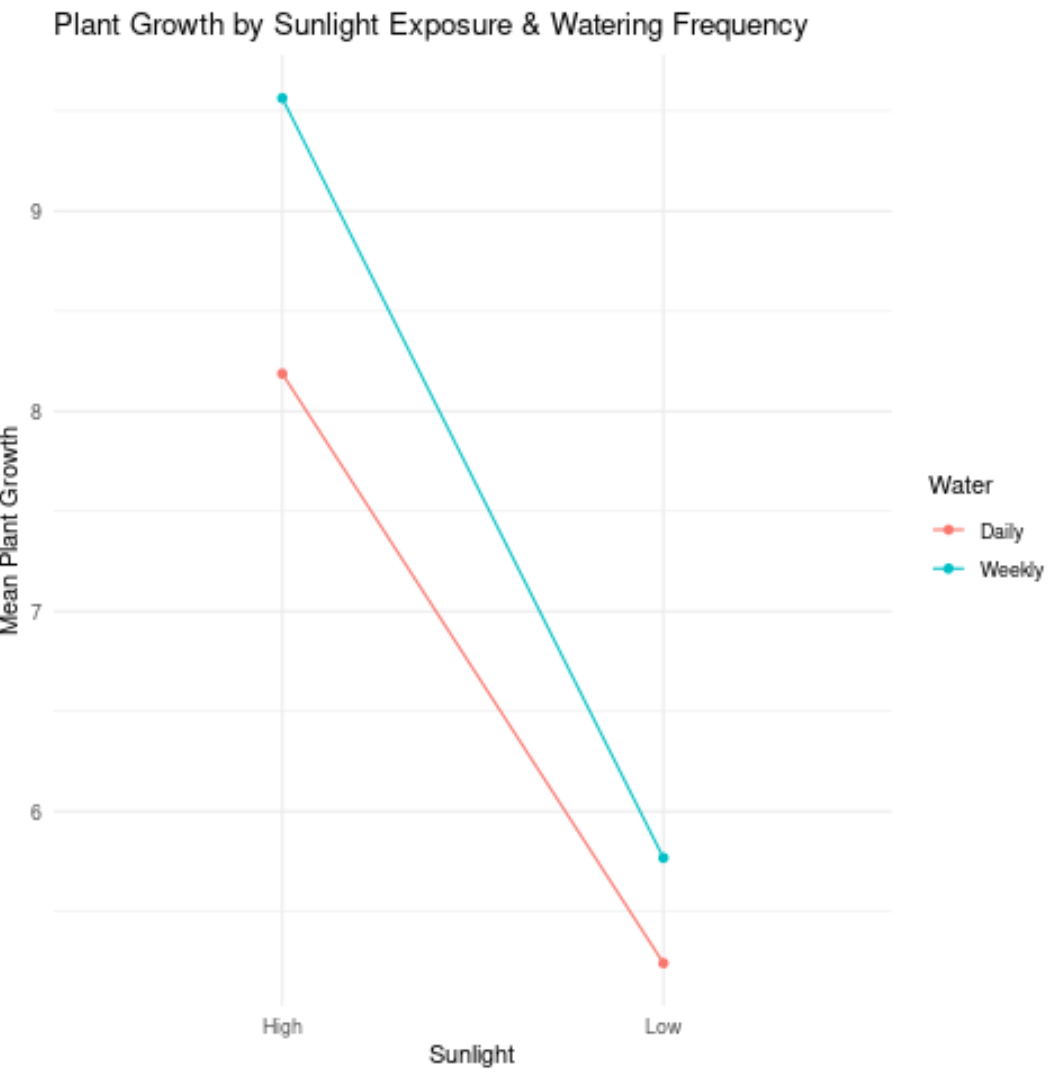
Oto jak interpretować wartości na wykresie:

• Średni wzrost roślin, które otrzymały intensywne światło słoneczne i codzienne podlewanie, wynosił około 20,2 cala.
• Średni wzrost roślin otrzymujących duże nasłonecznienie i cotygodniowe podlewanie wynosił około 30 cm.
• Średni wzrost roślin, które otrzymywały niskie nasłonecznienie i codzienne podlewanie, wynosił około 15,3 cala.
• Średni wzrost roślin, które otrzymywały niskie nasłonecznienie i cotygodniowe podlewanie, wynosił około 15,8 cala.

Aby określić, czy istnieje efekt interakcji pomiędzy dwiema niezależnymi zmiennymi, po prostu sprawdź, czy linie są równoległe, czy nie:

• Jeśli dwie linie wykresu są równoległe, nie ma efektu interakcji.
• Jeśli dwie linie wykresu nie są równoległe, występuje efekt interakcji.

Na poprzednim wykresie obie linie były mniej więcej równoległe, więc prawdopodobnie nie ma efektu interakcji pomiędzy częstotliwością podlewania a ekspozycją na słońce.

Rozważ jednak następujący wykres:

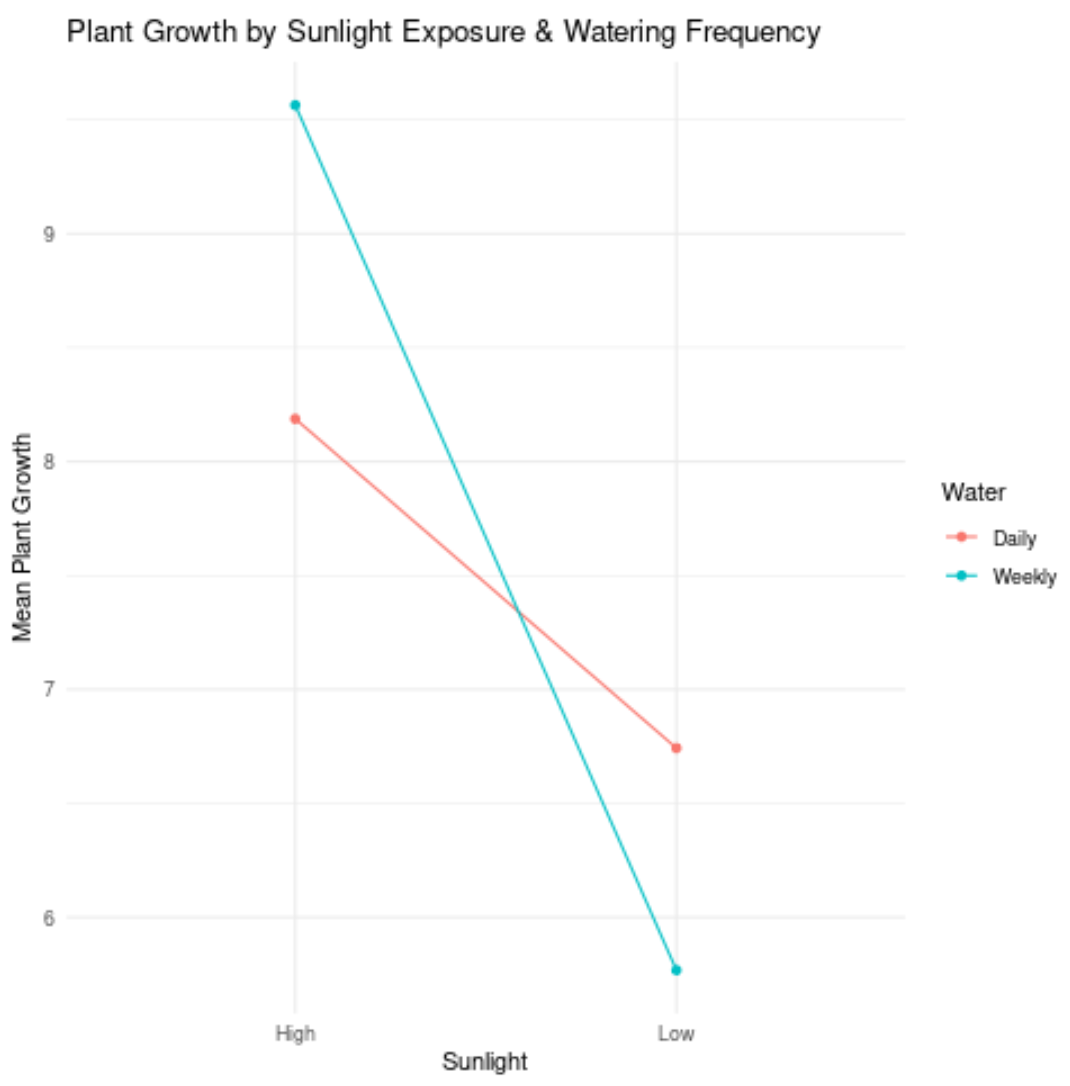
Obie linie wcale nie są równoległe (a właściwie przecinają się!), co wskazuje, że prawdopodobnie zachodzi między nimi efekt interakcji.

Oznacza to na przykład, że wpływ światła słonecznego na wzrost roślin zależy od częstotliwości podlewania.

Innymi słowy, światło słoneczne i częstotliwość podlewania nie wpływają niezależnie na wzrost roślin. Przeciwnie, istnieje efekt interakcji pomiędzy dwiema niezależnymi zmiennymi.

Jak analizować projekt czynnikowy 2×2

Wykreślanie średnich to wizualny sposób sprawdzenia wpływu zmiennych niezależnych na zmienną zależną.

Możemy jednak również przeprowadzić dwuczynnikową analizę ANOVA , aby formalnie sprawdzić, czy zmienne niezależne mają statystycznie istotny związek ze zmienną zależną.

Na przykład poniższy kod pokazuje, jak przeprowadzić dwukierunkową analizę ANOVA dla naszego hipotetycznego scenariusza fabryki w R:

 #make this example reproducible
set. seeds (0)

df <- data. frame (sunlight = rep(c(' Low ', ' High '), each = 30 ),
                 water = rep(c(' Daily ', ' Weekly '), each = 15 , times = 2 ),
                 growth = c(rnorm(15, 6, 2), rnorm(15, 7, 3), rnorm(15, 7, 2),
                                   rnorm(15, 10, 3)))

#fit the two-way ANOVA model
model <- aov(growth ~ sunlight * water, data = df)

#view the model output
summary(model)

               Df Sum Sq Mean Sq F value Pr(>F)   
sunlight 1 52.5 52.48 8.440 0.00525 **
water 1 31.6 31.59 5.081 0.02813 * 
sunlight:water 1 12.8 12.85 2.066 0.15620   
Residuals 56 348.2 6.22                   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Oto jak interpretować wynik ANOVA:

• Wartość p związana ze światłem słonecznym wynosi 0,005 . Ponieważ liczba ta jest mniejsza niż 0,05, oznacza to, że ekspozycja na światło słoneczne ma statystycznie istotny wpływ na wzrost roślin.
• Wartość p związana z wodą wynosi 0,028 . Ponieważ liczba ta jest mniejsza niż 0,05, oznacza to, że częstotliwość podlewania ma również statystycznie istotny wpływ na wzrost roślin.
• Wartość p dla interakcji światła słonecznego i wody wynosi 0,156 . Ponieważ liczba ta jest nie mniejsza niż 0,05, oznacza to, że nie ma efektu interakcji pomiędzy światłem słonecznym a wodą.

Dodatkowe zasoby

Kompletny przewodnik: projekt czynnikowy 2 × 3
Jakie są poziomy zmiennej niezależnej?
Zmienne niezależne lub zależne
Co to jest silnia ANOVA?