Częstotliwość skumulowana
W tym artykule wyjaśniono, jaka jest skumulowana częstotliwość w statystykach. W ten sposób dowiesz się, co oznacza częstotliwość skumulowana, jak obliczana jest częstotliwość skumulowana na przykładach i wreszcie, jakie istnieją rodzaje częstotliwości skumulowanych.
Co to jest częstotliwość skumulowana?
W statystyce częstotliwość skumulowana to skumulowana suma częstotliwości. Oznacza to, że skumulowana częstotliwość wartości jest równa częstotliwości tej wartości plus częstotliwości wszystkich niższych wartości.
Istnieją dwa rodzaje częstotliwości skumulowanych: skumulowana częstotliwość bezwzględna i skumulowana częstotliwość względna. Poniżej zobaczymy, jak obliczany jest każdy typ częstotliwości skumulowanej.
Należy pamiętać, że aby zrozumieć, co oznacza częstotliwość skumulowana w statystykach, należy najpierw mieć jasność co do pojęcia częstotliwości. Dlatego przed kontynuowaniem wyjaśnień zaleca się zapoznanie z następującym postem:
Jak obliczyć częstotliwość skumulowaną
Aby obliczyć skumulowaną częstotliwość próby statystycznej, należy wykonać następujące kroki:
- Utwórz tabelę ze wszystkimi różnymi wartościami pojawiającymi się w zestawie danych, uporządkowanymi od najmniejszej do największej.
- Znajdź częstotliwość bezwzględną każdej wartości.
- Znajdź skumulowaną częstotliwość każdej wartości, którą oblicza się, dodając częstotliwość samej wartości i częstotliwości wszystkich mniejszych wartości.
Dlatego wzór na obliczenie częstotliwości skumulowanej jest następujący:
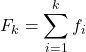
Złoto:
-
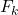
jest skumulowaną częstotliwością wartości

.
-

jest częstotliwością bezwzględną wartości

.
Należy zauważyć, że te kroki służą do obliczenia skumulowanej częstotliwości bezwzględnej, ale istnieje również skumulowana częstotliwość względna. Poniżej zobaczymy różnicę między tymi dwoma typami skumulowanych częstotliwości oraz sposób znajdowania każdego typu.
Rodzaje częstotliwości skumulowanych
W statystyce istnieją dwa rodzaje częstotliwości skumulowanych :
- Skumulowana częstotliwość bezwzględna : jest to skumulowana suma częstotliwości bezwzględnych .
- Skumulowana częstotliwość względna : jest to skumulowana suma częstotliwości względnych .
Biorąc pod uwagę definicję każdego rodzaju skumulowanej częstotliwości, poniżej można zobaczyć przykład sposobu uzyskiwania każdego z nich.
Skumulowana częstotliwość bezwzględna
Skumulowana częstotliwość bezwzględna jest reprezentowana przez symbol Fi i jest obliczana poprzez dodanie częstotliwości bezwzględnych wartości równych lub mniejszych od danej wartości. Następnie mamy konkretny przykład, w którym obliczana jest skumulowana częstotliwość bezwzględna zbioru danych statystycznych.
- Oceny uzyskane z przedmiotu statystyka w klasie 30 uczniów przedstawiają się następująco. Jaka jest skumulowana częstotliwość bezwzględna każdej nuty?
![]()
![]()
![]()
Ponieważ wszystkie liczby mogą być tylko liczbami całkowitymi, jest to zmienna dyskretna. Nie jest zatem konieczne grupowanie danych w przedziały.
Aby więc określić skumulowaną częstotliwość bezwzględną, musimy najpierw znaleźć częstotliwość bezwzględną każdej wartości, czyli liczbę wystąpień każdej wartości w próbce statystycznej.

Teraz, gdy znamy częstotliwość bezwzględną każdej wartości, możemy obliczyć ich skumulowane częstotliwości bezwzględne. Aby to zrobić, mamy dwie możliwości: albo dodajemy częstotliwość bezwzględną wartości plus wszystkie częstotliwości bezwzględne najmniejszych wartości, albo odwrotnie, dodajemy częstotliwość bezwzględną wartości plus skumulowaną częstotliwość bezwzględną poprzednich wartości . wartość.

W skrócie tabela z bezwzględną skumulowaną częstotliwością ćwiczeń wygląda następująco:

Należy pamiętać, że skumulowana częstotliwość bezwzględna ostatniej wartości zawsze pokrywa się z całkowitą liczbą danych. W przeciwnym razie oznacza to, że popełniłeś błąd w obliczeniach.
Skumulowana częstotliwość względna
Skumulowana częstotliwość względna jest reprezentowana przez symbol H i i jest obliczana poprzez dodanie względnych częstotliwości wartości równych lub mniejszych od danej wartości. Poniżej możesz zobaczyć ćwiczenie rozwiązane z tymi samymi danymi, co poprzednie zadanie, w którym wyznaczana jest skumulowana częstotliwość względna.
- Oceny uzyskane ze statystyki w klasie 30 uczniów przedstawiają się następująco. Jaka jest skumulowana względna częstotliwość każdej nuty?
![]()
![]()
![]()
W tym przypadku zmienna jest dyskretna, ponieważ nie może przyjmować wartości dziesiętnej. Nie ma więc potrzeby grupowania danych według przedziałów, ale możemy wykonać obliczenia bezpośrednio.
Dlatego sporządzamy tabelę częstości i określamy częstotliwość bezwzględną każdej innej wartości:

Następnie obliczamy względną częstotliwość każdej wartości, którą wyznaczamy dzieląc częstotliwość bezwzględną przez całkowitą liczbę obserwacji (30).

Kiedy obliczymy częstotliwość bezwzględną i częstotliwość względną zbioru danych, możemy uzyskać skumulowaną częstotliwość względną. Aby to zrobić, należy dodać częstotliwość względną danej wartości plus wszystkie poprzednie częstotliwości względne lub, co sprowadza się do tego samego, poprzednią skumulowaną częstotliwość względną:

Krótko mówiąc, tabela częstotliwości z częstotliwością bezwzględną, częstotliwością względną i skumulowaną częstotliwością względną wygląda następująco:

Pamiętaj, że ostatnia wartość skumulowanej częstotliwości względnej powinna zawsze wynosić 1. Jeśli otrzymasz inną liczbę, oznacza to, że popełniłeś błąd w obliczeniach.