Dlaczego mediana jest ważna w statystyce?
Mediana reprezentuje środkową wartość zbioru danych, gdy wszystkie wartości są uporządkowane od najmniejszej do największej.
Na przykład mediana w następującym zbiorze danych wynosi 19:
Zbiór danych: 3, 4, 11, 15, 19 , 22, 23, 23, 26
Mediana reprezentuje również 50. percentyl zbioru danych. Oznacza to, że dokładnie połowa wartości w zbiorze danych znajduje się powyżej mediany, a połowa wartości poniżej.
Mediana jest ważną metryką do obliczenia, ponieważ daje nam wyobrażenie o tym, gdzie znajduje się „środek” zbioru danych. Daje nam to również wyobrażenie o „typowej” wartości w danym zbiorze danych.
Załóżmy na przykład, że mamy zbiór danych zawierający ceny sprzedaży 10 000 różnych domów w określonym mieście.

Zamiast przeglądać rzędy surowych danych , możemy obliczyć wartość mediany, aby szybko poznać średnią cenę sprzedaży domów w danym mieście.
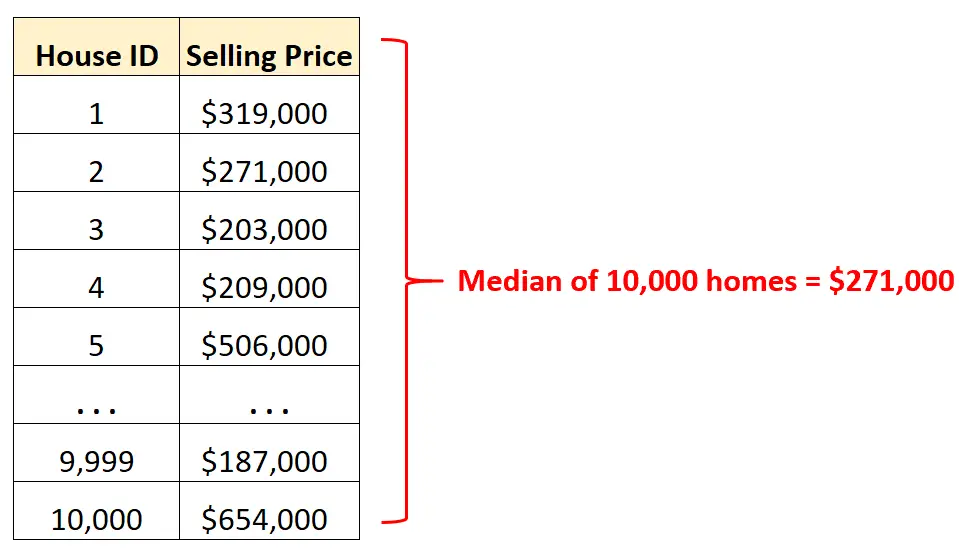
Wiedząc, że średnia cena sprzedaży wynosi 271 000 dolarów, wiemy, że dokładnie połowa z 10 000 domów została sprzedana za kwotę wyższą, a druga połowa za niższą.
Daje nam to również pojęcie o „typowej” cenie sprzedaży domów w tym mieście.
Kiedy stosować medianę
Analizując zbiory danych, często chcemy zrozumieć, gdzie leży główna wartość.
W statystyce istnieją dwie popularne metryki, których używamy do pomiaru środka zbioru danych:
- Średnia : średnia wartość w zestawie danych
- Mediana : mediana wartości w zestawie danych
Okazuje się, że mediana jest bardziej przydatną miarą w następujących okolicznościach:
- Gdy rozkład jest asymetryczny .
- Gdy rozkład zawiera wartości odstające.
Aby to zilustrować, rozważmy dwa poniższe przykłady.
Przykład 1: Obliczanie mediany rozkładu skośnego
Rozważmy następujący rozkład wynagrodzeń mieszkańców danego miasta:

Mediana lepiej oddaje „typową” pensję mieszkańca niż średnia, ponieważ rozkład jest przesunięty w prawo.
Oznacza to, że wysokie płace po prawej stronie rozkładu wypychają średnią z centrum rozkładu.
W tym konkretnym przykładzie średnia pensja wynosi 47 000 dolarów, podczas gdy mediana wynagrodzenia wynosi 32 000 dolarów. Mediana jest znacznie bardziej reprezentatywna dla typowego wynagrodzenia w tym mieście.
Przykład 2: Obliczanie mediany w obecności wartości odstających
Rozważ poniższy wykres przedstawiający powierzchnię domów przy określonej ulicy:

Na średnią duży wpływ ma kilka niezwykle dużych domów, podczas gdy na medianę nie.
Widzimy, że mediana lepiej oddaje „typową” powierzchnię domu przy tej ulicy niż średnia, ponieważ nie mają na nią wpływu wartości odstające.
Streszczenie
Oto krótkie podsumowanie głównych punktów poruszonych w tym artykule:
- Mediana reprezentuje środkową wartość w zbiorze danych.
- Mediana jest ważna, ponieważ daje nam wyobrażenie o tym, gdzie w zbiorze danych znajduje się wartość środkowa.
- Mediana jest zwykle bardziej użyteczna do obliczeń niż średnia, gdy rozkład jest skośny i/lub zawiera wartości odstające.
Dodatkowe zasoby
Konkretne przykłady: użycie średniej, mediany i trybu
Kiedy stosować średnią vs. Mediana: z przykładami
Dlaczego tryb jest ważny w statystykach?