Dlaczego wielkość próbki jest ważna? (wyjaśnienie i przykłady)
Wielkość próby odnosi się do całkowitej liczby osób biorących udział w eksperymencie lub badaniu.
Wielkość próby jest istotna, ponieważ bezpośrednio wpływa na precyzję, z jaką możemy oszacować parametry populacji.
Aby zrozumieć, dlaczego tak się dzieje, pomocna jest podstawowa wiedza na temat przedziałów ufności.
Krótkie wyjaśnienie przedziałów ufności
W statystyce często staramy się mierzyć parametry populacji – liczby opisujące pewne cechy całej populacji.
Na przykład możemy być zainteresowani pomiarem średniego wzrostu wszystkich osób w określonym mieście.
Jednakże gromadzenie danych na temat każdego osobnika w populacji jest często zbyt kosztowne i czasochłonne. Zwykle więc pobieramy losową próbkę z populacji i wykorzystujemy próbne dane do oszacowania parametru populacji.
Na przykład moglibyśmy zebrać dane na temat wzrostu 100 przypadkowych osób w mieście. Następnie możemy obliczyć średnią wielkość osobników w próbie. Nie możemy jednak mieć pewności, że średnia próbki dokładnie odpowiada średniej populacji.
Aby uwzględnić tę niepewność, możemy utworzyć przedział ufności . Przedział ufności to zakres wartości, który prawdopodobnie będzie zawierał parametr populacji z pewnym poziomem ufności.
Wzór na obliczenie przedziału ufności dla średniej populacji jest następujący:
Przedział ufności = x +/- z*(s/√ n )
Złoto:
- x : przykładowe środki
- z: wybrana wartość z
- s: odchylenie standardowe próbki
- n: wielkość próbki
Używana wartość z zależy od wybranego poziomu ufności. W poniższej tabeli przedstawiono wartość z odpowiadającą najczęściej wybieranym poziomom ufności:
| Poziom pewności | wartość z |
|---|---|
| 0,90 | 1645 |
| 0,95 | 1,96 |
| 0,99 | 2,58 |
Zależność między wielkością próby a przedziałami ufności
Załóżmy, że chcemy oszacować średnią masę populacji żółwi. Pobieramy losową próbkę żółwi z następującymi informacjami:
- Wielkość próby n = 25
- Średnia masa próbki x = 300
- Próbka odchylenie standardowe s = 18,5
Oto jak obliczyć 90% przedział ufności dla prawdziwej średniej wagi populacji:
90% przedział ufności: 300 +/- 1,645*(18,5/√ 25 ) = [293,91, 306,09]
Jesteśmy w 90% pewni, że rzeczywista średnia waga żółwi w populacji wynosi od 293,91 do 306,09 funtów.
Załóżmy teraz, że zamiast 25 żółwi zbieramy dane o 50 żółwiach.
Oto jak obliczyć 90% przedział ufności dla prawdziwej średniej wagi populacji:
90% przedział ufności: 300 +/- 1,645*(18,5/√ 50 ) = [295,79, 304,30]
Należy zauważyć, że ten przedział ufności jest węższy niż poprzedni przedział ufności. Oznacza to, że nasze oszacowanie prawdziwej średniej masy populacji żółwi jest dokładniejsze.
Załóżmy teraz, że zbieramy dane o 100 żółwiach.
Oto jak obliczyć 90% przedział ufności dla prawdziwej średniej wagi populacji:
90% przedział ufności: 300 +/- 1,645*(18,5/√ 100 ) = [296,96, 303,04]
Należy zauważyć, że ten przedział ufności jest jeszcze węższy niż poprzedni przedział ufności.
Poniższa tabela podsumowuje każdą szerokość przedziału ufności:
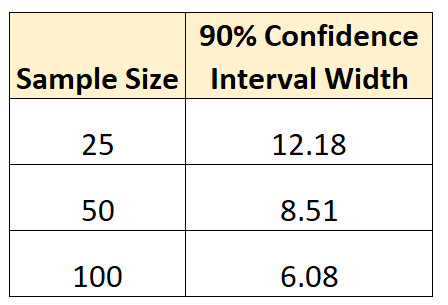
Konkluzja jest następująca: im większa wielkość próby, tym dokładniej możemy oszacować parametr populacji .
Dodatkowe zasoby
Poniższe samouczki zawierają bardziej przydatne wyjaśnienia dotyczące przedziałów ufności i wielkości próby.
Wprowadzenie do przedziałów ufności
4 Przykłady przedziałów ufności w prawdziwym życiu
Populacja vs. próbka: jaka jest różnica?