Dlaczego odchylenie standardowe jest ważne? (wyjaśnienie + przykłady)

Odchylenie standardowe służy do pomiaru rozkładu wartości w próbce.

Do obliczenia odchylenia standardowego danej próbki możemy posłużyć się następującym wzorem:

√ Σ(x _i – x _bar ) ² / (n-1)

Złoto:

• Σ: Symbol oznaczający „sumę”
• x _i : ^i-ta wartość próbki
• x _słupek : Oznacza próbkę
• n: Wielkość próbki

Im wyższa wartość odchylenia standardowego, tym bardziej rozproszone są wartości w próbce. I odwrotnie, im niższa wartość odchylenia standardowego, tym bardziej wartości są skupione.

Pytanie, które często zadają uczniowie, brzmi: Dlaczego odchylenie standardowe jest ważne?

Odpowiedź: Odchylenie standardowe jest ważne, ponieważ mówi nam o rozkładzie wartości w danym zbiorze danych.

analizujemy zbiór danych Ilekroć chcemy znaleźć następujące metryki:

• Centrum zbioru danych . Najczęstszym sposobem pomiaru „środka” jest użycie średniej i mediany.
• Rozkład wartości w zbiorze danych . Najczęstszym sposobem pomiaru spreadu jest użycie odchylenia standardowego.

Wiedząc, gdzie jest centrum i jaki jest rozkład wartości, możemy dobrze zrozumieć rozkład wartości w dowolnym zbiorze danych.

Poniższe przykłady ilustrują znaczenie odchylenia standardowego w praktyce.

Przykład 1: Podział wynagrodzeń

Załóżmy, że średnia pensja w firmie A wynosi 80 000 dolarów, a odchylenie standardowe wynosi 20 000 dolarów. Ponieważ odchylenie standardowe jest tak duże, nie ma gwarancji, że pracując w tej firmie, będziesz otrzymywać wynagrodzenie w wysokości blisko 80 000 dolarów rocznie, ponieważ istnieją duże różnice w wynagrodzeniach.

I odwrotnie, załóżmy, że średnia pensja w firmie B również wynosi 80 000 dolarów, ale odchylenie standardowe wynosi tylko 4000 dolarów. Ponieważ to odchylenie standardowe jest tak małe, możesz być pewien, że otrzymasz wynagrodzenie w wysokości blisko 80 000 dolarów, ponieważ różnice w wynagrodzeniach są bardzo niewielkie.

Gdybyśmy stworzyli wykres pudełkowy w celu wizualizacji rozkładu wynagrodzeń w tych dwóch firmach, mógłby wyglądać następująco:

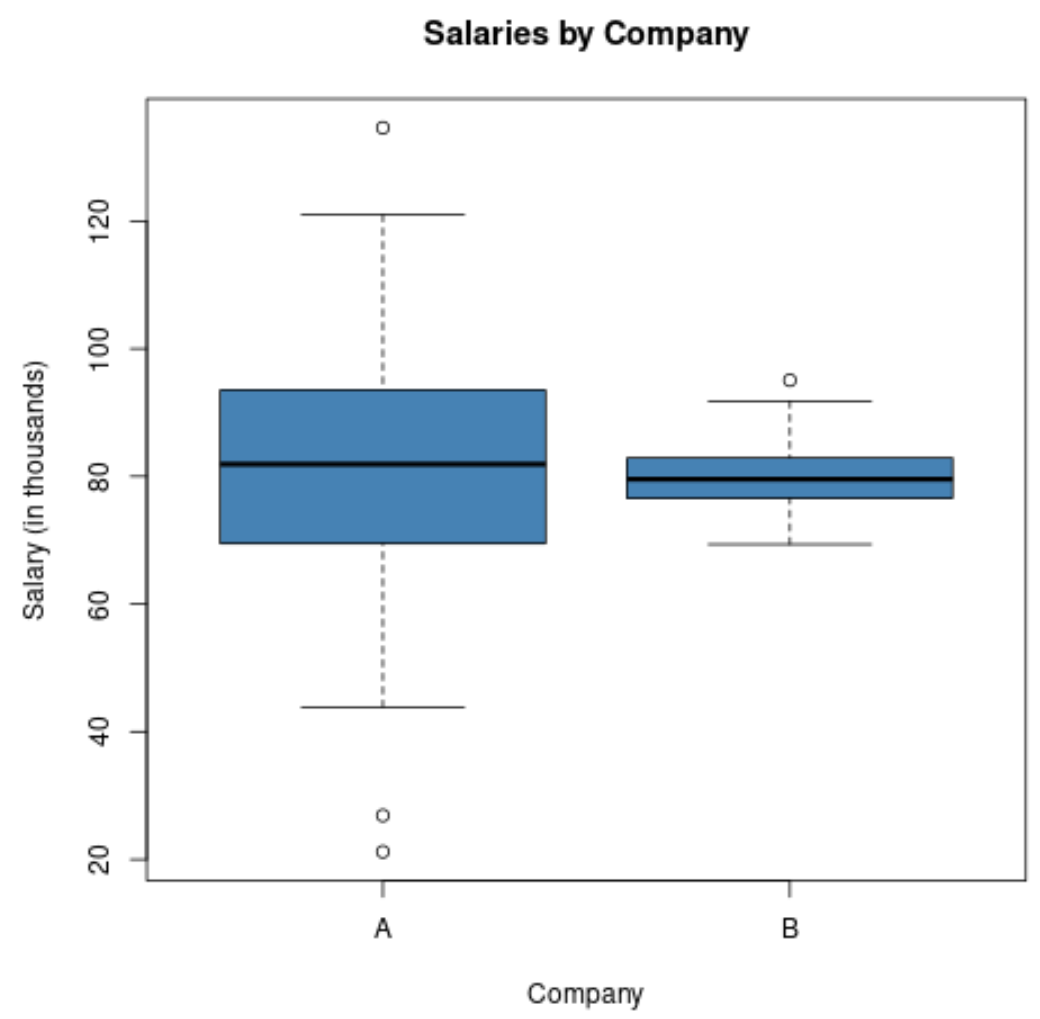
Należy zauważyć, że długość wykresu pudełkowego dla firmy A jest większa, ponieważ odchylenie standardowe płac jest znacznie większe.

Obie firmy mają tę samą średnią pensję, ale różnica w wynagrodzeniach jest znacznie większa w firmie A.

Przykład 2: Rozkład cen mieszkań

Załóżmy, że średnia cena mieszkania w sąsiedztwie A wynosi 250 000 dolarów, a odchylenie standardowe wynosi 50 000 dolarów. Ponieważ odchylenie standardowe jest dość duże, oznacza to, że niektóre ceny domów będą znacznie wyższe niż 250 000 dolarów, a inne będą znacznie niższe. Jeśli spojrzysz na dowolny dom w tej okolicy, nie ma gwarancji, że cena będzie zbliżona do średniej.

I odwrotnie, załóżmy, że średnia cena domu w sąsiedztwie B również wynosi 250 000 dolarów, ale odchylenie standardowe wynosi tylko 10 000 dolarów. Ponieważ to odchylenie standardowe jest dość małe, możesz być pewien, że każdy dom, który zobaczysz w okolicy, prawdopodobnie będzie zamknięty na tę cenę.

Gdybyśmy stworzyli wykres pudełkowy, aby zwizualizować rozkład cen domów w tych dwóch dzielnicach, mógłby wyglądać następująco:

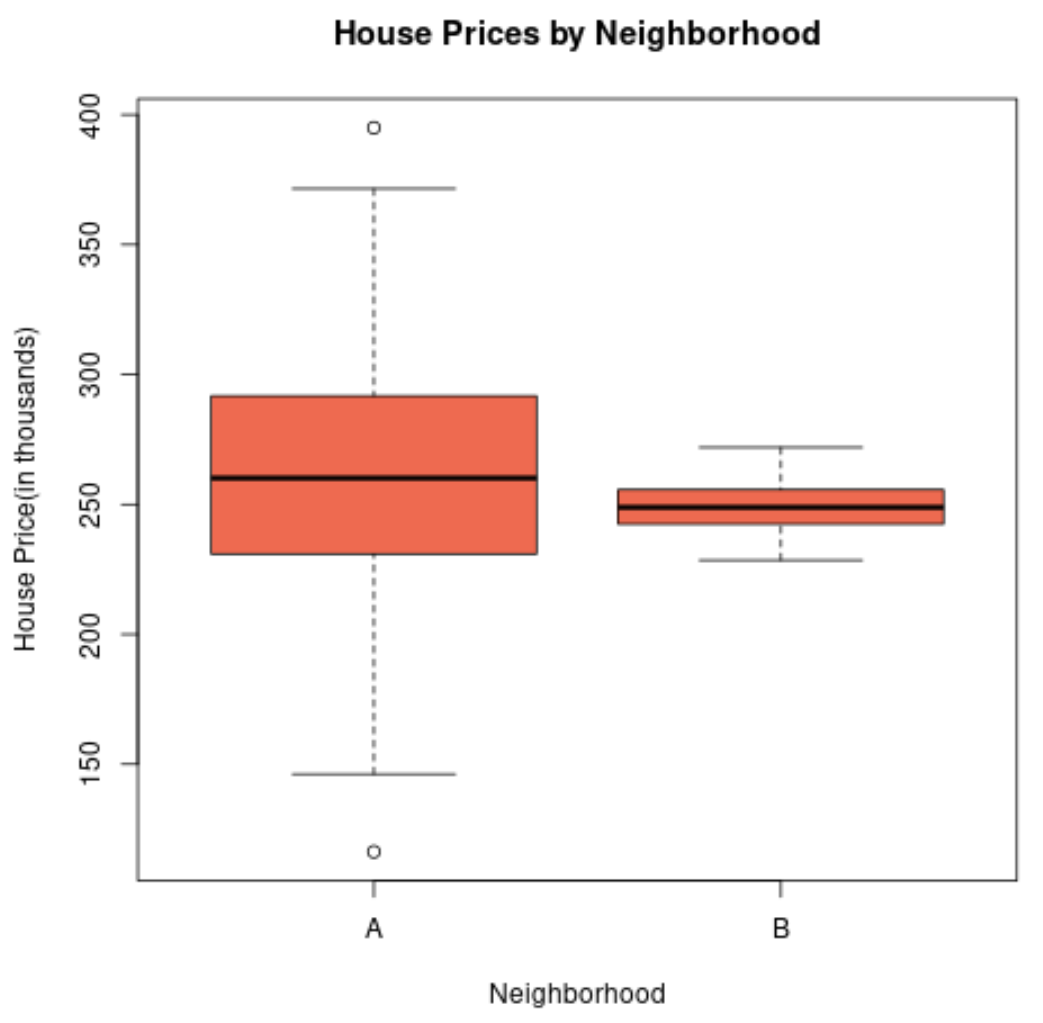
Długość wykresu pudełkowego sąsiedztwa A jest większa, ponieważ odchylenie standardowe cen nieruchomości jest znacznie większe.

W rzeczywistości ceny mieszkań wahają się od mniej niż 150 000 dolarów do ponad 400 000 dolarów w dzielnicy A, podczas gdy ceny wahają się tylko od około 230 000 do 270 000 dolarów w dzielnicy B.

Znając odchylenie standardowe cen domów w każdej okolicy, możemy wiedzieć, jakiego zróżnicowania można się spodziewać w cenach w każdej dzielnicy.

Dodatkowe zasoby

Co uważa się za dobre odchylenie standardowe?
Zasięg vs. Odchylenie standardowe: kiedy używać każdego z nich
Współczynnik zmienności a odchylenie standardowe: różnica