Regresja logistyczna a regresja liniowa: główne różnice

Dwa z najczęściej stosowanych modeli regresji to regresja liniowa i regresja logistyczna .

Obydwa typy modeli regresji służą do ilościowego określenia związku między jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi , ale istnieje kilka kluczowych różnic między tymi dwoma modelami:

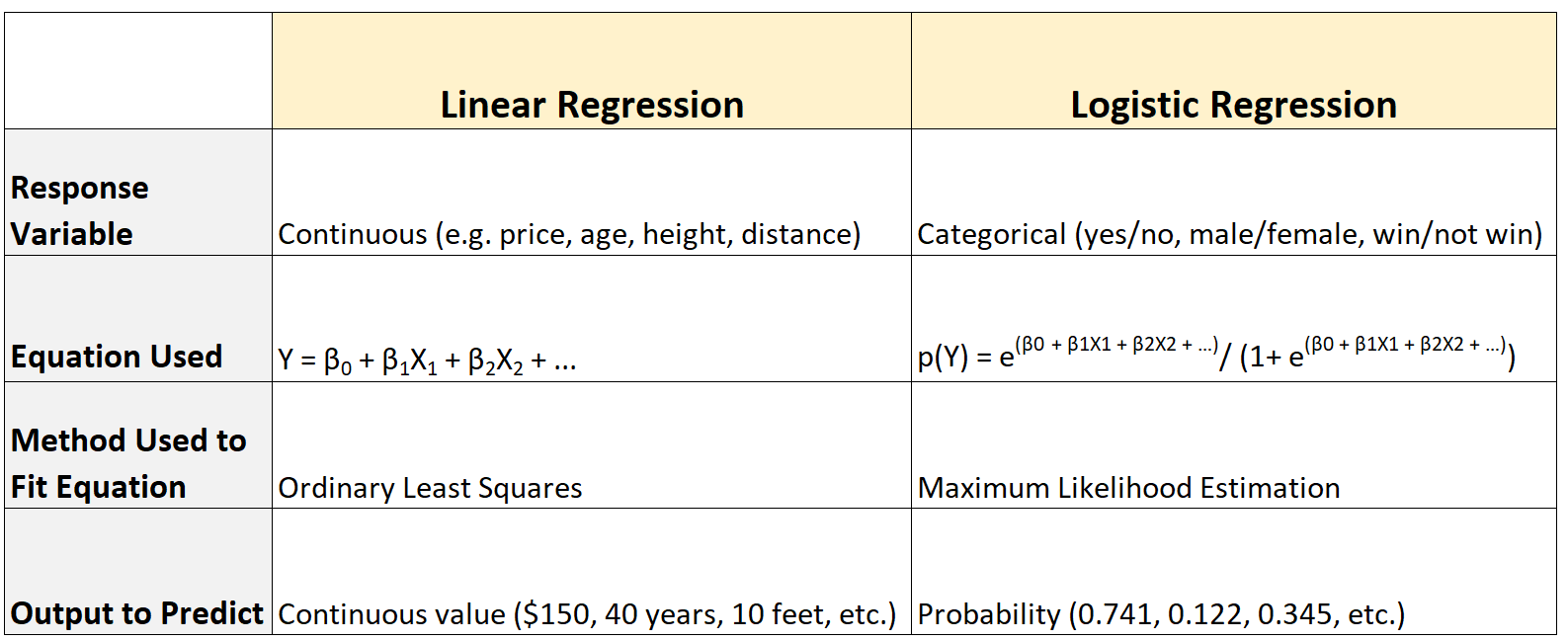
Oto podsumowanie różnic:

Różnica nr 1: Typ zmiennej odpowiedzi

Model regresji liniowej stosuje się, gdy zmienna odpowiedzi przyjmuje wartość ciągłą, taką że:

• Cena
• Wysokość
• Wiek
• Dystans

I odwrotnie, model regresji logistycznej jest używany, gdy zmienna odpowiedzi przyjmuje wartość kategoryczną, taką jak:

• Tak lub nie
• Mężczyzna czy kobieta
• Wygrać czy nie wygrać

Różnica nr 2: użyte równanie

Regresja liniowa wykorzystuje następujące równanie do podsumowania związku między zmiennymi predykcyjnymi a zmienną odpowiedzi:

Y = β ₀ + β ₁ X _{1 +} β ₂ X ₂ + … + β _p

Złoto:

• Y: zmienna odpowiedzi
• X _j : j- ^ta zmienna predykcyjna
• β _j : Średni wpływ na Y jednojednostkowego wzrostu X _j , przy założeniu, że wszystkie inne predyktory są stałe

Odwrotnie, regresja logistyczna wykorzystuje następujące równanie:

p(X) = e ^{β ₀ + _{β 1 X 1 + β 2 X 2 + … + β}} p

Równanie to służy do przewidywania prawdopodobieństwa, że pojedyncza obserwacja należy do określonej kategorii.

Różnica nr 3: Metoda dopasowania równania

W regresji liniowej do znalezienia najlepiej dopasowanego równania regresji wykorzystuje się metodę zwaną zwykłą metodą najmniejszych kwadratów .

Z drugiej strony regresja logistyczna wykorzystuje metodę zwaną estymacją największej wiarygodności w celu znalezienia najlepiej dopasowanego równania regresji.

Różnica nr 4: wynik do przewidzenia

Regresja liniowa przewiduje ciągłą wartość jako wynik. Na przykład:

• Cena (150 USD, 199 USD, 400 USD itd.)
• Wysokość (14 cali, 2 stopy, 94,32 centymetra itp.)
• Wiek (2 miesiące, 6 lat, 41,5 lat itd.)
• Odległość (1,23 mil, 4,5 km itp.)

I odwrotnie, regresja logistyczna przewiduje prawdopodobieństwo jako wynik. Na przykład:

• 40,3% szans na przyjęcie na uniwersytet.
• 93,2% szans na wygraną w grze.
• 34,2% szans na przyjęcie ustawy.

Kiedy stosować regresję logistyczną czy liniową

Poniższe problemy praktyczne mogą pomóc Ci lepiej zrozumieć, kiedy stosować regresję logistyczną, a kiedy regresję liniową.

Problem nr 1: Roczny dochód

Załóżmy, że ekonomista chce wykorzystać zmienne predykcyjne (1) przepracowane godziny w tygodniu i (2) lata edukacji, aby przewidzieć roczny dochód jednostek.

W tym scenariuszu zastosowałby regresję liniową , ponieważ zmienna odpowiedzi (dochód roczny) ma charakter ciągły.

Problem nr 2: Akceptacja uczelni

Załóżmy, że urzędnik ds. rekrutacji na studia chce wykorzystać zmienne predykcyjne (1) GPA i (2) wynik ACT, aby przewidzieć prawdopodobieństwo przyjęcia studenta na określoną uczelnię.

W tym scenariuszu zastosowałaby regresję logistyczną , ponieważ zmienna odpowiedzi jest kategoryczna i może przyjmować tylko dwie wartości: zaakceptowana lub niezaakceptowana.

Problem nr 3: Ceny nieruchomości

Załóżmy, że agent nieruchomości chce użyć zmiennych predykcyjnych (1) metraż kwadratowy, (2) liczba sypialni i (3) liczba łazienek, aby przewidzieć ceny sprzedaży domów.

W tym scenariuszu zastosowałaby regresję liniową , ponieważ zmienna odpowiedzi (cena) ma charakter ciągły.

Problem nr 4: Wykrywanie spamu

Załóżmy, że programista komputerowy chce użyć zmiennych predykcyjnych (1) liczby słów i (2) kraju pochodzenia, aby przewidzieć prawdopodobieństwo, że dana wiadomość e-mail jest spamem.

W tym scenariuszu zastosowałaby regresję logistyczną , ponieważ zmienna odpowiedzi jest kategoryczna i może przyjmować tylko dwie wartości: spam lub nie spam.

Dodatkowe zasoby

Poniższe samouczki zawierają więcej szczegółów na temat regresji liniowej:

• Wprowadzenie do prostej regresji liniowej
• Wprowadzenie do wielokrotnej regresji liniowej
• 4 przykłady wykorzystania regresji liniowej w prawdziwym życiu

Poniższe samouczki zawierają więcej szczegółów na temat regresji logistycznej:

• Wprowadzenie do regresji logistycznej
• 4 Przykłady wykorzystania regresji logistycznej w życiu codziennym