Jak znaleźć średnią wielu odchyleń standardowych
Czasami możesz chcieć znaleźć średnią z dwóch lub więcej odchyleń standardowych.
W tym celu możesz skorzystać z jednej z dwóch formuł, w zależności od Twoich danych:
Metoda 1: Równa wielkość próbki
Jeśli chcesz znaleźć średnie odchylenie standardowe wśród k grup, a każda grupa ma tę samą wielkość próby, możesz skorzystać z następującego wzoru:
Średnie SD = √ (s 1 2 + s 2 2 + … + s k 2 ) / k
Złoto:
- sk : Odchylenie standardowe dla k-tej grupy
- k : Całkowita liczba grup
Metoda 2: Nierówne wielkości próbek
Jeśli chcesz znaleźć średnie odchylenie standardowe wśród k grup, a każda grupa nie ma tej samej wielkości próby, możesz skorzystać z następującego wzoru:
Średnie SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – J)
Złoto:
- n k : Wielkość próby dla k -tej grupy
- sk : Odchylenie standardowe dla k-tej grupy
- k : Całkowita liczba grup
Poniższe przykłady pokazują, jak zastosować każdą formułę w praktyce.
Metoda 1: Obliczanie średniej odchyleń standardowych dla próbek o jednakowej wielkości
Załóżmy, że chcemy obliczyć średnie odchylenie standardowe sprzedaży w następujących sześciu okresach sprzedaży:
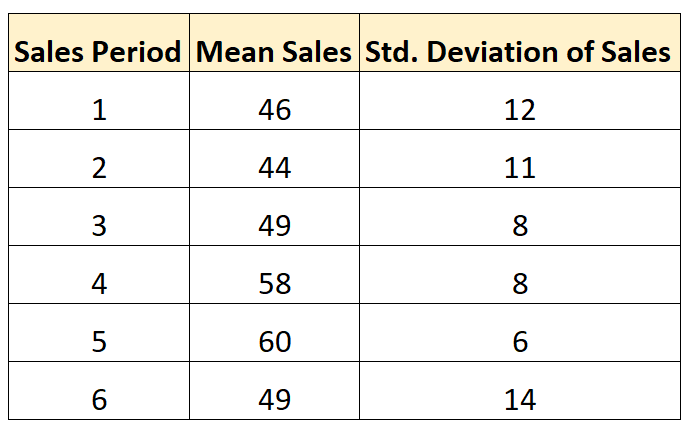
Załóżmy, że w każdym okresie sprzedaży dokonaliśmy tej samej liczby transakcji sprzedaży. Aby obliczyć średnie odchylenie standardowe sprzedaży w danym okresie, możemy skorzystać z poniższego wzoru:
- Średnie odchylenie standardowe = √ (s 1 2 + s 2 2 + … + s k 2 ) / k
- Średnie odchylenie standardowe = √ (12 2 + 11 2 + 8 2 + 8 2 + 6 2 + 14 2 ) / 6
- Średnie odchylenie standardowe = 10,21
Średnie odchylenie standardowe sprzedaży w okresie wynosi 10,21 .
Metoda 2: Uśrednianie odchyleń standardowych dla nierównych wielkości próbek
Załóżmy, że chcemy obliczyć średnie odchylenie standardowe sprzedaży w następujących sześciu okresach sprzedaży:
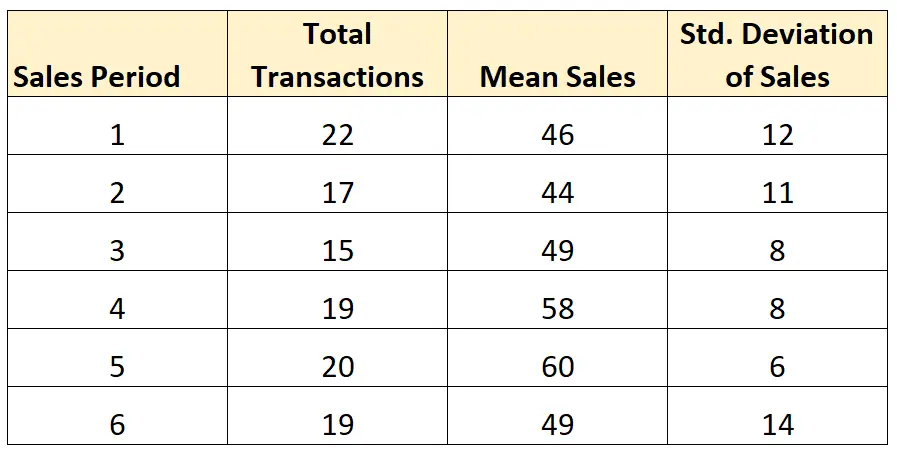
Ponieważ wielkość próby (łączna liczba transakcji) nie jest równa w każdym okresie sprzedaży, do obliczenia średniego odchylenia standardowego sprzedaży w okresie użyjemy następującego wzoru:
- Średnie SD = √ ((n 1 -1)s 1 2 + (n 2 -1)s 2 2 + … + (n k -1)s k 2 ) / (n 1 +n 2 + … + n k – J)
- Średnie SD = √ ((21)12 2 + (16)11 2 + (14)8 2 + (18)8 2 + (19)6 2 + (18)14 2 ) / 106
- Średnia SD = 10,29
Średnie odchylenie standardowe sprzedaży w okresie wynosi 10,29 .
Należy zauważyć, że średnie odchylenie standardowe w obu przykładach było dość podobne. Dzieje się tak dlatego, że wielkości próbek (łączna liczba transakcji) w drugim przykładzie były dość zbliżone do siebie.
Obie metody obliczania średniego odchylenia standardowego różnią się znacząco tylko wtedy, gdy liczebność próbek znacznie różni się między grupami.