Co to jest doskonała wielowspółliniowość? (definicja i przykłady)

W statystyce wieloliniowość występuje, gdy dwie lub więcej zmiennych predykcyjnych jest ze sobą silnie skorelowanych, tak że nie dostarczają unikalnych lub niezależnych informacji w modelu regresji.

Jeśli stopień korelacji między zmiennymi jest wystarczająco wysoki, może to powodować problemy podczas dopasowywania i interpretacji modelu regresji.

Najbardziej ekstremalny przypadek współliniowości nazywany jest doskonałą wielowspółliniowością . Dzieje się tak, gdy dwie lub więcej zmiennych predykcyjnych ma ze sobą dokładnie liniową zależność.

Załóżmy na przykład, że mamy następujący zestaw danych:

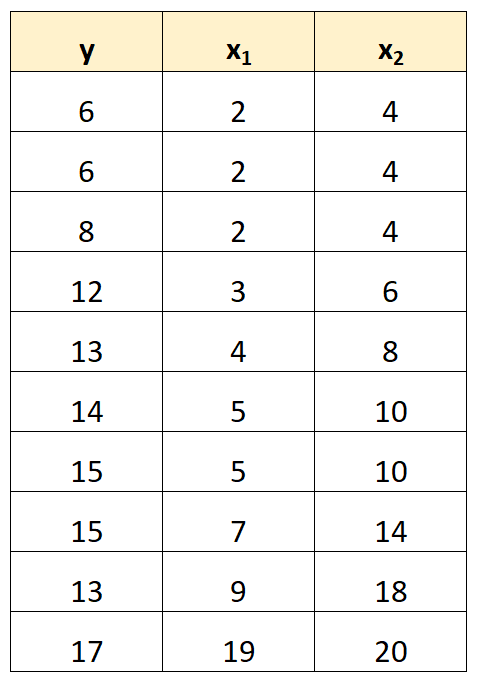
Należy zauważyć, że wartości zmiennej predykcyjnej x ₂ są po prostu wartościami x ₁ pomnożonymi przez 2.

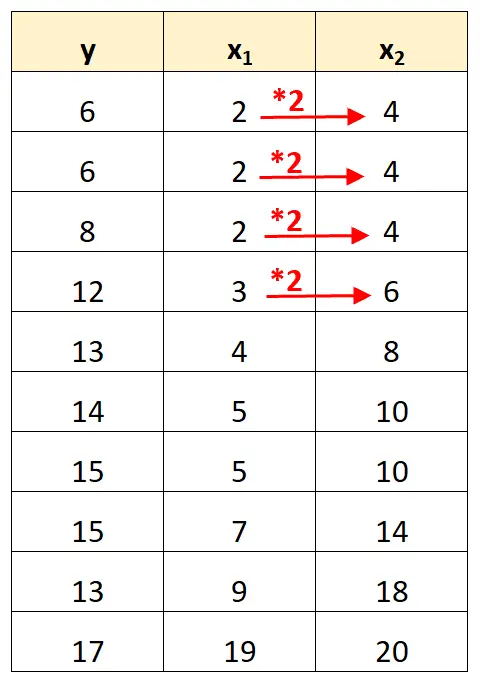
Jest to przykład doskonałej wielowspółliniowości .

Problem doskonałej wielowspółliniowości

Gdy w zbiorze danych występuje doskonała wieloliniowość, zwykła metoda najmniejszych kwadratów nie jest w stanie wygenerować szacunków współczynników regresji.

Rzeczywiście, nie jest możliwe oszacowanie marginalnego wpływu zmiennej predykcyjnej (x ₁ ) na zmienną odpowiedzi (y), przy jednoczesnym utrzymaniu innej zmiennej predykcyjnej (x ₂ ) na stałym poziomie, ponieważ x ₂ porusza się zawsze dokładnie wtedy, gdy porusza się x ₁ .

Krótko mówiąc, idealna współliniowość uniemożliwia oszacowanie wartości każdego współczynnika w modelu regresji.

Jak sobie radzić z doskonałą wielowspółliniowością

Najprostszym sposobem poradzenia sobie z doskonałą współliniowością jest usunięcie jednej ze zmiennych, która ma dokładnie liniową zależność z inną zmienną.

Na przykład w naszym poprzednim zbiorze danych mogliśmy po prostu usunąć x ₂ jako zmienną predykcyjną.

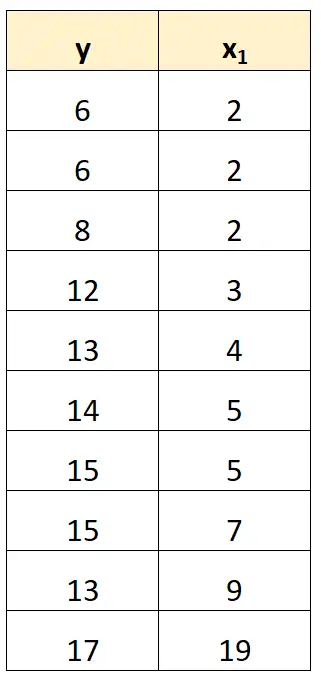
Następnie dopasowalibyśmy model regresji, stosując x ₁ jako zmienną predykcyjną i y jako zmienną odpowiedzi.

Przykłady doskonałej wielowspółliniowości

Poniższe przykłady pokazują trzy najczęstsze scenariusze doskonałej współliniowości w praktyce.

1. Zmienna predykcyjna jest wielokrotnością innej zmiennej

Załóżmy, że chcemy użyć „wzrostu w centymetrach” i „wzrostu w metrach”, aby przewidzieć wagę określonego gatunku delfina.

Tak mógłby wyglądać nasz zbiór danych:

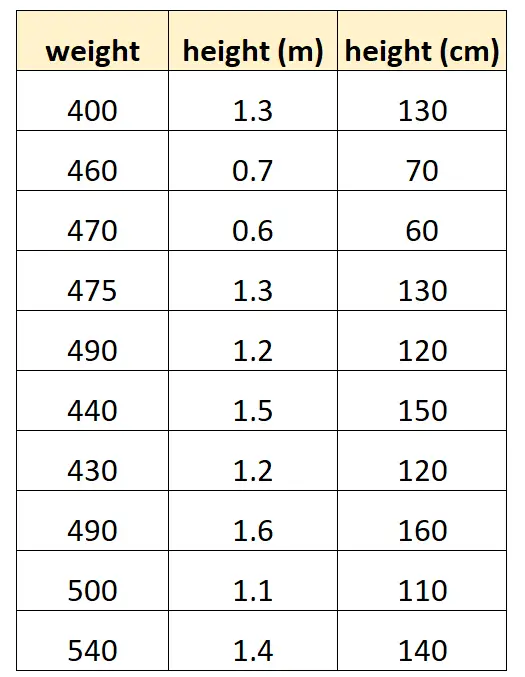
Należy zauważyć, że wartość „wzrostu w centymetrach” jest po prostu równa „wzrostowi w metrach” pomnożonemu przez 100. Jest to przypadek doskonałej współliniowości.

Jeśli spróbujemy dopasować model regresji liniowej w R przy użyciu tego zbioru danych, nie będziemy w stanie wygenerować oszacowania współczynnika dla zmiennej predykcyjnej „metry”:

 #define data
df <- data. frame (weight=c(400, 460, 470, 475, 490, 440, 430, 490, 500, 540),
                 m=c(1.3, .7, .6, 1.3, 1.2, 1.5, 1.2, 1.6, 1.1, 1.4),
                 cm=c(130, 70, 60, 130, 120, 150, 120, 160, 110, 140))

#fit multiple linear regression model
model <- lm(weight~m+cm, data=df)

#view summary of model
summary(model)

Call:
lm(formula = weight ~ m + cm, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-70,501 -25,501 5,183 19,499 68,590 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 458,676 53,403 8,589 2.61e-05 ***
m 9.096 43.473 0.209 0.839    
cm NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 41.9 on 8 degrees of freedom
Multiple R-squared: 0.005442, Adjusted R-squared: -0.1189 
F-statistic: 0.04378 on 1 and 8 DF, p-value: 0.8395

2. Zmienna predykcyjna jest przekształconą wersją innej

Załóżmy, że chcemy użyć „punktów” i „punktów skalowanych” do przewidzenia ocen koszykarzy.

Załóżmy, że zmienna „punkty skalowane” jest obliczana jako:

Punkty skalowane = (punkty – μ _punktów ) / σ _punktów

Tak mógłby wyglądać nasz zbiór danych:

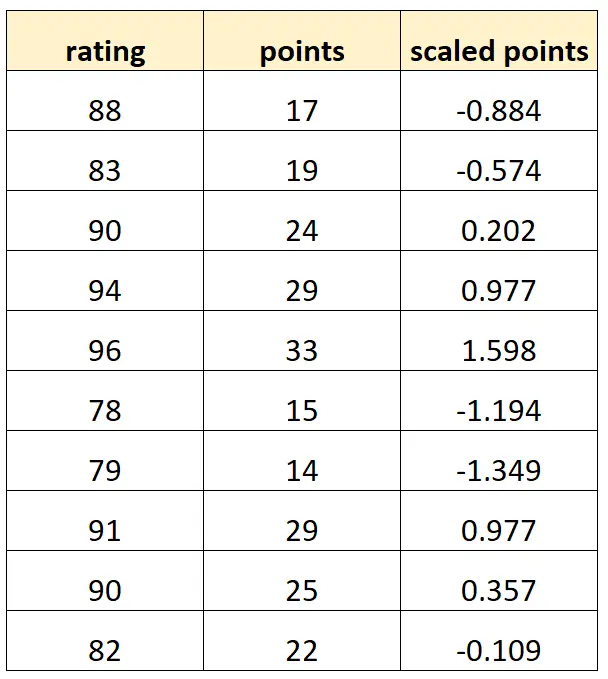
Należy pamiętać, że każda wartość „punktów skalowanych” jest po prostu standardową wersją „punktów”. Jest to przypadek doskonałej wielowspółliniowości.

Jeśli spróbujemy dopasować model regresji liniowej w R przy użyciu tego zbioru danych, nie będziemy w stanie wygenerować oszacowania współczynnika dla zmiennej predykcyjnej „punkty skalowane”:

 #define data
df <- data. frame (rating=c(88, 83, 90, 94, 96, 78, 79, 91, 90, 82),
                 pts=c(17, 19, 24, 29, 33, 15, 14, 29, 25, 22))

df$scaled_pts <- (df$pts - mean(df$pts)) / sd(df$pts)

#fit multiple linear regression model
model <- lm(rating~pts+scaled_pts, data=df)

#view summary of model
summary(model)

Call:
lm(formula = rating ~ pts + scaled_pts, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-4.4932 -1.3941 -0.2935 1.3055 5.8412 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 67.4218 3.5896 18.783 6.67e-08 ***
pts 0.8669 0.1527 5.678 0.000466 ***
scaled_pts NA NA NA NA    
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.953 on 8 degrees of freedom
Multiple R-squared: 0.8012, Adjusted R-squared: 0.7763 
F-statistic: 32.23 on 1 and 8 DF, p-value: 0.0004663

3. Sztuczna pułapka zmienna

Inny scenariusz, w którym może wystąpić doskonała wieloliniowość, nazywany jest fikcyjną pułapką zmiennych . Dzieje się tak wtedy, gdy chcemy wziąć zmienną kategoryczną w modelu regresji i przekształcić ją w „zmienną fikcyjną”, która przyjmuje wartości 0, 1, 2 itd.

Załóżmy na przykład, że chcemy użyć zmiennych predykcyjnych „wiek” i „stan cywilny” do przewidzenia dochodów:

Aby użyć „stanu cywilnego” jako zmiennej predykcyjnej, musimy najpierw przekształcić go w zmienną fikcyjną.

Aby to zrobić, możemy pozostawić „Single” jako wartość bazową, ponieważ zdarza się to najczęściej, i przypisać wartości 0 lub 1 do „Żonaty” i „Rozwód” w następujący sposób:

Błędem byłoby utworzenie trzech nowych zmiennych fikcyjnych w następujący sposób:

W tym przypadku zmienna „Singiel” jest idealną liniową kombinacją zmiennych „Żonaty” i „Rozwiedziony”. Jest to przykład doskonałej wielowspółliniowości.

Jeśli spróbujemy dopasować model regresji liniowej w R przy użyciu tego zbioru danych, nie będziemy w stanie wygenerować oszacowania współczynnika dla każdej zmiennej predykcyjnej:

 #define data
df <- data. frame (income=c(45, 48, 54, 57, 65, 69, 78, 83, 98, 104, 107),
                 age=c(23, 25, 24, 29, 38, 36, 40, 59, 56, 64, 53),
                 single=c(1, 1, 1, 1, 0, 1, 0, 1, 1, 0, 0),
                 married=c(0, 0, 0, 0, 1, 0, 1, 0, 0, 1, 1),
                 divorced=c(0, 0, 0, 0, 0, 0, 0, 1, 1, 0, 0))

#fit multiple linear regression model
model <- lm(income~age+single+married+divorced, data=df)

#view summary of model
summary(model)

Call:
lm(formula = income ~ age + single + married + divorced, data = df)

Residuals:
    Min 1Q Median 3Q Max 
-9.7075 -5.0338 0.0453 3.3904 12.2454 

Coefficients: (1 not defined because of singularities)
            Estimate Std. Error t value Pr(>|t|)   
(Intercept) 16.7559 17.7811 0.942 0.37739   
age 1.4717 0.3544 4.152 0.00428 **
single -2.4797 9.4313 -0.263 0.80018   
married NA NA NA NA   
divorced -8.3974 12.7714 -0.658 0.53187   
---
Significant. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 8.391 on 7 degrees of freedom
Multiple R-squared: 0.9008, Adjusted R-squared: 0.8584 
F-statistic: 21.2 on 3 and 7 DF, p-value: 0.0006865

Dodatkowe zasoby

Przewodnik po wielowspółliniowości i VIF w regresji
Jak obliczyć VIF w R
Jak obliczyć VIF w Pythonie
Jak obliczyć VIF w Excelu