Jak obliczyć przedział ufności dla ryzyka względnego

Ryzyko względne jest często obliczane podczas analizy tabeli 2×2, która ma następujący format:

Ryzyko względne mówi nam o prawdopodobieństwie wystąpienia zdarzenia w grupie badanej w porównaniu z prawdopodobieństwem wystąpienia zdarzenia w grupie kontrolnej.

Oblicza się go w następujący sposób:

• Ryzyko względne = [A/(A+B)] / [C/(C+D)]

Następnie możemy użyć poniższego wzoru do obliczenia przedziału ufności dla ryzyka względnego (RR):

• CI mniejszy niż 95% = e ^{ln(RR) – 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}
• CI większy niż 95% = e ^{ln(RR) + 1,96√ 1/a + 1/c – 1/(a+b) – 1/(c+d)}

Poniższy przykład pokazuje, jak w praktyce obliczyć ryzyko względne i odpowiadający mu przedział ufności.

Przykład: Obliczanie przedziału ufności dla ryzyka względnego

Załóżmy, że trener koszykówki stosuje nowy program szkoleniowy, aby sprawdzić, czy zwiększa on liczbę zawodników, którzy mogą przejść określony test umiejętności, w porównaniu ze starym programem szkoleniowym.

Do korzystania z każdego programu trener rekrutuje 50 zawodników. Poniższa tabela przedstawia liczbę graczy, którzy przeszli i nie przeszli testu umiejętności, w zależności od programu, z którego korzystali:

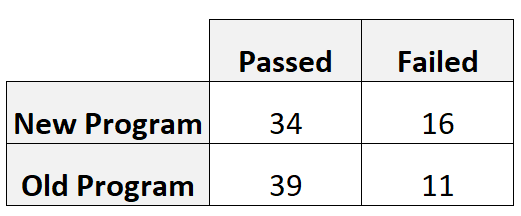
Ryzyko względne możemy obliczyć w następujący sposób:

• Ryzyko względne = [A/(A+B)] / [C/(C+D)]
• Ryzyko względne = [34/(34+16)] / [39/(39+11)]
• Ryzyko względne = 0,8718

Interpretujemy to w ten sposób, że prawdopodobieństwo, że gracz zda test przy użyciu nowego programu, jest tylko 0,8718 razy większe od prawdopodobieństwa, że gracz zda test przy użyciu starego programu.

Innymi słowy, dzięki zastosowaniu nowego programu prawdopodobieństwo zdania testu przez gracza jest faktycznie zmniejszone.

Następnie możemy użyć następujących wzorów do obliczenia 95% przedziału ufności dla ryzyka względnego:

• CI mniejszy niż 95% = e ^{ln(0,8718) – 1,96√ (1/34 + 1/39 – 1/(34+16) – 1/(39+11)} = 0,686
• CI większy niż 95% = e ^{ln(0,8718) + 1,96√ (1/34 + 1/39 + 1/(34+16) – 1/(39+11)} = 1,109

Zatem 95% przedział ufności dla ryzyka względnego wynosi [0,686; 1,109] .

Mamy 95% pewności, że prawdziwe ryzyko względne pomiędzy nowym i starym programem szkoleniowym mieści się w tym przedziale.

Ponieważ ten przedział ufności zawiera wartość 1, nie jest on istotny statystycznie.

Powinno to mieć sens, jeśli weźmie się pod uwagę następujące kwestie:

• Ryzyko względne większe niż 1 oznaczałoby, że prawdopodobieństwo, że zawodnik zda test przy użyciu nowego programu, jest większe niż prawdopodobieństwo, że zawodnik zda test przy użyciu starego programu.
• Ryzyko względne mniejsze niż 1 oznaczałoby, że prawdopodobieństwo, że zawodnik zda test przy użyciu nowego programu, jest mniejsze niż prawdopodobieństwo, że zawodnik zda test przy użyciu starego programu.

Zatem, ponieważ nasz 95% przedział ufności dla ryzyka względnego zawiera wartość 1, oznacza to, że prawdopodobieństwo zdania testu umiejętności przez gracza przy użyciu nowego programu może być, ale nie musi, większe niż prawdopodobieństwo, że ten sam gracz przejdzie test przy użyciu nowego programu. nowy program. stary program.

Dodatkowe zasoby

Poniższe samouczki dostarczają dodatkowych informacji na temat ilorazów szans i ryzyka względnego:

Jak interpretować iloraz szans
Jak interpretować ryzyko względne
Jak obliczyć iloraz szans i ryzyko względne w programie Excel