Hipoteza stałej wariancji: definicja i przykład

Regresja liniowa to technika, której używamy do ilościowego określenia związku między jedną lub większą liczbą zmiennych predykcyjnych azmienną odpowiedzi .

Jednym z kluczowych założeń regresji liniowej jest to, że reszty mają stałą wariancję na każdym poziomie zmiennych predykcyjnych.

Jeżeli to założenie nie zostanie zweryfikowane, reszty będą cierpieć z powodu heteroskedastyczności . Kiedy tak się dzieje, szacunki współczynników modelu stają się niewiarygodne.

Jak oceniać stałą wariancję

Najczęstszym sposobem ustalenia, czy reszty modelu regresji mają stałą wariancję, jest utworzenie wykresu dopasowanych wartości względem reszt .

Jest to rodzaj wykresu, który wyświetla dopasowane wartości modelu regresji wzdłuż osi x i reszty tych wartości dopasowane wzdłuż osi y.

Jeśli rozkład reszt jest w przybliżeniu równy na każdym poziomie dopasowanych wartości, mówimy, że założenie o stałej wariancji jest spełnione.

W przeciwnym razie, jeśli rozproszenie reszt systematycznie rośnie lub maleje, założenie to prawdopodobnie zostanie naruszone.

Uwaga : Ten typ wykresu można utworzyć dopiero po dopasowaniu modelu regresji do zbioru danych.

Poniższy wykres przedstawia przykład wykresu dopasowanych wartości w funkcji reszt, który wykazuje stałą wariancję :

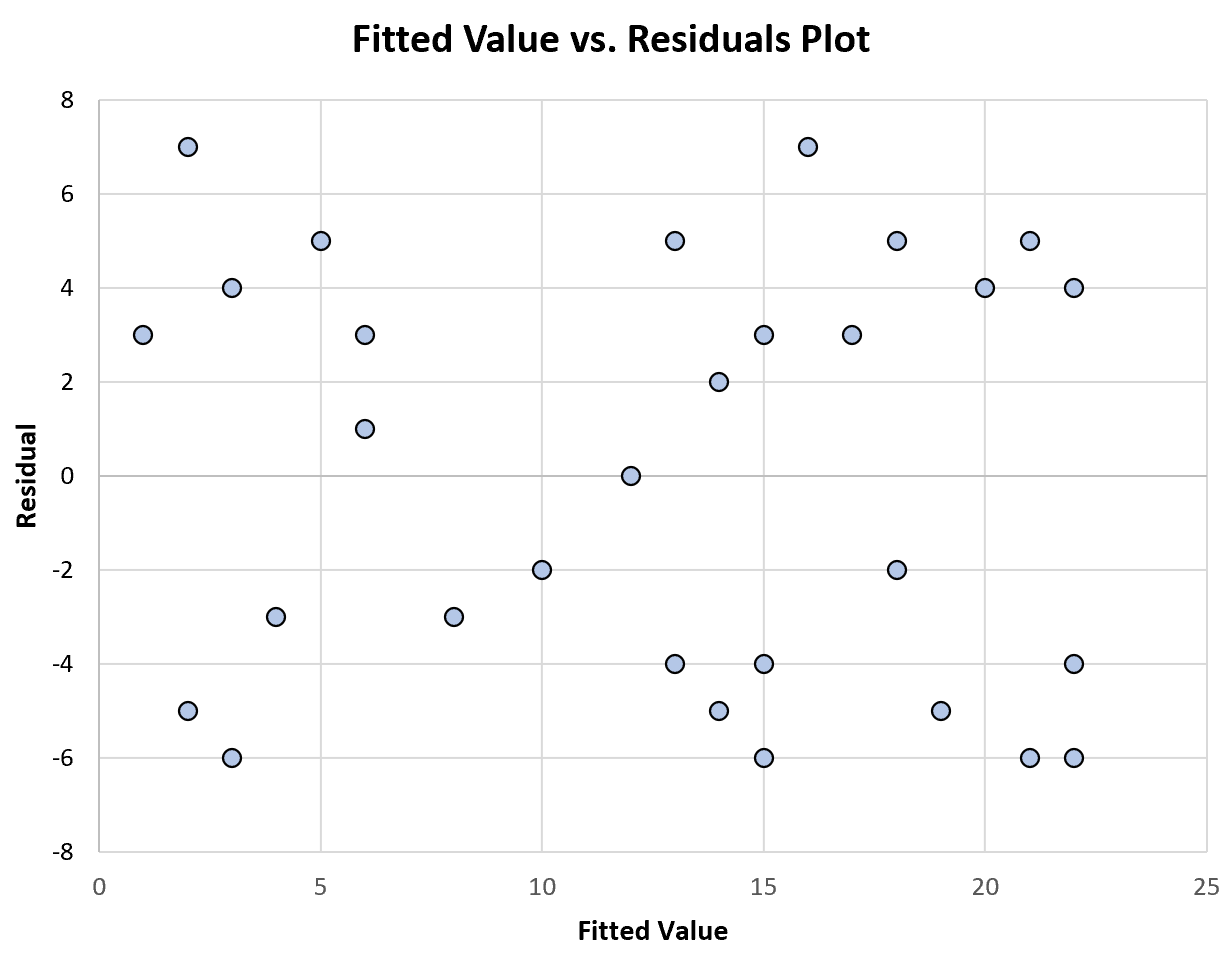
Zwróć uwagę, jak reszty są losowo rozproszone wokół zera, bez określonego wzoru, z w przybliżeniu stałą wariancją na każdym poziomie dopasowanych wartości.

Poniższy wykres przedstawia przykład wykresu dopasowanych wartości w funkcji reszt, który wykazuje niestałą wariancję :

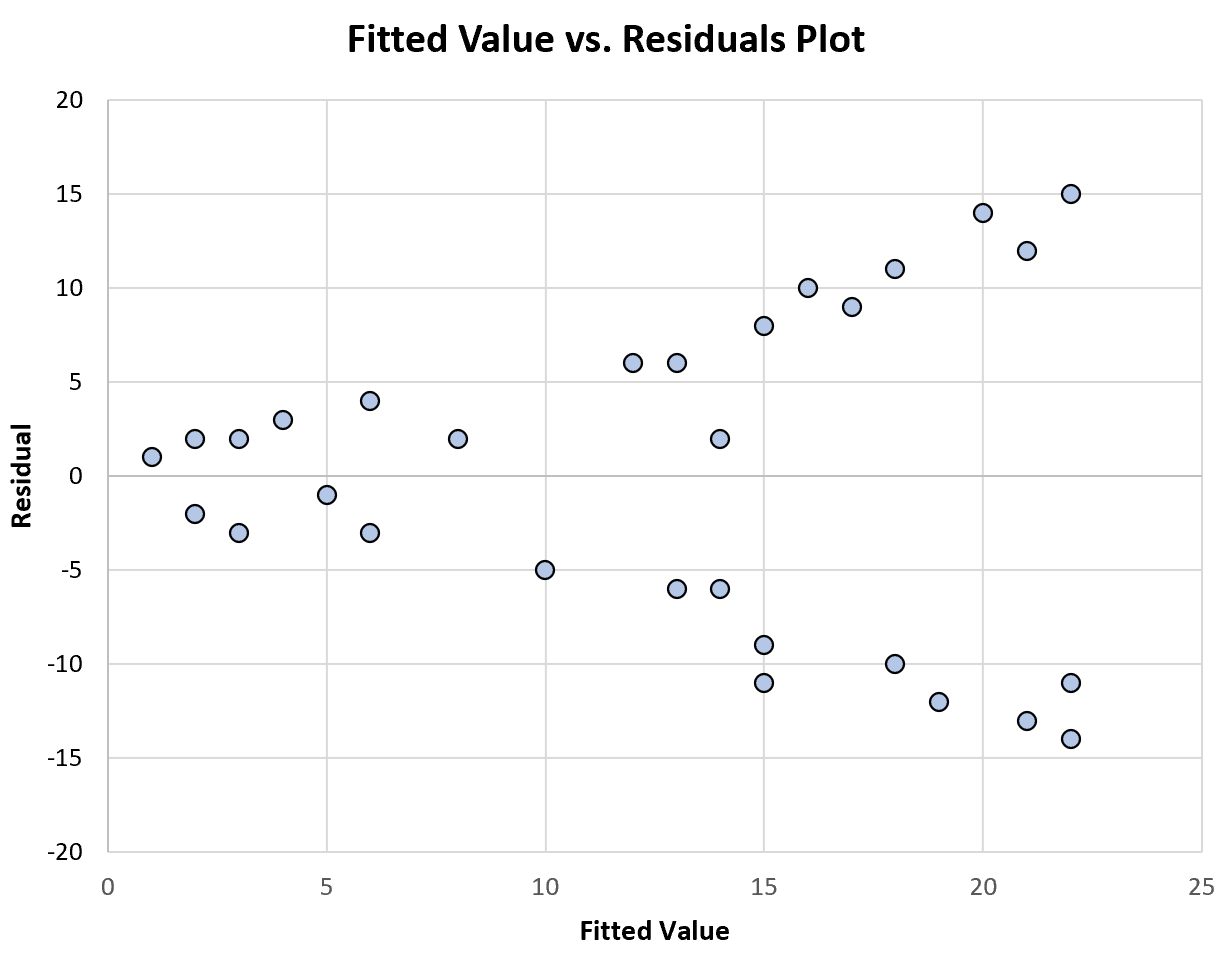
Należy zauważyć, że rozkład reszt staje się większy wraz ze wzrostem dopasowanych wartości. Jest to typowy znak niestałej wariancji.

To mówi nam, że w naszym modelu regresji występuje niestała wariancja reszt, w związku z czym oszacowania współczynników modelu są niewiarygodne.

Jak naprawić naruszenie stałego odchylenia

Jeżeli naruszone zostanie założenie o stałej wariancji, najczęstszym sposobem rozwiązania tego problemu jest przekształcenie zmiennej odpowiedzi za pomocą jednej z trzech transformacji:

1. Transformacja logu: Przekształć zmienną odpowiedzi z y na log(y)

2. Transformacja pierwiastkowa: przekształć zmienną odpowiedzi z y na √y

3. Transformacja pierwiastka sześciennego: przekształć zmienną odpowiedzi z y na y ^1/3

Wykonując te transformacje, problem niestałej wariancji generalnie znika.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat regresji liniowej i analizy reszt:

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Cztery założenia regresji liniowej
Czym są reszty w statystyce?