Jak wykonać anova przy nierównych rozmiarach próbek

Pytanie, które uczniowie często zadają, jeśli chodzi o statystyki, brzmi:

Czy możliwe jest wykonanie jednoczynnikowej analizy ANOVA, gdy wielkość próbek w każdej grupie nie jest równa?

Krótka odpowiedź:

Tak, można przeprowadzić jednoczynnikową ANOVA, gdy rozmiary próbek nie są równe. Równe wielkości próbek nie są jednym z założeń przyjętych w ANOVA.

Istnieją jednak dwie potencjalne kwestie, które należy wziąć pod uwagę podczas wykonywania jednoczynnikowej analizy ANOVA z próbkami o różnej wielkości:

(1) Zmniejszona moc statystyczna.

(2) Solidność zredukowana do nierównej wariancji.

W poniższych sekcjach szczegółowo opisano te dwa potencjalne problemy.

Problem nr 1: Zmniejszona moc statystyczna

Kiedy do porównywania grup używamy dowolnego rodzaju testu statystycznego, moc statystyczna testu jest najwyższa, gdy każda grupa ma równą wielkość próby.

Przypomnijmy, że moc statystyczna odnosi się do prawdopodobieństwa, że test wykryje efekt, gdy taki faktycznie istnieje.

Można wykazać, że im większe różnice w wielkości próby między grupami, tym niższa moc statystyczna analizy ANOVA.

Właśnie dlatego badacze na ogół chcą równych rozmiarów próbek, aby uzyskać większą moc, a tym samym większe prawdopodobieństwo wykrycia prawdziwych różnic.

Z pewnością możliwe jest wykonanie jednokierunkowej analizy ANOVA przy próbkach o różnej wielkości, należy jednak mieć świadomość, że moc jednokierunkowej analizy ANOVA zostanie zmniejszona.

Problem nr 2: Odporność zredukowana do nierównej wariancji

Jednym z założeń jednokierunkowej analizy wariancji jest to, że wariancja pomiędzy każdą grupą jest równa.

Ogólnie rzecz biorąc, jednoczynnikową ANOVA uważa się za odporną na naruszenia założenia o równych wariancjach, ale tylko wtedy, gdy każda grupa ma tę samą wielkość próby .

Tak więc, jeśli masz nierówną wielkość próbek i nierówne wariancje między grupami, wówczas wyniki jednokierunkowej ANOVA mogą być trudne do zaufania.

Jak zdecydować, czy zastosować jednoczynnikową analizę ANOVA przy nierównych rozmiarach próbek

Jeśli masz nierówną wielkość próbek i chcesz przeprowadzić jednoczynnikową analizę ANOVA, aby sprawdzić różnice między średnimi grupowymi, możesz skorzystać z poniższego schematu blokowego, aby zdecydować, jak postępować:

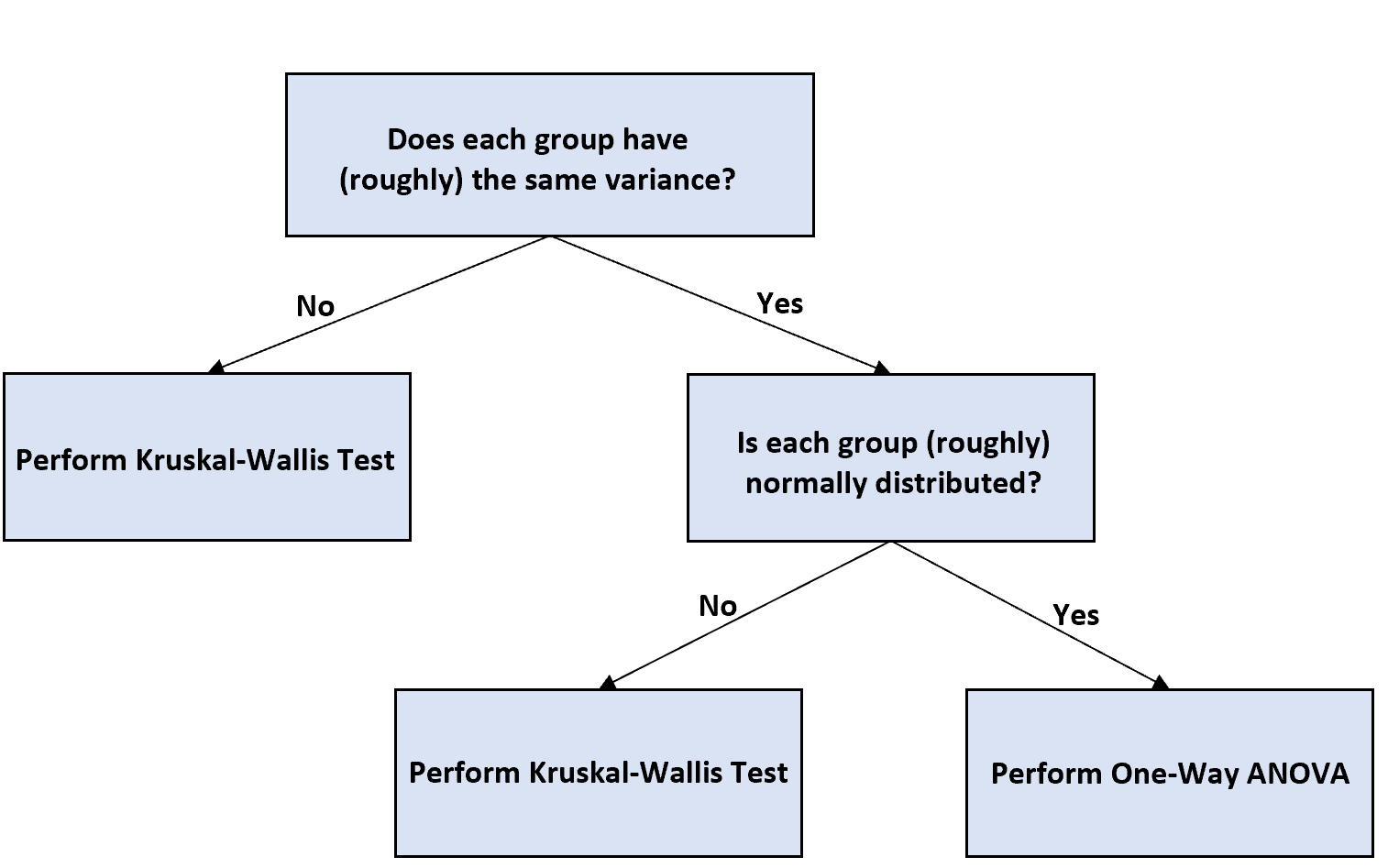
Oto krótkie wyjaśnienie schematu blokowego:

Krok 1: Ustal, czy każda grupa ma tę samą wariancję.

Aby określić, czy każda grupa ma tę samą wariancję, można zastosować jedno z dwóch podejść:

• Utwórz wykresy skrzynkowe dla każdej grupy i sprawdź, czy rozkład wartości w każdej grupie jest w przybliżeniu równy.
• Wykonaj formalny test statystyczny dla równych wariancji, taki jak test Bartletta .

Jeśli wariancje nie są równe, wykonaj test Kruskala-Wallisa , który jest uważany za nieparametryczny odpowiednik jednoczynnikowej analizy ANOVA.

Jeśli odstępy są równe, przejdź do następnego kroku.

Krok 2: Określ, czy każda grupa ma rozkład normalny.

Aby ustalić, czy wartości w każdej grupie mają w przybliżeniu rozkład normalny, możesz zastosować jedno z dwóch podejść:

• Utwórz histogramy lub wykresy QQ dla każdej grupy.
• Wykonuj formalne testy statystyczne, takie jak Shapiro-Wilk, Kołmogorow-Smironow, Jarque-Barre lub D’Agostino-Pearson.

Jeśli każda grupa ma rozkład normalny, można przeprowadzić jednokierunkową analizę ANOVA i zinterpretować wyniki w taki sam sposób, jak każdą zwykłą jednokierunkową analizę ANOVA.

Jeśli każda grupa nie ma rozkładu normalnego, wykonaj zamiast tego test Kruskala-Wallisa.

Dodatkowe zasoby

Wprowadzenie do jednokierunkowej ANOVA
Jak sprawdzić założenia ANOVA
Wprowadzenie do testu Kruskala-Wallisa
Jak interpretować wartość F i wartość P w ANOVA