Standardowy rozkład normalny

W tym artykule wyjaśniono, czym jest standardowy rozkład normalny i do czego się go używa. Znajdziesz tu także właściwości standardowego rozkładu normalnego, tabelę z jego charakterystycznymi wartościami oraz dodatkowo rozwiązane ćwiczenie.

Jaki jest standardowy rozkład normalny?

Standardowy rozkład normalny , zwany także jednostkowym rozkładem normalnym , jest najprostszym przypadkiem rozkładu normalnego. Dokładniej, standardowy rozkład normalny jest rozkładem normalnym o wartościach średniej i odchylenia standardowego równych odpowiednio 0 i 1.

Dlatego standardowy rozkład normalny definiuje się jako N(0,1), gdzie pierwszy parametr jest średnią rozkładu, a drugi parametr jest jego odchyleniem standardowym (lub SD).

Wykres standardowego rozkładu normalnego wygląda zatem następująco:

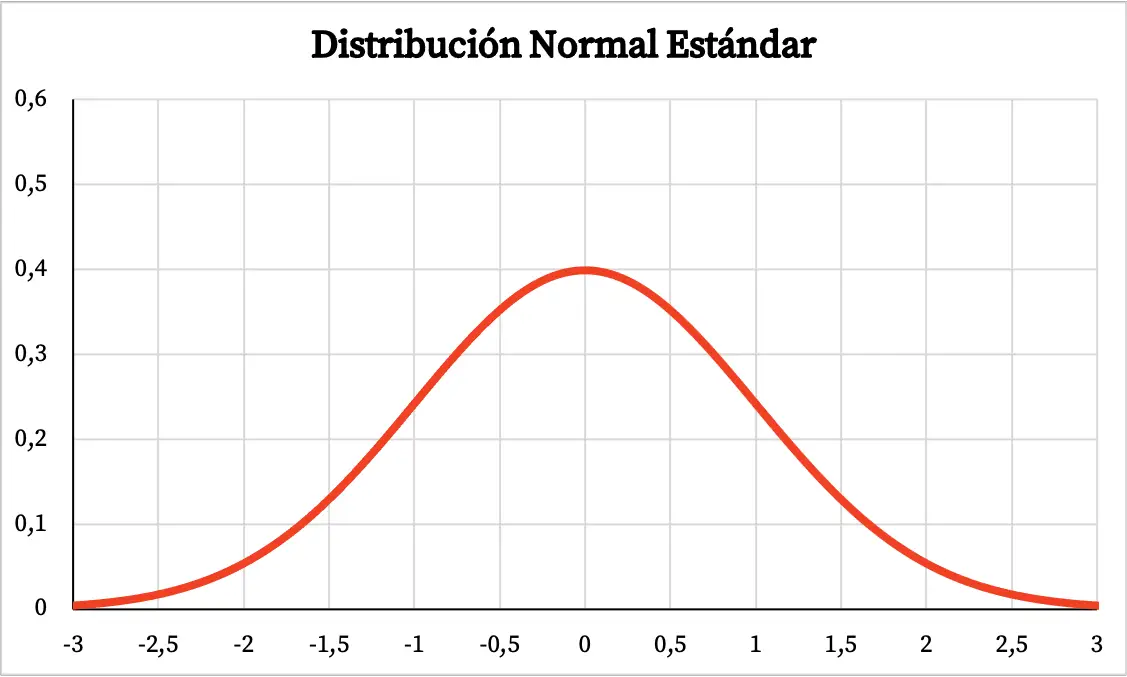
Wzór na standardowy rozkład normalny

Aby przekształcić dowolny rozkład normalny w standardowy rozkład normalny, należy od wszystkich jego wartości odjąć średnią rozkładu normalnego, a następnie podzielić przez odchylenie standardowe rozkładu normalnego.

Wzór na standardowy rozkład normalny jest zatem następujący:

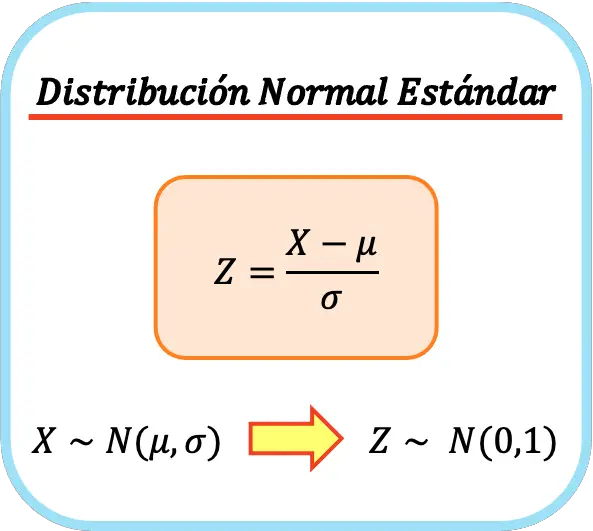
W ten sposób średnia arytmetyczna i odchylenie standardowe nowej zmiennej wyniosą odpowiednio 0 i 1, a więc otrzymamy standardowy rozkład normalny. Proces ten nazywany jest także normalizacją jednowymiarową lub normalizacją jednowymiarową .

Standardowa tabela rozkładu normalnego

Tablica standardowego rozkładu normalnego to tabela zawierająca prawdopodobieństwa, że zaobserwowana wartość jest mniejsza niż dana wartość standardowego rozkładu normalnego.

Ponadto, ponieważ funkcja rozkładu normalnego zależy od jego średniej i odchylenia standardowego, tabela standardowego rozkładu normalnego jest również wykorzystywana w rozszerzeniu do określania prawdopodobieństw dowolnego rozkładu normalnego. Aby to zrobić, rozkład normalny wpisuje się do standardowego rozkładu normalnego, a następnie sprawdzamy w tabeli, jakie prawdopodobieństwo mu odpowiada.

Zatem wartości w standardowej tabeli rozkładu normalnego są następujące:

Przykład standardowego rozkładu normalnego

Teraz, gdy znamy już definicję standardowego rozkładu normalnego i jego wzór, poniżej znajduje się konkretny przykład pozwalający dobrze zrozumieć tę koncepcję.

• Ciągła zmienna losowa ma rozkład normalny ze średnią 45 i odchyleniem standardowym 15. Jakie jest prawdopodobieństwo otrzymania wartości mniejszej lub równej 58?

Aby znaleźć prawdopodobieństwo rozkładu normalnego, musimy skorzystać z jego tabeli cech, ale w tym celu musimy najpierw wykonać proces wpisywania, aby uzyskać standardowy rozkład normalny. Dlatego używamy standardowego wzoru na rozkład normalny:

Odejmujemy więc średnią od wartości prawdopodobieństwa i dzielimy przez odchylenie standardowe

Po standaryzacji zmiennej przechodzimy do standardowej tabeli prawdopodobieństwa rozkładu normalnego (patrz wyżej), aby sprawdzić, jakiemu prawdopodobieństwu odpowiada wartość 0,87:

Prawdopodobieństwo uzyskania wartości równej lub mniejszej od 58 wynosi zatem 80,78%.

Charakterystyka standardowego rozkładu normalnego

Standardowy rozkład normalny ma następujące cechy:

• Standardowy rozkład normalny to rozkład symetryczny ze środkiem na 0.
• Podobnie jak rozkład normalny, standardowy wykres rozkładu normalnego ma kształt dzwonu, a większość obszaru wykresu mieści się wokół średniej.
• Dlatego średnia, tryb i mediana rozkładu normalnego mają tę samą wartość, czyli 0.
• Standardowy rozkład normalny ma maksimum przy z=0.
• Podobnie standardowy rozkład normalny ma dwa punkty przegięcia, przy z=-1 i z=+1.
• Zgodnie z praktyczną zasadą wiemy, że 68% wartości mieści się w standardowym rozkładzie normalnym pomiędzy +1 a -1, 95% wartości pomiędzy +2 a -2 i 99,7% wartości pomiędzy + 3 i – 3.