Interpolacja czy ekstrapolacja: jaka jest różnica?

Dwa terminy, które uczniowie często mylą w statystyce, to interpolacja i ekstrapolacja .

Oto różnica:

Interpolacja odnosi się do przewidywania wartości mieszczących się w zakresie punktów danych.

Ekstrapolacja odnosi się do przewidywania wartości wykraczających poza zakres punktów danych.

Poniższy przykład ilustruje różnicę między tymi dwoma terminami.

Przykład: interpolacja i ekstrapolacja

Załóżmy, że mamy następujący zbiór danych:

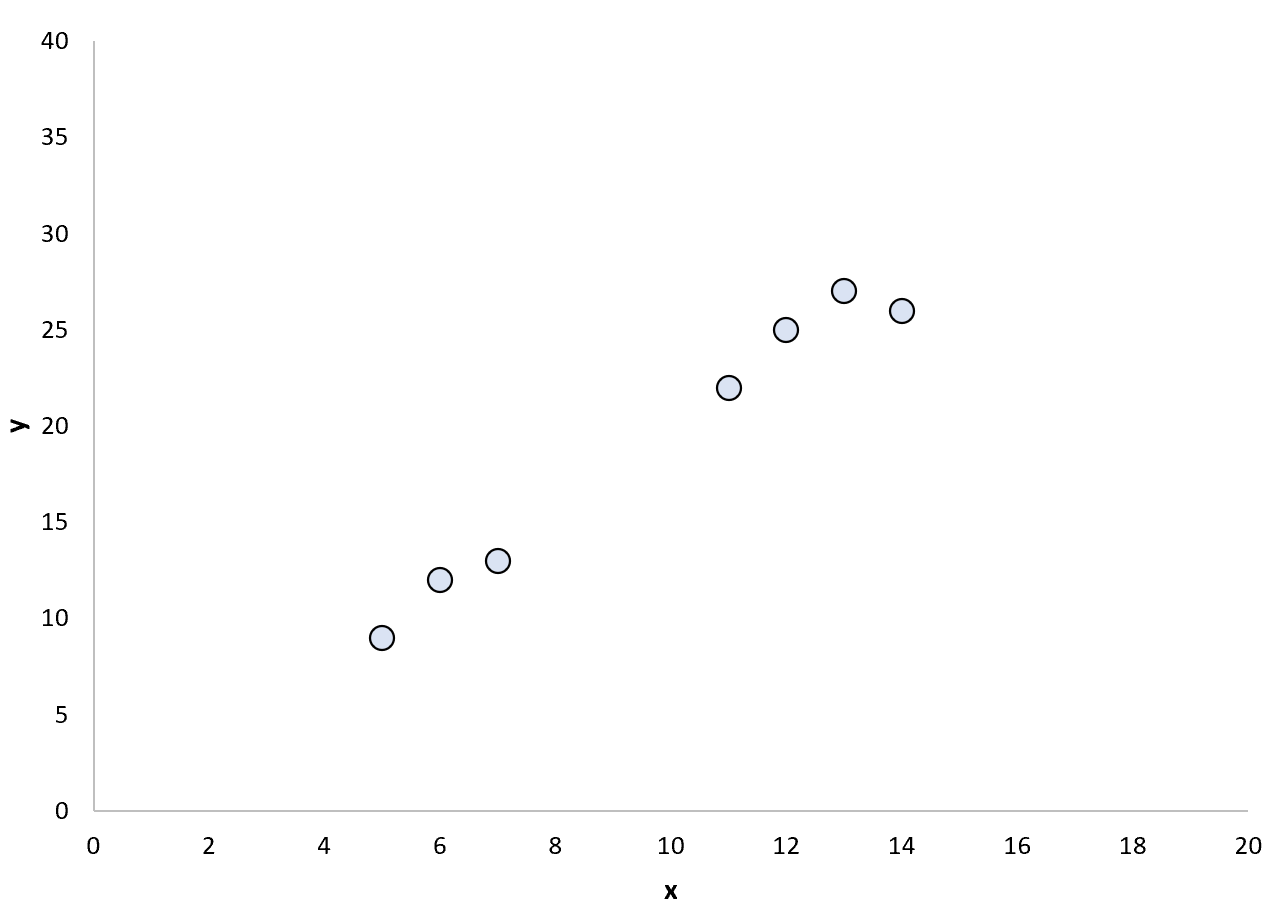
Możemy zdecydować się na dopasowanie prostego modelu regresji liniowej do tych punktów:

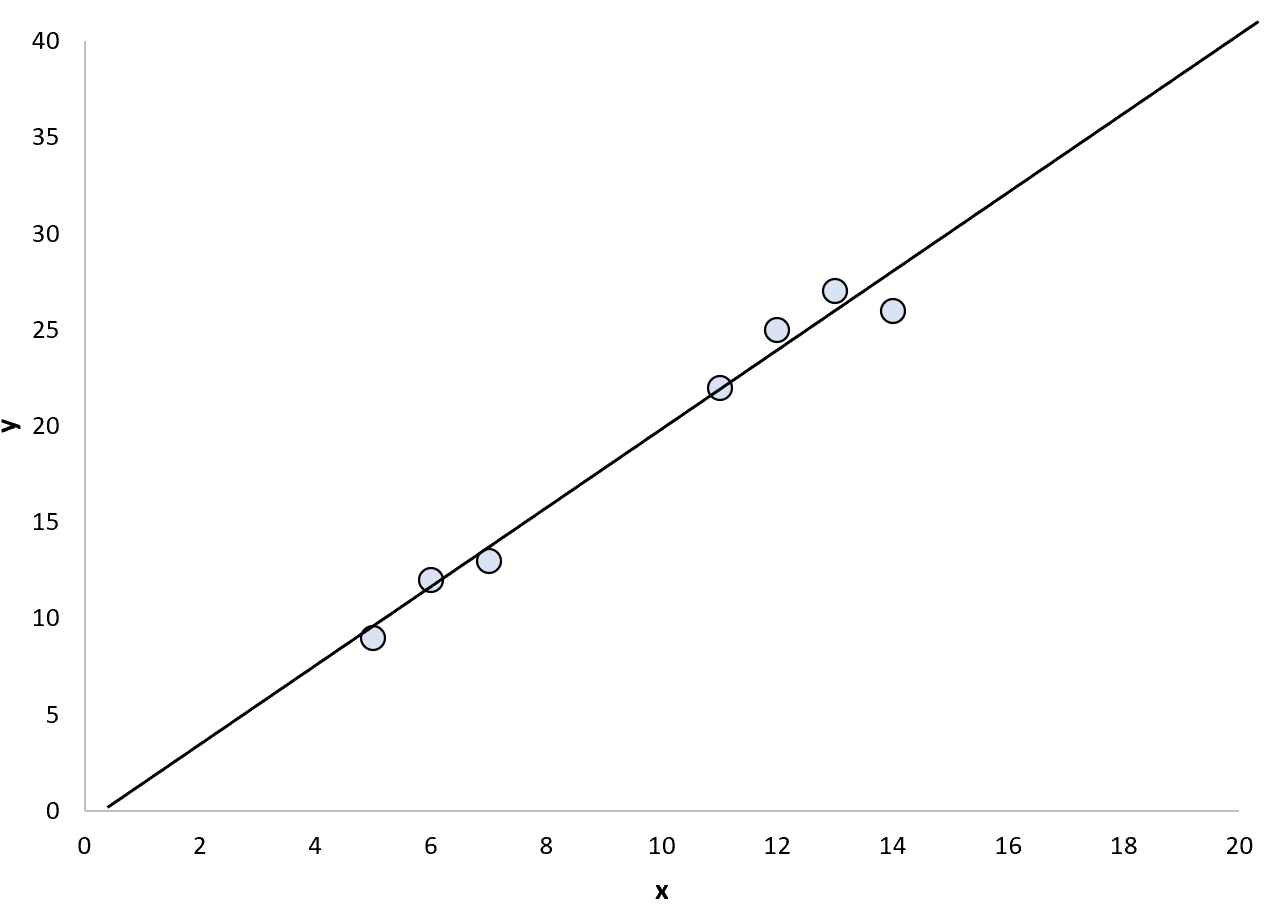
Moglibyśmy następnie użyć dopasowanego modelu regresji do przewidywania wartości punktowych zarówno wewnątrz , jak i na zewnątrz zakresu punktów danych.

Kiedy używamy dopasowanego modelu regresji do przewidywania wartości punktowych w istniejącym zakresie punktów danych, nazywa się to interpolacją.

I odwrotnie, gdy używamy dopasowanego modelu regresji do przewidywania wartości punktowych poza istniejącym zakresem, nazywa się to ekstrapolacją :

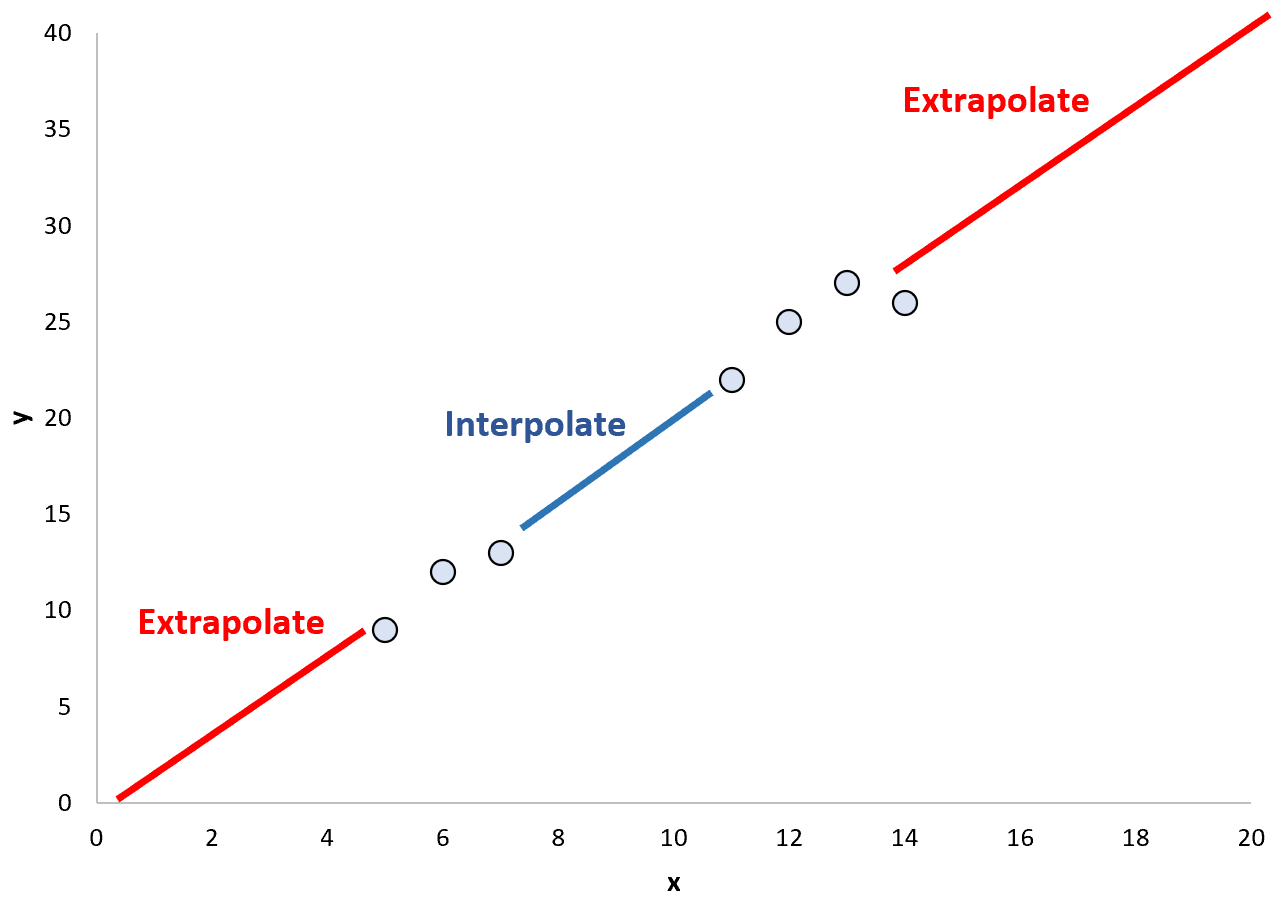
Potencjalne niebezpieczeństwo ekstrapolacji

Dokonując ekstrapolacji, zakładamy, że ten sam wzorzec, który istnieje w bieżącym zakresie punktów danych, istnieje również poza tym zakresem.

Może to być jednak niebezpieczne założenie, ponieważ możliwe jest, że wzorzec istniejący poza bieżącym zakresem punktów danych jest bardzo różny:

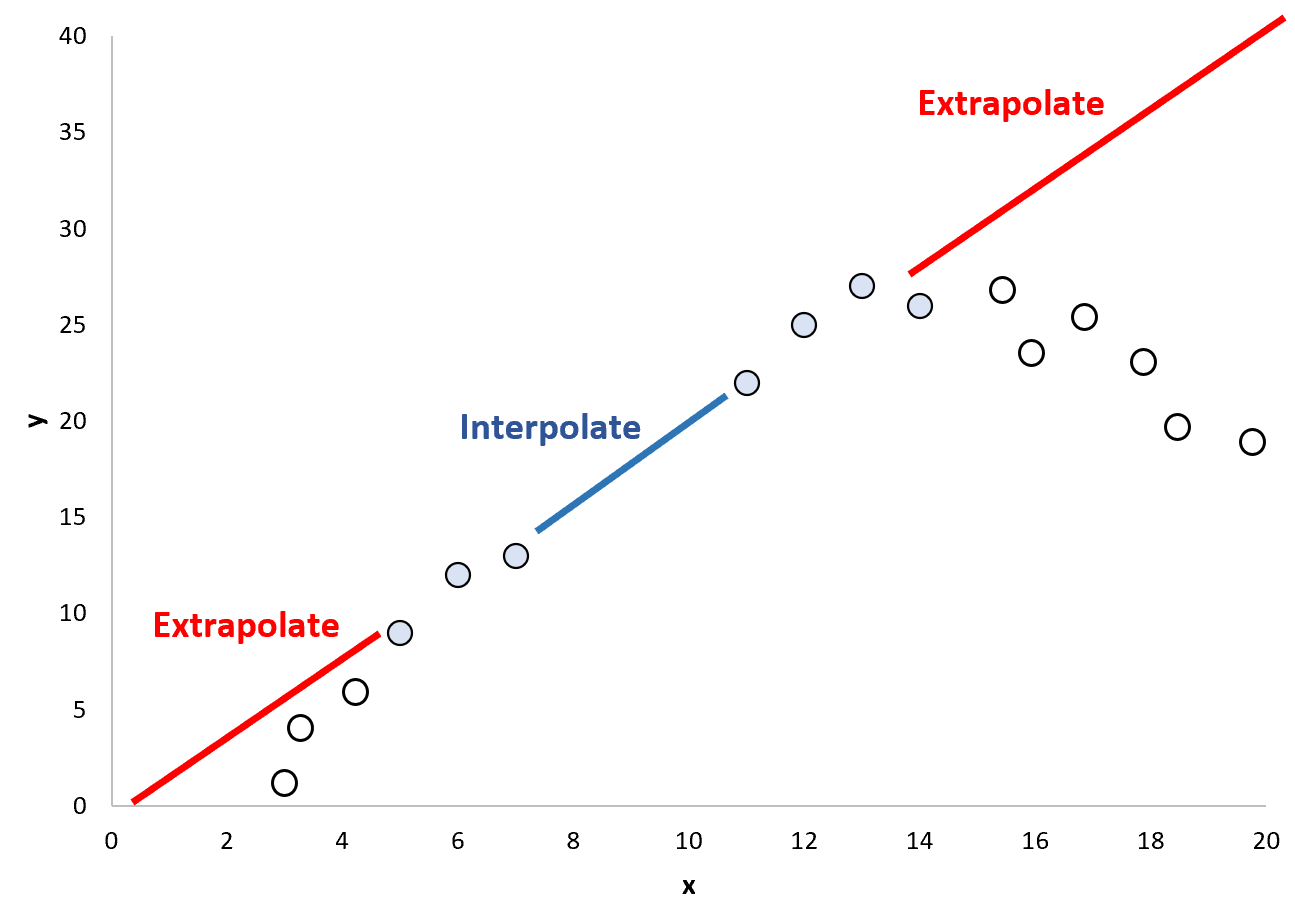
Z tego powodu stosowanie ekstrapolacji do przewidywania wartości punktów danych, które wykraczają poza zakres wartości użytych do utworzenia modelu regresji, może być niebezpieczne.

W praktyce często ma sens zastosowanie ekstrapolacji do przewidywania wartości punktowych, które nieznacznie wykraczają poza zakres istniejących wartości, jednak im dalej od tego zakresu się oddalamy, tym większe jest prawdopodobieństwo, że różnica pomiędzy wartością przewidywaną a rzeczywistą wartość jest ważna. .

Kiedy stosować ekstrapolację

Często potrzeba specjalistycznej wiedzy specjalistycznej w danej dziedzinie, aby określić, czy ekstrapolacja jest rozsądnym pomysłem, czy nie.

Załóżmy na przykład, że dział marketingu firmy stosuje prosty model regresji liniowej, wykorzystując wydatki na reklamę jako zmienną predykcyjną i całkowite przychody jako zmienną odpowiedzi.

W tym scenariuszu rozsądne może być założenie, że stały wzrost wydatków na reklamę spowoduje przewidywalny wzrost całkowitych przychodów:

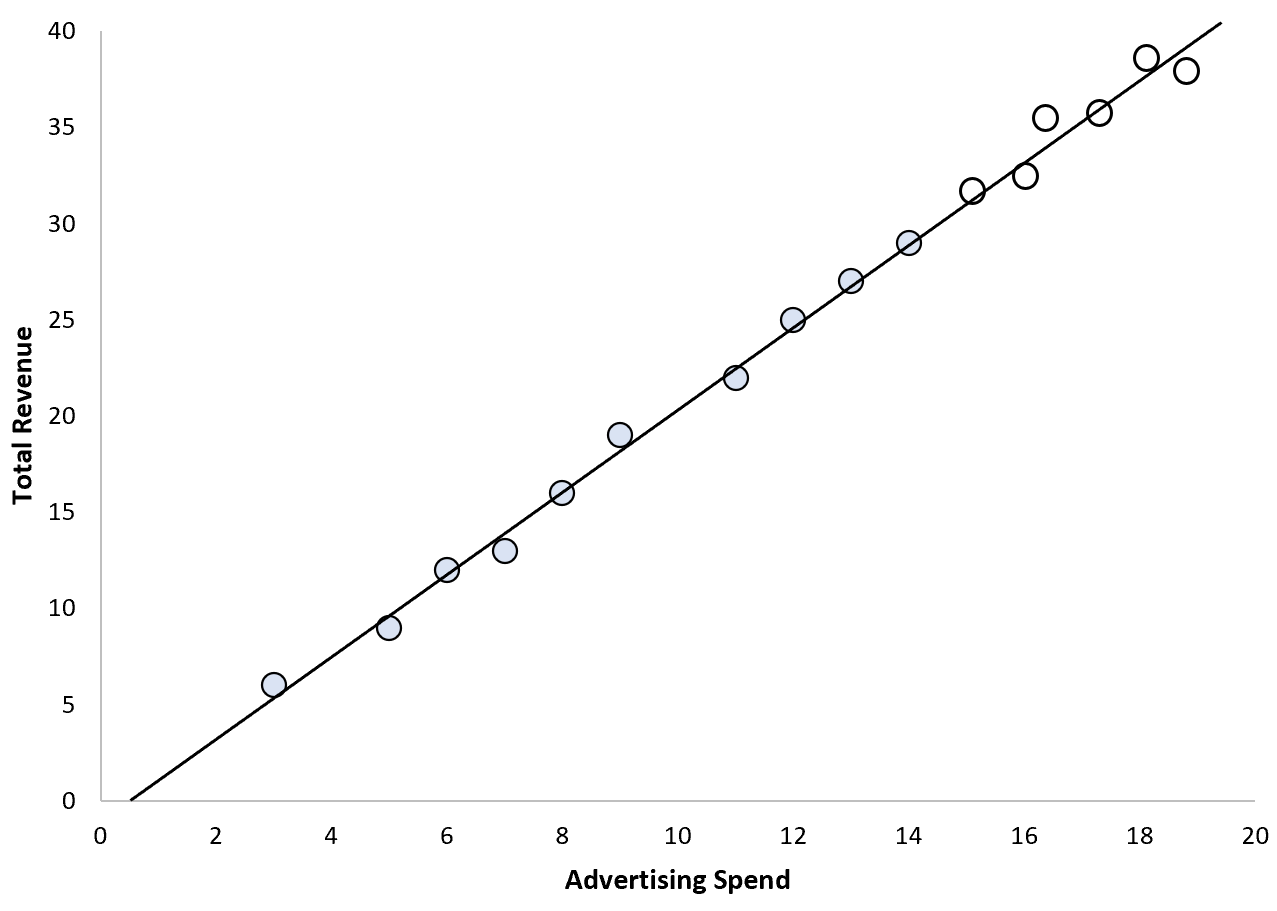
W tym scenariuszu możemy być całkiem pewni naszej zdolności do ekstrapolacji wartości.

Rozważmy jednak scenariusz, w którym biolog chce zastosować nawóz całkowity do przewidywania wzrostu roślin.

Może zdecydować się na dopasowanie prostego modelu regresji liniowej do punktów danych, ale ponieważ istnieje górna granica wysokości rośliny, prawdopodobnie nie ma sensu stosowanie ekstrapolacji do przewidywania wartości punktów. poza zakresem wartości. wartości użyte do dopasowania modelu:

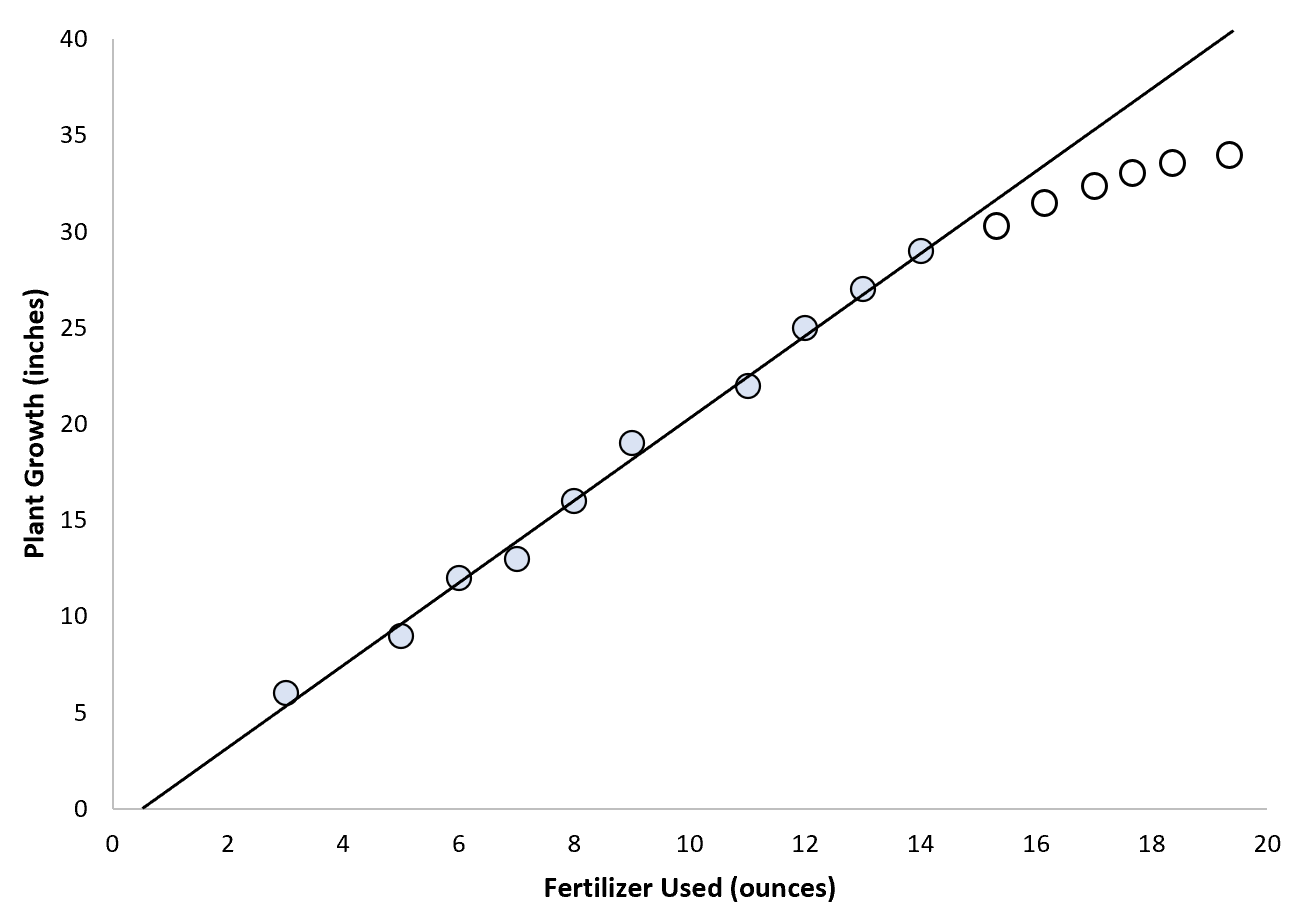
W tym scenariuszu możemy mieć znacznie mniejszą pewność co do naszej zdolności do ekstrapolacji wartości.

Wniosek na wynos : Ekstrapolacja może mieć większy sens w niektórych obszarach niż w innych, ale zawsze istnieje potencjalne niebezpieczeństwo, że model, który istnieje w zakresie wartości zastosowanych do dopasowania modelu, nie istnieje poza plażą.

Dodatkowe zasoby

Jak wykonać interpolację liniową w programie Excel
Jak dokonywać prognoz za pomocą regresji liniowej