Rozkład gamma

Przez Benjamin Anderson 3 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład gamma i do czego się go używa. W ten sposób znajdziesz definicję rozkładu gamma, jego właściwości i jak wygląda jego graficzna reprezentacja.

Jaki jest rozkład gamma?

Rozkład gamma jest ciągłym rozkładem prawdopodobieństwa zdefiniowanym przez dwa charakterystyczne parametry, α i λ. Inaczej mówiąc, rozkład gamma zależy od wartości jego dwóch parametrów: α jest parametrem kształtu, a λ jest parametrem skali.

Symbolem rozkładu gamma jest wielka grecka litera Γ. Zatem, jeśli zmienna losowa ma rozkład gamma, zapisuje się ją w następujący sposób:

$X\sim \Gamma(\alpha,\lambda)$

Rozkład gamma można również parametryzować za pomocą parametru kształtu k = α i parametru odwrotnej skali θ = 1/λ. We wszystkich przypadkach dwa parametry definiujące rozkład gamma są dodatnimi liczbami rzeczywistymi.

Zazwyczaj rozkład gamma jest używany do modelowania zbiorów danych skośnych w prawo, dzięki czemu po lewej stronie wykresu występuje większa koncentracja danych. Na przykład rozkład gamma służy do modelowania niezawodności komponentów elektrycznych.

Schemat rozkładu gamma

Wykres rozkładu gamma zależy od wartości jego charakterystycznych parametrów. Poniżej możesz zobaczyć, jak zmienia się funkcja gęstości rozkładu gamma w zależności od parametru kształtu i parametru skali.

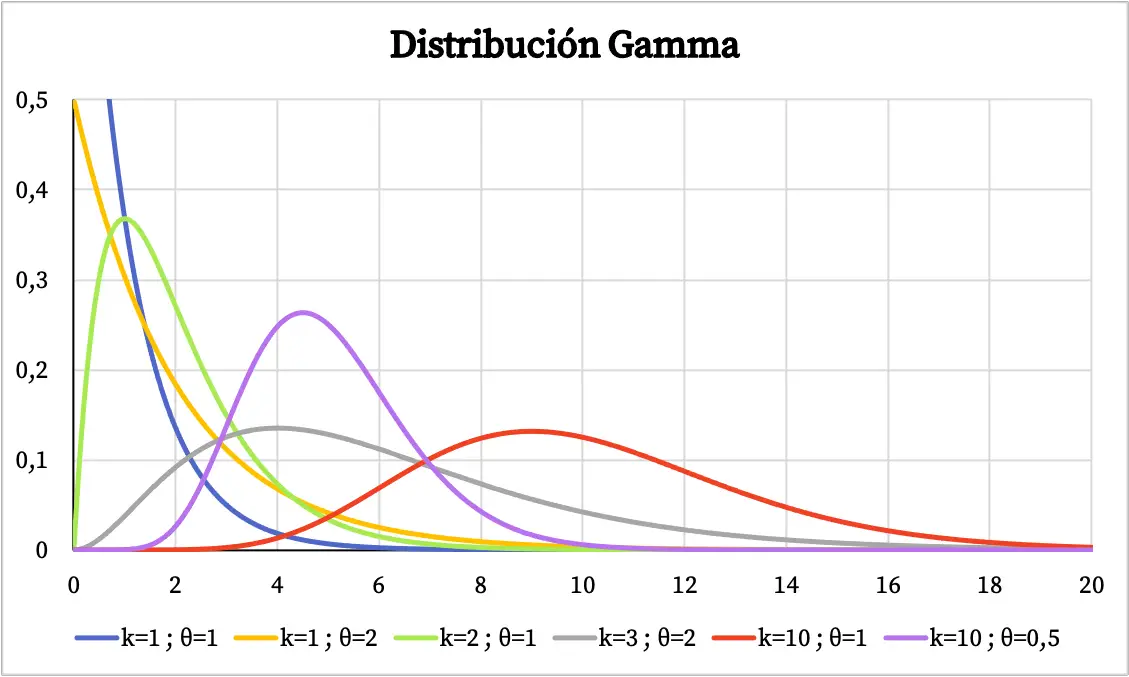
Z drugiej strony, poniżej możesz zobaczyć wykres skumulowanej funkcji prawdopodobieństwa rozkładu gamma:

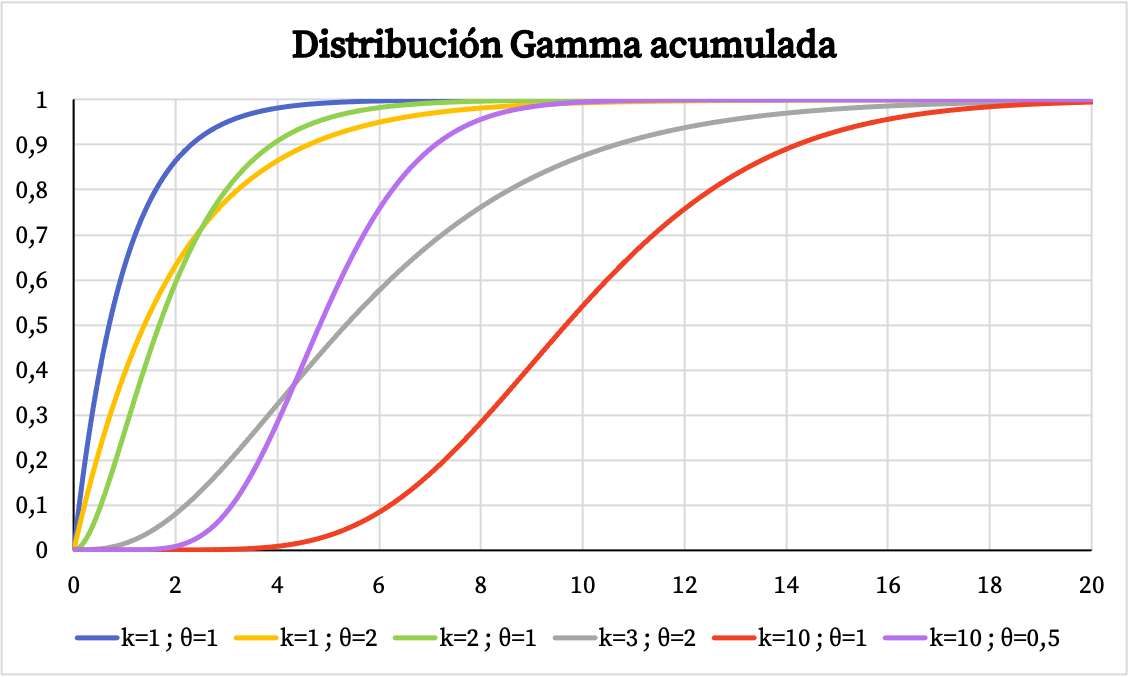
Charakterystyka rozkładu gamma

Zobaczymy wtedy, jakie są cechy rozkładu gamma.

Wykres rozkładu gamma jest całkowicie zdefiniowany przez jego dwa charakterystyczne parametry: α jest parametrem kształtu, a λ jest parametrem skali.

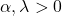
$\alpha , \lambda >0″ title=”Rendered by QuickLaTeX.com” height=”16″ width=”62″ style=”vertical-align: -4px;”></p> </p> <ul> <li> Dziedzina rozkładu gamma składa się wyłącznie z liczb dodatnich.</li> </ul> <p class=$ $x\in (0,+\infty)$

Średnia rozkładu gamma jest równa stosunkowi parametru kształtu do parametru skali, tj. α/λ.

$E[X]=\cfrac{\alpha}{\lambda}$

Wariancja rozkładu gamma jest równa parametrowi kształtu podzielonemu przez kwadrat parametru skali.

$Var(X)=\cfrac{\alpha}{\lambda^2}$

Dla wartości α mniejszych niż 1 tryb wynosi 0. Jeśli jednak α jest równe lub większe niż 1, tryb rozkładu gamma można obliczyć za pomocą następującego wzoru:

$\begin{array}{c}Mo=0 \qquad \text{para } \alpha<1\\[2ex]Mo=\cfrac{\alpha-1}{\lambda} \qquad \text{para } \alpha\geq1\end{array}$

Wzór na funkcję gęstości rozkładu gamma to:

$\displaystyle f(x)=\frac{\lambda(\lambda x)^{\alpha-1}e^{-\lambda x}}{\Gamma(\alpha)}$

Gdzie Γ jest funkcją gamma zdefiniowaną jako:

$\displaystyle \Gamma(\alpha)=\int_0^\infty t^{\alpha-1}e^{-t}dt$

Wzór na skumulowany rozkład zmiennej losowej określonej rozkładem gamma jest następujący:

$\displaystyle F(x)=\int_0^x\frac{\lambda(\lambda y)^{\alpha-1}e^{-\lambda y}}{\Gamma(\alpha)}\;dy$

Jeśli parametr kształtu α jest równy 1, wówczas rozkład gamma jest równoważny rozkładowi wykładniczemu z tym samym parametrem skali λ.

$X\sim \Gamma(1,\lambda) \ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \text{Exp}(\lambda)$

Gdy parametr skali λ jest średnią, wówczas rozkład gamma jest szczególnym przypadkiem rozkładu chi-kwadrat .

$\displaystyle X\sim \Gamma\left(\frac{n}{2},\frac{1}{2}\right) \text{con } n\in \mathbb{N}\ \color{orange}\bm{\longrightarrow}\color{black} \ X\sim \chi_n^2$

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Jaki jest rozkład gamma?

Schemat rozkładu gamma

Charakterystyka rozkładu gamma

o autorze

Dr Benjamin Anderson

Dodaj komentarz