Jak przekształcać dane w pythonie (log, pierwiastek kwadratowy, pierwiastek sześcienny)
Wiele testów statystycznych zakłada, że zbiory danych mają rozkład normalny. Jednak często tak się nie dzieje w praktyce.
Jednym ze sposobów rozwiązania tego problemu jest przekształcenie rozkładu wartości w zbiorze danych za pomocą jednej z trzech transformacji:
1. Transformacja logu: przekształć zmienną odpowiedzi z y na log(y) .
2. Transformacja pierwiastka kwadratowego: Przekształć zmienną odpowiedzi z y na √y .
3. Transformacja pierwiastka sześciennego: przekształć zmienną odpowiedzi z y na y 1/3 .
Wykonując te przekształcenia, zbiór danych ogólnie ma rozkład bardziej normalny.
Poniższe przykłady pokazują, jak wykonać te transformacje w Pythonie.
Zaloguj transformację w Pythonie
Poniższy kod pokazuje, jak przeprowadzić transformację logarytmiczną zmiennej i utworzyć wykresy obok siebie w celu wyświetlenia pierwotnego rozkładu i rozkładu danych przekształconego logarytmicznie:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 4 , b= 15 , size= 300 ) #create log-transformed data data_log = np. log (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Log-Transformed Data ')
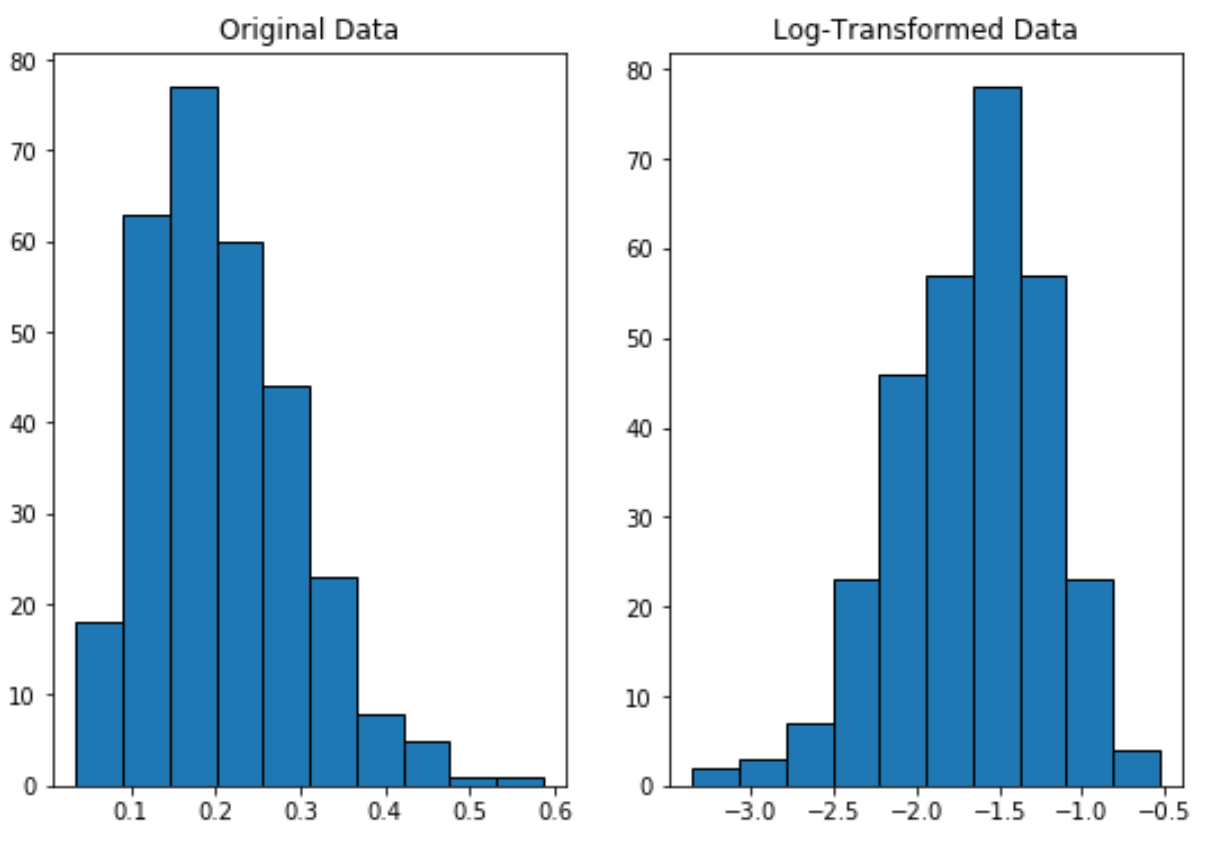
Zwróć uwagę, że rozkład przekształcony logarytmicznie ma rozkład bardziej normalny niż rozkład pierwotny.
Nadal nie jest to idealny „kształt dzwonu”, ale jest bliższy rozkładowi normalnemu niż rozkładowi pierwotnemu.
Transformacja pierwiastkowa w Pythonie
Poniższy kod pokazuje, jak przeprowadzić transformację pierwiastkową zmiennej i utworzyć wykresy obok siebie, aby wyświetlić pierwotny rozkład i rozkład danych przekształcony pierwiastkowo:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. sqrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Square Root Transformed Data ')
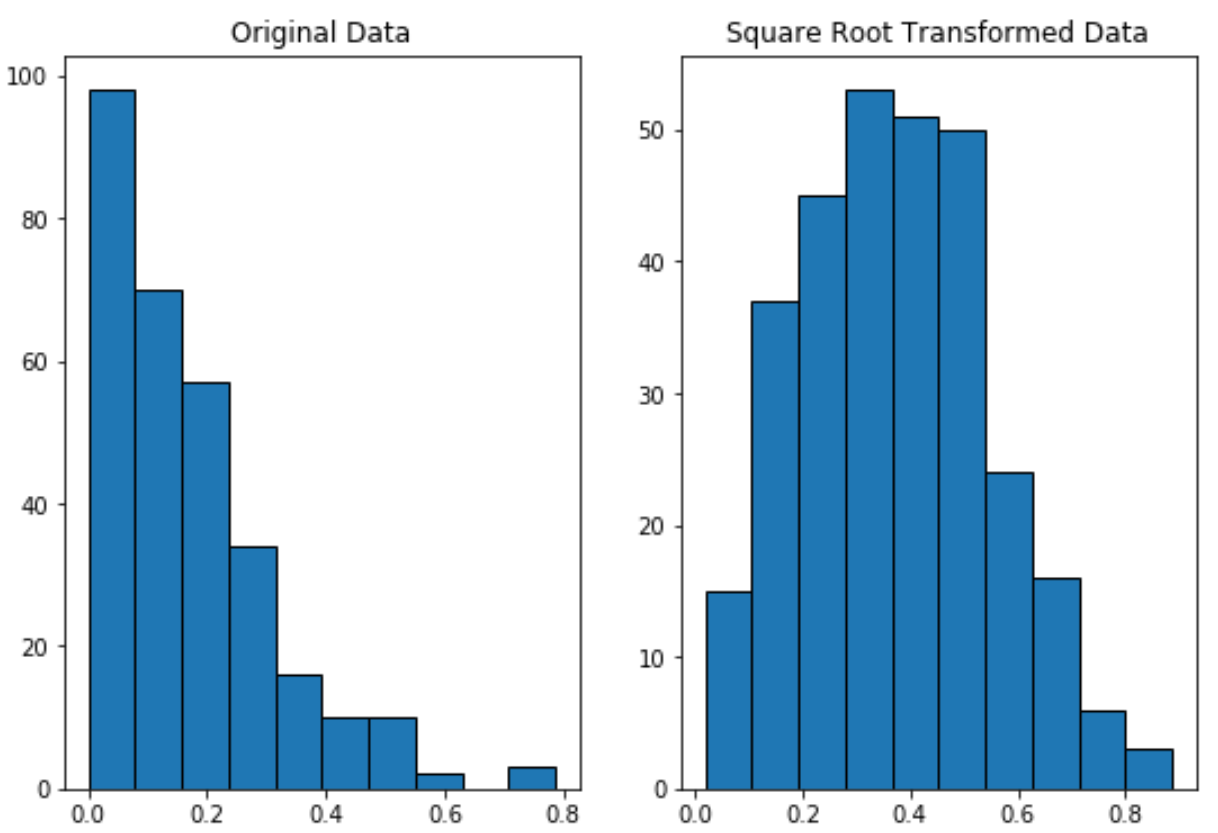
Zwróć uwagę, że dane przekształcone w pierwiastek kwadratowy mają znacznie bardziej normalny rozkład niż dane oryginalne.
Transformacja pierwiastka sześciennego w Pythonie
Poniższy kod pokazuje, jak przeprowadzić transformację pierwiastka sześciennego na zmiennej i utworzyć wykresy obok siebie w celu wyświetlenia pierwotnego rozkładu i rozkładu przekształconego pierwiastka sześciennego danych:
import numpy as np import matplotlib. pyplot as plt #make this example reproducible n.p. random . seeds (0) #create beta distributed random variable with 200 values data = np. random . beta (a= 1 , b= 5 , size= 300 ) #create log-transformed data data_log = np. cbrt (data) #define grid of plots fig, axs = plt. subplots (nrows= 1 , ncols= 2 ) #create histograms axs[0]. hist (data, edgecolor=' black ') axs[1]. hist (data_log, edgecolor=' black ') #add title to each histogram axs[0]. set_title (' Original Data ') axs[1].set_title(' Cube Root Transformed Data ')
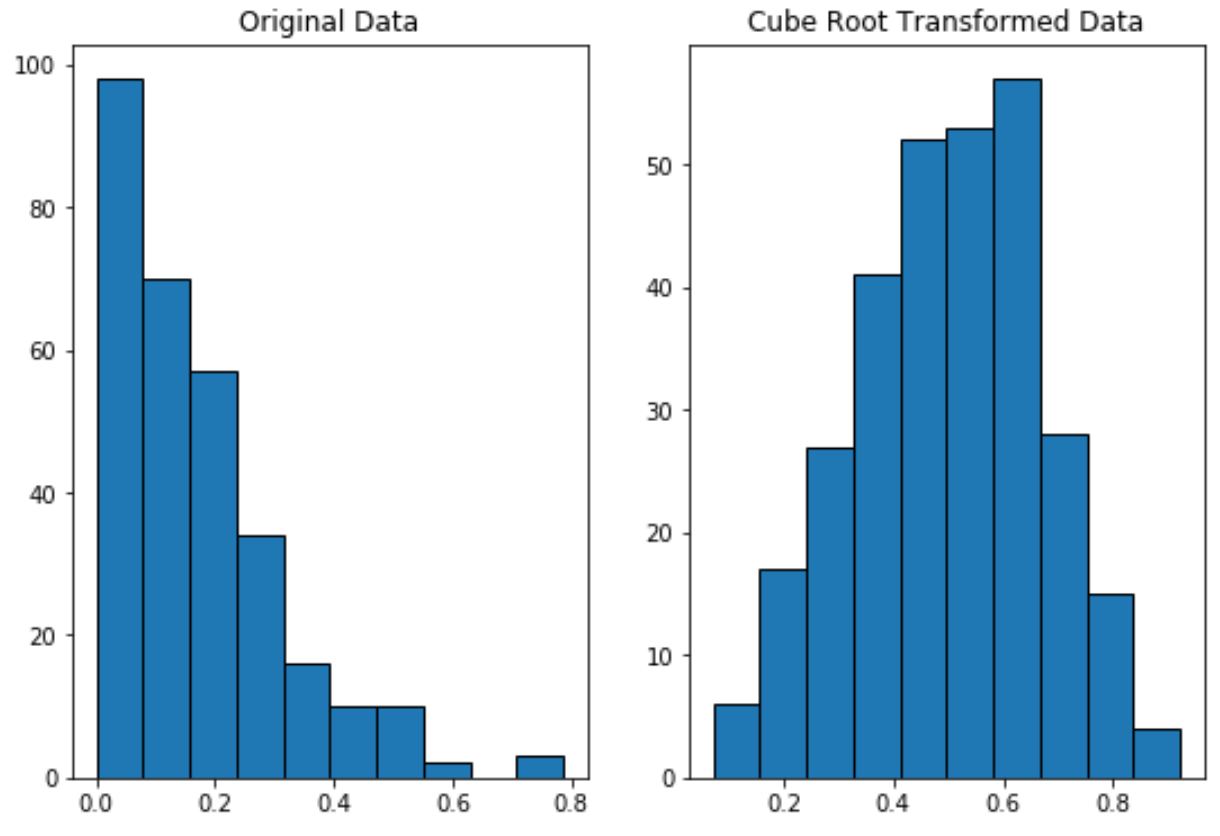
Zwróć uwagę, że dane przekształcone w pierwiastek sześcienny mają znacznie bardziej normalny rozkład niż dane oryginalne.
Dodatkowe zasoby
Jak obliczyć wyniki Z w Pythonie
Jak normalizować dane w Pythonie
Jakie jest założenie normalności w statystyce?