Zrozumienie błędu standardowego nachylenia regresji

Błąd standardowy nachylenia regresji jest sposobem pomiaru „niepewności” w szacowaniu nachylenia regresji.

Oblicza się go w następujący sposób:

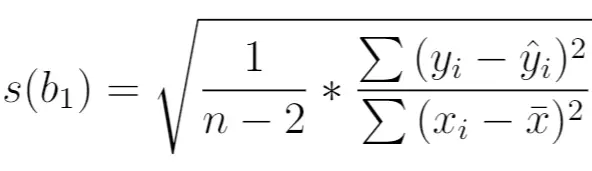
Złoto:

• n : całkowity rozmiar próbki
• y _i : rzeczywista wartość zmiennej odpowiedzi
• ŷ _i : przewidywana wartość zmiennej odpowiedzi
• x _i : rzeczywista wartość zmiennej predykcyjnej
• x̄ : średnia wartość zmiennej predykcyjnej

Im mniejszy błąd standardowy, tym mniejsza zmienność wokół oszacowania współczynnika dla nachylenia regresji.

Błąd standardowy nachylenia regresji będzie wyświetlany w kolumnie „błąd standardowy” w wynikach regresji większości programów statystycznych:

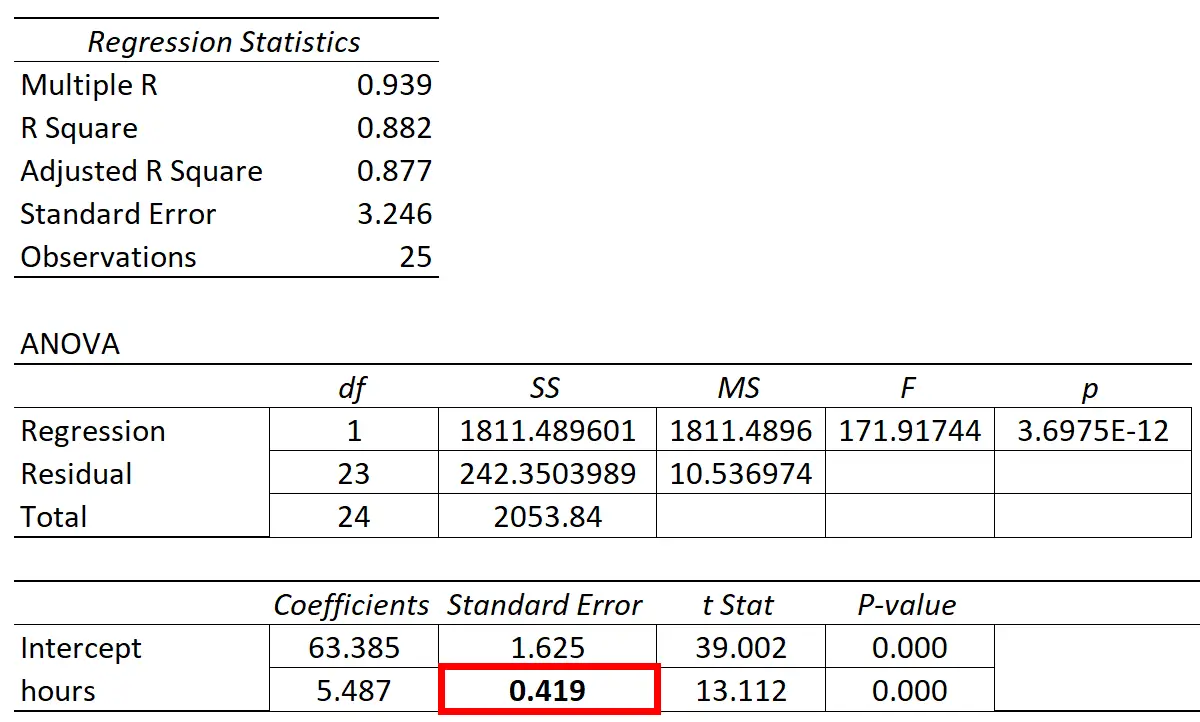
Poniższe przykłady pokazują, jak interpretować błąd standardowy nachylenia regresji w dwóch różnych scenariuszach.

Przykład 1: Interpretacja małego błędu standardowego nachylenia regresji

Załóżmy, że profesor chce zrozumieć związek między liczbą przepracowanych godzin a oceną uczniów w jego klasie z egzaminu końcowego.

Zbiera dane dla 25 uczniów i tworzy następujący wykres rozrzutu:

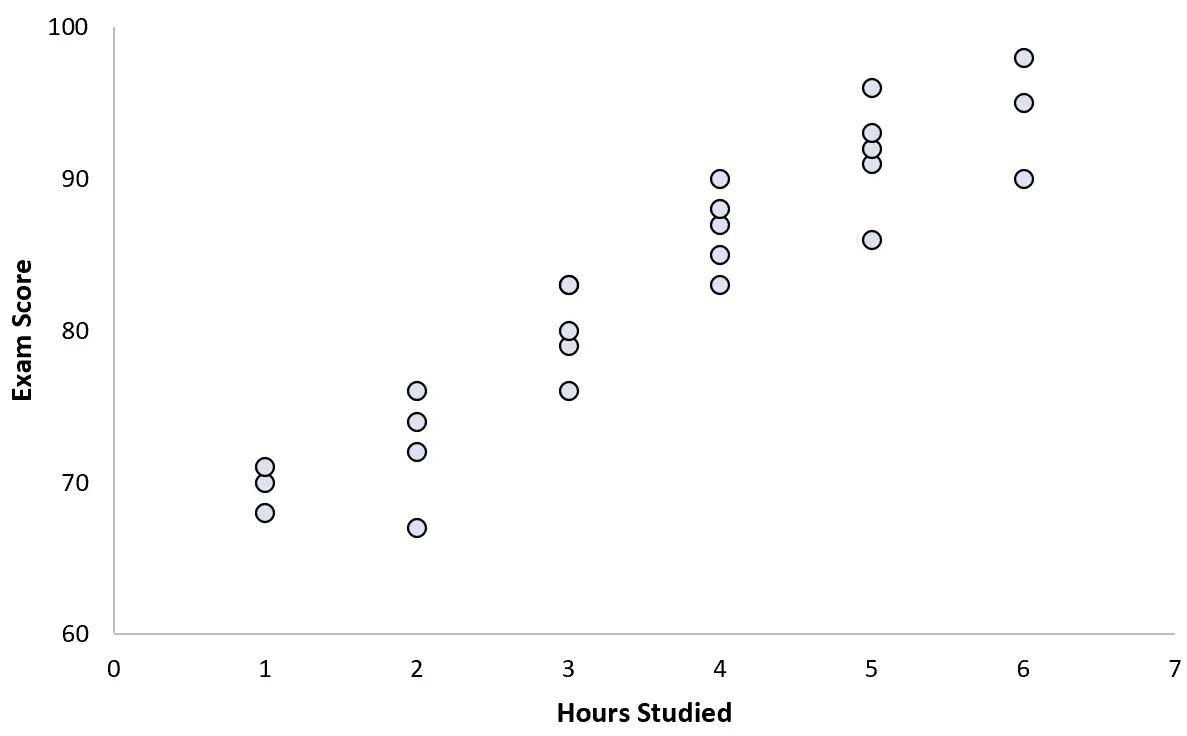
Istnieje wyraźnie pozytywny związek pomiędzy tymi dwiema zmiennymi. Wraz ze wzrostem liczby godzin nauki wynik egzaminu rośnie w dość przewidywalnym tempie.

Następnie dopasował prosty model regresji liniowej, wykorzystując przepracowane godziny jako zmienną predykcyjną i ocenę końcową z egzaminu jako zmienną odpowiedzi.

Poniższa tabela przedstawia wyniki regresji:

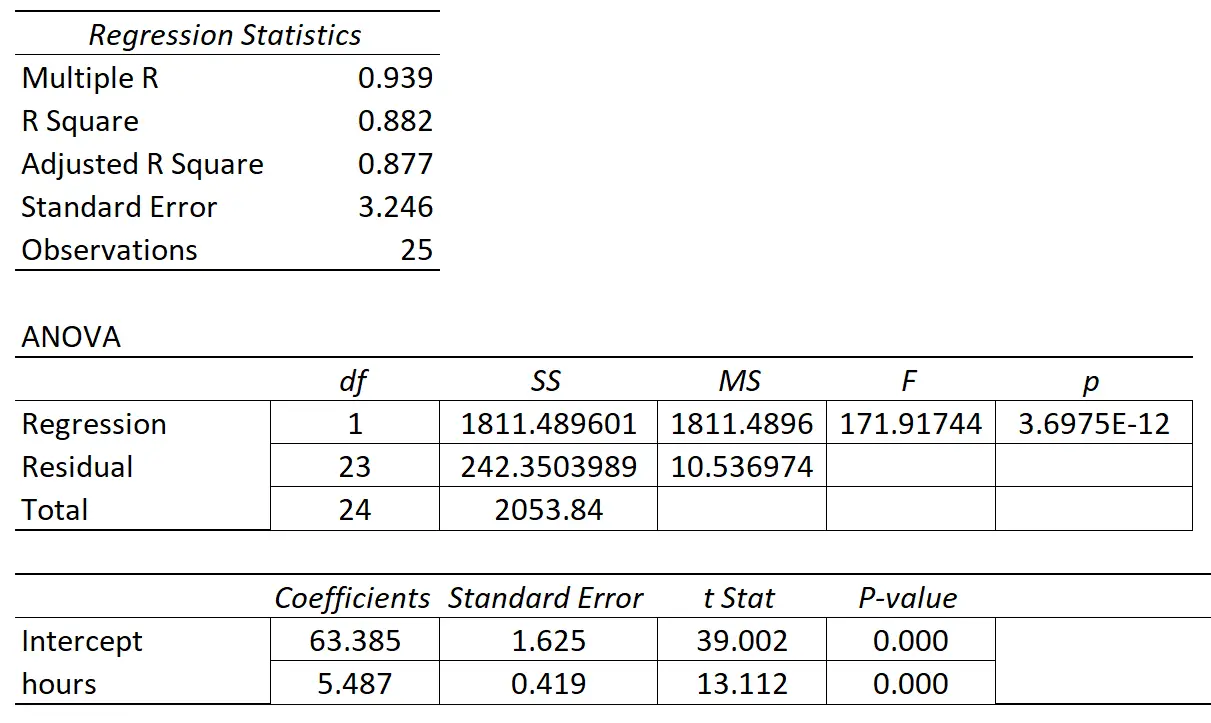
Współczynnik zmiennej predykcyjnej „godziny nauki” wynosi 5,487. To mówi nam, że każda dodatkowa godzina nauki wiąże się ze średnim wzrostem wyniku egzaminu o 5487 .

Błąd standardowy wynosi 0,419 i stanowi miarę zmienności wokół tego oszacowania nachylenia regresji.

Możemy użyć tej wartości do obliczenia statystyki t dla zmiennej predykcyjnej „przepracowane godziny”:

• t statystyka = oszacowanie współczynnika / błąd standardowy
• statystyka t = 5,487 / 0,419
• statystyka t = 13,112

Wartość p odpowiadająca tej statystyce testowej wynosi 0,000, co oznacza, że „przepracowane godziny” mają statystycznie istotny związek z oceną z egzaminu końcowego.

Ponieważ błąd standardowy nachylenia regresji był mały w porównaniu do oszacowania współczynnika nachylenia regresji, zmienna predykcyjna była istotna statystycznie.

Przykład 2: Interpretacja dużego błędu standardowego nachylenia regresji

Załóżmy, że inny profesor chce zrozumieć związek między liczbą przepracowanych godzin a oceną uczniów w jego klasie z egzaminu końcowego.

Zbiera dane dla 25 uczniów i tworzy następujący wykres rozrzutu:

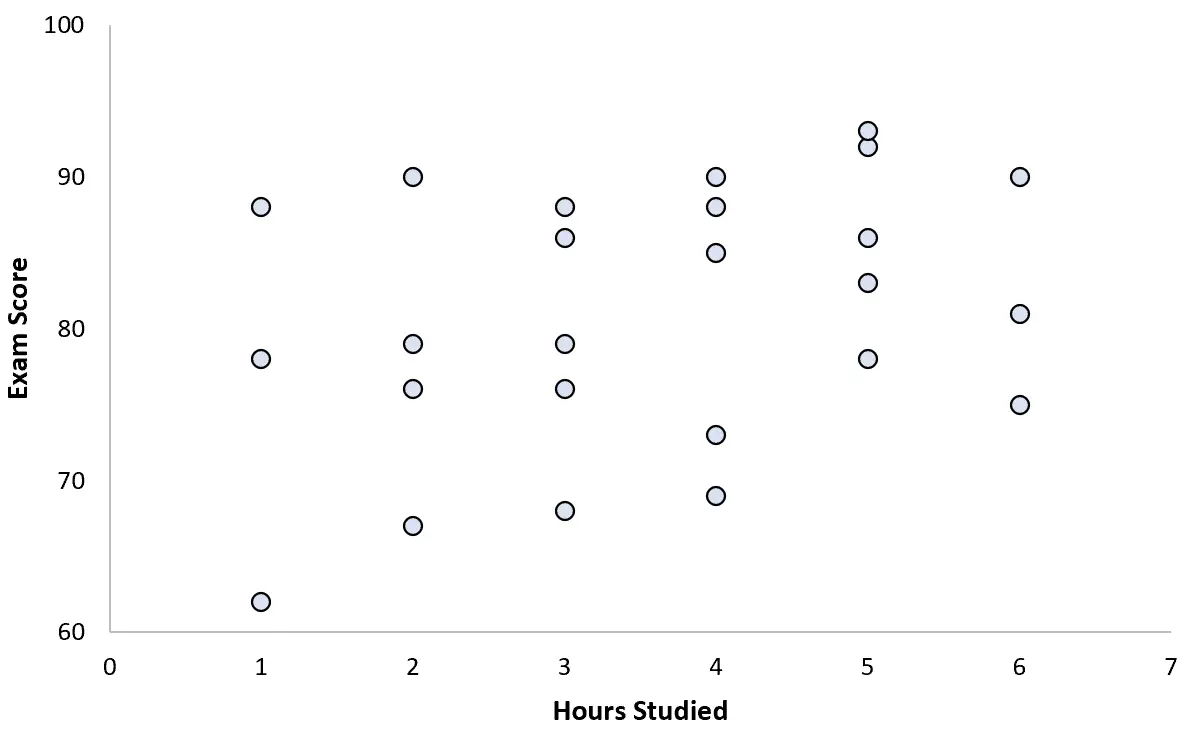
Wydaje się, że istnieje niewielka pozytywna korelacja między tymi dwiema zmiennymi. Wraz ze wzrostem liczby godzin nauki wynik egzaminu na ogół rośnie, ale nie w przewidywalnym tempie.

Załóżmy, że profesor dopasowuje następnie prosty model regresji liniowej, wykorzystując przepracowane godziny jako zmienną predykcyjną i końcową ocenę z egzaminu jako zmienną odpowiedzi.

Poniższa tabela przedstawia wyniki regresji:

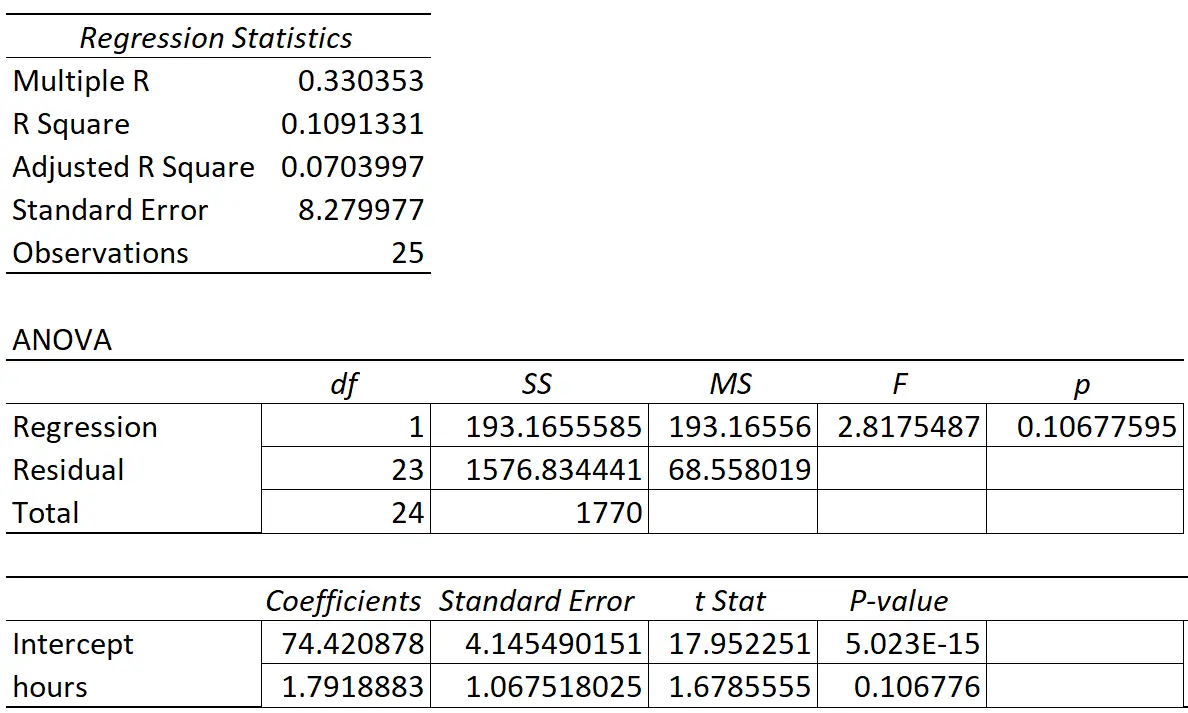
Współczynnik zmiennej predykcyjnej „godziny nauki” wynosi 1,7919. To mówi nam, że każda dodatkowa godzina nauki wiąże się ze średnim wzrostem wyniku egzaminu o 1,7919 .

Błąd standardowy wynosi 1,0675 i jest miarą zmienności wokół tego oszacowania nachylenia regresji.

Możemy użyć tej wartości do obliczenia statystyki t dla zmiennej predykcyjnej „przepracowane godziny”:

• t statystyka = oszacowanie współczynnika / błąd standardowy
• statystyka t = 1,7919 / 1,0675
• statystyka t = 1,678

Wartość p odpowiadająca tej statystyce testowej wynosi 0,107. Ponieważ ta wartość p jest nie mniejsza niż 0,05, oznacza to, że „przepracowane godziny” nie mają statystycznie istotnego związku z oceną z egzaminu końcowego.

Ponieważ błąd standardowy nachylenia regresji był duży w stosunku do oszacowania współczynnika nachylenia regresji, zmienna predykcyjna nie była istotna statystycznie.

Dodatkowe zasoby

Wprowadzenie do prostej regresji liniowej
Wprowadzenie do wielokrotnej regresji liniowej
Jak czytać i interpretować tabelę regresji