Ujemny rozkład dwumianowy

Przez Benjamin Anderson 3 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest ujemny rozkład dwumianowy i do czego się go używa. Znajdziesz tu również wzór na ujemny rozkład dwumianowy, konkretny przykład i właściwości tego typu rozkładu prawdopodobieństwa. Wreszcie, za pomocą kalkulatora internetowego będziesz mógł obliczyć dowolne prawdopodobieństwo ujemnego rozkładu dwumianowego.

Co to jest ujemny rozkład dwumianowy?

Ujemny rozkład dwumianowy to rozkład prawdopodobieństwa opisujący liczbę prób Bernoulliego wymaganych do uzyskania danej liczby pozytywnych wyników.

Dlatego ujemny rozkład dwumianowy ma dwa charakterystyczne parametry: r to liczba pożądanych pomyślnych wyników, a p to prawdopodobieństwo sukcesu dla każdego przeprowadzonego eksperymentu Bernoulliego.

$X\sim \text{BN}(r,p)$

Pamiętaj, że test Bernoulliego to eksperyment, który ma dwa możliwe wyniki: „sukces” i „porażkę”. Zatem jeśli prawdopodobieństwo „sukcesu” wynosi p , prawdopodobieństwo „porażki” wynosi q=1-p .

Zatem ujemny rozkład dwumianowy definiuje proces, w którym przeprowadza się tyle prób Bernoulliego, ile potrzeba do uzyskania pozytywnych wyników . Co więcej, wszystkie te próby Bernoulliego są niezależne i mają stałe prawdopodobieństwo powodzenia .

Na przykład zmienna losowa, która ma ujemny rozkład dwumianowy, oznacza, ile razy należy rzucić kostką, aby trzykrotnie wyrzucono liczbę 6.

Różnica między ujemnym rozkładem dwumianowym a rozkładem dwumianowym polega na tym, że ujemny rozkład dwumianowy liczy, ile razy potrzeba, aby uzyskać określoną liczbę pomyślnych wyników, podczas gdy rozkład dwumianowy liczy liczbę udanych przypadków w serii testów Bernoulliego.

➤ Zobacz: Co to jest rozkład dwumianowy?

Wzór na rozkład ujemny dwumianowy

Biorąc pod uwagę parametry r, p, x, prawdopodobieństwo ujemnego rozkładu dwumianowego oblicza się, mnożąc liczbę kombinatoryczną x-1 w xr przez (1-p) ^xr przez p ^r .

Zatem wzór na obliczenie prawdopodobieństwa ujemnego rozkładu dwumianowego jest następujący:

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć prawdopodobieństwo wystąpienia zmiennej o ujemnym rozkładzie dwumianowym.

Rozwiązane ćwiczenie ujemnego rozkładu dwumianowego

Jakie jest prawdopodobieństwo, że jeśli rzucisz monetą osiem razy, to w ósmym rzucie wypadnie reszka za czwartym razem?

Najpierw musimy obliczyć prawdopodobieństwo wyrzucenia orła podczas rzucania monetą. W tym przypadku mamy tylko jeden pozytywny wynik (reszka) z dwóch możliwych wyników (reszka i reszka), więc prawdopodobieństwo sukcesu wynosi:

$p=\cfrac{1}{2}=0,5$

Zatem zmienna losowa w tym problemie ma ujemny rozkład dwumianowy, gdzie r=4 i p=0,5. Dlatego używamy wzoru ujemnego rozkładu dwumianowego do obliczenia prawdopodobieństwa wymaganego w ćwiczeniu.

$\begin{aligned}P[X=x]&=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r\\[2ex]\displaystyle P[X=8]&=\begin{pmatrix}8-1\\ 8-4\end{pmatrix}\cdot (1-0,5)^{8-4}\cdot 0,5^4\\[2ex] P[X=8]&=0,1367\end{aligned}$

Charakterystyka ujemnego rozkładu dwumianowego

Poniżej znajdują się najważniejsze cechy ujemnego rozkładu dwumianowego.

Ujemny rozkład dwumianowy jest definiowany przez dwa charakterystyczne parametry: r jest liczbą pożądanych pomyślnych wyników, a p jest prawdopodobieństwem sukcesu dla każdego przeprowadzonego eksperymentu Bernoulliego.

 *** QuickLaTeX cannot compile formula:
\begin{array}{c}r\in \mathbb{Z}^+ \\[2ex] 0 <ul><li> The mean of the negative binomial distribution is equal to <em>r</em> multiplied by <em>(1-p)</em> and divided by <em>p</em> . Thus the formula which makes it possible to calculate the mean of a negative binomial distribution is the following: </li></ul>[latex]E[X]=\cfrac{r\cdot (1-p)}{p}

*** Error message:
Missing $ inserted.
leading text: \begin{array}{c}
Please use \mathaccent for accents in math mode.
leading text: ...The mean of the binomial distribution born
Please use \mathaccent for accents in math mode.
leading text: ... the negative binomial distribution is
Please use \mathaccent for accents in math mode.
leading text: ...negative binomial distribution is equal to
Please use \mathaccent for accents in math mode.
leading text: ...gative is equal to <em>r</em> multiplied
Please use \mathaccent for accents in math mode.
leading text: ...m> multiplied by <em>(1-p)</em> and divided
Please use \mathaccent for accents in math mode.
leading text: ...the mean of a binomial distribution born
\begin{array} on input line 8 ended by \end{document}.

Wariancja ujemnego rozkładu dwumianowego jest równa r pomnożonym przez (1-p) podzielonym przez p ² .

$Var(X)=\cfrac{r\cdot (1-p)}{p^2}$

Jeżeli parametr r jest większy od 1, postać ujemnego rozkładu dwumianowego można obliczyć ze wzoru:

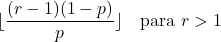
$\displaystyle \lfloor \frac{(r-1)(1-p)}{p}\rfloor\quad \text{para }r>1″ title=”Rendered by QuickLaTeX.com” height=”42″ width=”221″ style=”vertical-align: -16px;”></p> </p> <ul> <li> Funkcja masy pozwalająca określić prawdopodobieństwo wystąpienia ujemnego rozkładu dwumianowego jest następująca:</li> </ul> <p class=$ $P[X=x]=\begin{pmatrix}x-1\\ x-r\end{pmatrix}\cdot (1-p)^{x-r}\cdot p^r$

Współczynnik skośności ujemnego rozkładu dwumianowego oblicza się za pomocą następującego wyrażenia:

$\displaystyle A=\frac{2-p}{\sqrt{r\,(1-p)}}$

Kurtozę ujemnego rozkładu dwumianowego można znaleźć za pomocą następującego wzoru:

$\displaystyle C=\frac{6}{r} + \frac{p^2}{r\,(1-p)}$

Jeżeli parametr r jest równy 1, to mamy przypadek rozkładu geometrycznego .

$r=1 \quad\color{orange}\bm{\longrightarrow}\color{black}\quad X\sim \text{Geometrica}(p)$

Kalkulator ujemnego rozkładu dwumianowego

Wprowadź wartości parametrów r, p, x do poniższego kalkulatora, aby obliczyć prawdopodobieństwo. Należy wprowadzić liczby, używając kropki jako separatora dziesiętnego, na przykład 0,50.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej