Rozkład dwumianowy

Przez Benjamin Anderson 3 sierpnia, 2023 Prawdopodobieństwo 0 komentarzy

W tym artykule wyjaśniono, czym jest rozkład dwumianowy w statystyce i do czego się go używa. Znajdziesz zatem definicję rozkładu dwumianowego, przykłady rozkładów dwumianowych oraz właściwości tego typu rozkładu prawdopodobieństwa. Dodatkowo będziesz w stanie obliczyć dowolne prawdopodobieństwo rozkładu dwumianowego za pomocą kalkulatora online.

Co to jest rozkład dwumianowy?

Rozkład dwumianowy to rozkład prawdopodobieństwa, który oblicza liczbę sukcesów podczas wykonywania serii niezależnych, dychotomicznych eksperymentów ze stałym prawdopodobieństwem sukcesu.

Innymi słowy, rozkład dwumianowy to rozkład opisujący liczbę pomyślnych wyników sekwencji prób Bernoulliego.

Pamiętaj, że test Bernoulliego to eksperyment, który ma dwa możliwe wyniki: „sukces” i „porażkę”. Zatem, jeśli prawdopodobieństwo „sukcesu” wynosi p , prawdopodobieństwo „porażki” wynosi q=1-p .

Ogólnie rzecz biorąc, całkowitą liczbę przeprowadzonych eksperymentów definiuje się za pomocą parametru n , natomiast p jest prawdopodobieństwem powodzenia każdego eksperymentu. Zatem zmienną losową o rozkładzie dwumianowym zapisuje się w następujący sposób:

$X\sim\text{Bin}(n,p)$

Należy zauważyć, że w rozkładzie dwumianowym dokładnie ten sam eksperyment powtarza się n razy, a eksperymenty są od siebie niezależne, zatem prawdopodobieństwo powodzenia każdego eksperymentu jest takie samo (p) .

Rozkład dwumianowy można również nazwać rozkładem dwumianowym .

Przykłady rozkładu dwumianowego

Kiedy już zapoznamy się z definicją rozkładu dwumianowego, zobaczymy kilka przykładów zmiennych zgodnych z tym typem rozkładu, aby lepiej zrozumieć tę koncepcję.

Ile razy wypadnie reszka po rzucie monetą 25 razy.
Liczba strzałów oddanych przez koszykarza, gdy 60 razy trafia do kosza z tego samego miejsca.
Ile razy otrzymamy liczbę 6, rzucając kostką 30 razy.
Liczba zaliczeń na ogólną liczbę 50 uczniów przystępujących do egzaminu.
Liczba wadliwych jednostek w próbie 100 produktów.

Wzór na rozkład dwumianowy

Biorąc pod uwagę parametry x, n, p, funkcję prawdopodobieństwa rozkładu dwumianowego definiuje się jako liczbę kombinatoryczną n w x razy p ^x razy (1-p) ^nx .

Dlatego wzór na obliczenie prawdopodobieństwa rozkładu dwumianowego jest następujący:

👉 Możesz skorzystać z poniższego kalkulatora, aby obliczyć prawdopodobieństwo wystąpienia zmiennej zgodnej z rozkładem dwumianowym.

Z drugiej strony skumulowane prawdopodobieństwo rozkładu dwumianowego oblicza się poprzez dodanie prawdopodobieństw liczby rozpatrywanych przypadków sukcesu i wszystkich poprzednich prawdopodobieństw. Zatem wzór na obliczenie skumulowanego prawdopodobieństwa rozkładu dwumianowego jest następujący:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Rozwiązane ćwiczenie z rozkładu dwumianowego

Rzucamy monetą 10 razy. Jakie jest prawdopodobieństwo, że wypadnie 6 orłów?

Zmienna w tym problemie ma rozkład dwumianowy, ponieważ wszystkie starty są od siebie niezależne i mają takie samo prawdopodobieństwo powodzenia.

Konkretnie, prawdopodobieństwo sukcesu wynosi 50%, ponieważ tylko jeden z dwóch możliwych wyników uważa się za sukces.

$p=\cfrac{1}{2}=0,5$

Dlatego rozkład dla tego ćwiczenia jest dwumianowy z łącznie 10 eksperymentami i prawdopodobieństwem 0,5.

$X\sim\text{Bin}(10 ; 0,5)$

Aby więc określić prawdopodobieństwo wyrzucenia sześciu orłów, musimy zastosować wzór na rozkład dwumianowy.

$\begin{aligned}P[X=x]&=\begin{pmatrix}n\\x\end{pmatrix}p^x(1-p)^{n-x}\\[2ex]P[X=6]&=\begin{pmatrix}10\\6\end{pmatrix}0,5^6(1-0,5)^{10-6}\\[2ex]P[X=6]&=0,2051\end{aligned}$

Zatem prawdopodobieństwo wyrzucenia dokładnie sześciu orłów w rzucie monetą dziesięć razy wynosi 20,51%.

Charakterystyka rozkładu dwumianowego

Rozkład dwumianowy ma następujące cechy:

Rozkład dwumianowy definiowany jest za pomocą dwóch parametrów: n to całkowita liczba eksperymentów Bernoulliego, a z drugiej strony p to prawdopodobieństwo powodzenia każdego eksperymentu Bernoulliego.

$\begin{array}{c}X\sim\text{Bin}(n,p)\\[2ex]n\geq 0\\[2ex]0\leq p\leq 1\end{array}$

Średnia rozkładu dwumianowego jest równa iloczynowi całkowitej liczby eksperymentów pomnożonej przez prawdopodobieństwo powodzenia każdego eksperymentu. Dlatego, aby obliczyć średnią rozkładu dwumianowego, należy pomnożyć n przez p .

$E[X]=n\cdot p$

Wariancja rozkładu dwumianowego jest równa całkowitej liczbie prób pomnożonej przez prawdopodobieństwo sukcesu i prawdopodobieństwo niepowodzenia.

$Var(X)=n\cdot p\cdot (1-p)$

Wzór na funkcję prawdopodobieństwa rozkładu dwumianowego jest następujący:

$\displaystyle P[X=x]&=\begin{pmatrix}n\\ x\end{pmatrix}p^x(1-p)^{n-x}$

Podobnie wzór na dystrybuantę rozkładu dwumianowego wygląda następująco:

$\displaystyle P[X\leq x]=\sum_{k=0}^x\begin{pmatrix}n\\k\end{pmatrix}p^k(1-p)^{n-k}$

Suma dwóch niezależnych rozkładów dwumianowych o tym samym prawdopodobieństwie jest równoważna rozkładowi dwumianowemu o tej samej wartości prawdopodobieństwa p , a n będące sumą całkowitej liczby prób dwóch rozkładów.

$\begin{array}{c}X\sim\text{Bin}(n,p)\qquad Y\sim\text{Bin}(m,p)\\[4ex]Z=X+Y \sim\text{Bin}(n+m,p)\end{array}$

$\displaystyle P[Z=z]=\begin{pmatrix}n+m\\z\end{pmatrix}p^z(1-p)^{n+m-z}$

Rozkład Bernoulliego jest szczególnym przypadkiem rozkładu dwumianowego, w którym n=1 , czyli przeprowadza się tylko jedno doświadczenie.

$X\sim\text{Bin}(1,p) \quad \color{orange}\bm{\longrightarrow}\color{black}\quad X\sim\text{Bernoulli}(p)$

_Jeżeli _X 1 , _X ₂ ,…, X _k są niezależnymi zmiennymi losowymi takimi, że

$\displaystyle\sum_{i=1}^k X_i\sim \text{Bin}\left(\sum_{i=1}^k n_i,p\right)$

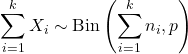
Kalkulator rozkładu dwumianowego

Wprowadź wartości parametrów p, n i x rozkładu dwumianowego do poniższego kalkulatora, aby obliczyć prawdopodobieństwo. Musisz wybrać prawdopodobieństwo, które chcesz obliczyć i wprowadzić liczby, używając kropki jako separatora dziesiętnego, na przykład 0,1667.

o autorze

Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej