5 przykładów obliczania oczekiwanej wartości w prawdziwym życiu

Wartość oczekiwana to wartość, która mówi nam o oczekiwanej średniej, którą zmienna losowa przyjmie w nieskończonej liczbie prób.

Do obliczenia oczekiwanej wartości zdarzenia używamy następującego wzoru:

Oczekiwana wartość = Σx * P(x)

Złoto:

• x : wartość danych
• P(x) : Prawdopodobieństwo wartości

Formuła ta może wydawać się nieco zagmatwana, ale nabierze większego sensu, gdy zostanie użyta w kontekście przykładów z życia codziennego.

Poniższe przykłady pokazują, jak obliczana jest wartość oczekiwana w pięciu różnych sytuacjach rzeczywistych.

Przykład 1: Inwestycje

Wartość oczekiwana jest często wykorzystywana przez firmy handlowe do określenia oczekiwanego zysku lub straty z inwestycji.

Załóżmy na przykład, że konkretna inwestycja może wygenerować roczny zwrot w wysokości 5% z prawdopodobieństwem 0,95, ale może również wygenerować roczny zwrot w wysokości -20% z prawdopodobieństwem 0,05.

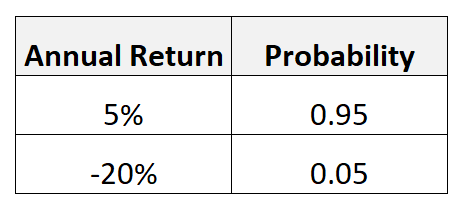
Wartość oczekiwaną tej inwestycji obliczylibyśmy w następujący sposób:

• Wartość oczekiwana = 5%*.95 + (-20%)*.05 = 3.75%

Ta konkretna inwestycja ma dodatnią wartość oczekiwaną.

Oznacza to, że gdybyśmy inwestowali w tę konkretną inwestycję nieskończoną ilość razy, oczekiwalibyśmy długoterminowej średniorocznej stopy zwrotu na poziomie 3,75%.

Przykład 2: Pogoda

Wartość oczekiwana jest często wykorzystywana przez przedsiębiorstwa rolne do określenia oczekiwanej ilości opadów, które spadną w danym sezonie.

Załóżmy na przykład, że istnieje 20% szans na 1 cal deszczu, 70% szans na 2 cale deszczu i 10% szans na 3 cale deszczu.

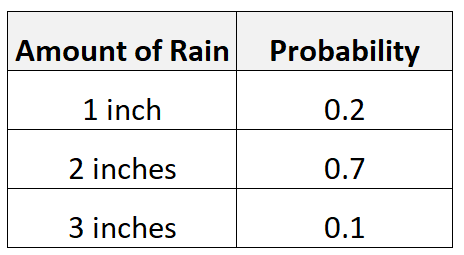
Wartość oczekiwaną ilości deszczu obliczylibyśmy w następujący sposób:

• Oczekiwana wartość = 0,2*1 + 0,7*2 + 0,1*3 = 1,9 cala

Przykład 3: Gry losowe

Wartość oczekiwana jest często wykorzystywana przez graczy do określenia, ile mogliby potencjalnie wygrać w danej grze.

Załóżmy na przykład, że w pewnej grze istnieje 5% szans na wygranie 100 dolarów, 50% szans na wygranie 0 dolarów i 45% szans na utratę 20 dolarów.

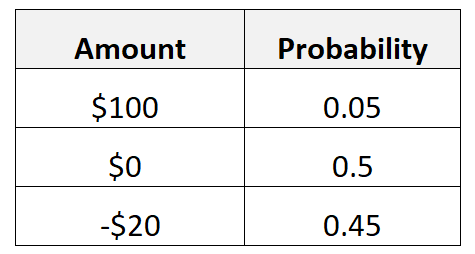
Oczekiwaną wartość zysków obliczylibyśmy w następujący sposób:

• Oczekiwana wartość = 0,05*100$ + 0,5*0$ + 0,45*(-20$) = -4$

Oznacza to, że gdybyśmy grali w tę grę nieskończoną liczbę razy, spodziewalibyśmy się średnio stracić 4 dolary za każdym razem, gdy gramy.

Przykład 4: Biznes

Wartość oczekiwana jest często wykorzystywana przez firmy do obliczania oczekiwanego zwrotu z wydatków na reklamę.

Załóżmy na przykład, że w przypadku konkretnej reklamy istnieje 10% szans na otrzymanie zwrotu w wysokości 5 USD, 30% szans na otrzymanie zwrotu w wysokości 2 USD i 60% szans na otrzymanie zwrotu w wysokości -8 USD.

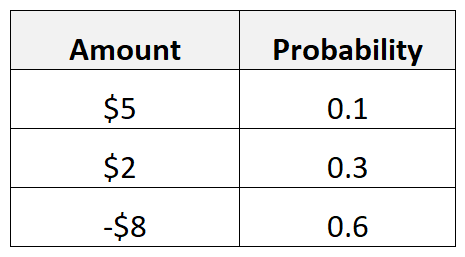
Oczekiwaną wartość reklamy obliczylibyśmy w następujący sposób:

• Oczekiwana wartość = 0,1*5$ + 0,3*2$ + 0,6*(-8$) = -3,70$

Ta konkretna reklama ma ujemną wartość oczekiwaną.

Oznacza to, że gdyby firma użyła tej konkretnej reklamy nieskończoną liczbę razy, spodziewałaby się, że za każdym razem straci średnio 3,70 dolara.

Przykład 5: Przedsiębiorczość

Wartość oczekiwana jest często wykorzystywana przez jednostki przy podejmowaniu decyzji o kontynuowaniu przedsiębiorczości.

Załóżmy na przykład, że dana osoba wierzy, że jeśli rzuci pracę i przejdzie na samozatrudnienie, ma 60% szans na zarobienie 20 000 dolarów w pierwszym roku, 30% szans na zarobienie 60 000 dolarów i 10% szans na wygranie 20 000 dolarów. 0 dolarów.

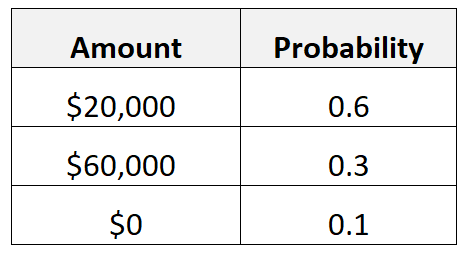
Oczekiwaną wartość ich dochodów w pierwszym roku przedsiębiorczości obliczylibyśmy w następujący sposób:

• Oczekiwana wartość = 0,6*20 000 USD + 0,3*60 000 USD + 0,1*0 USD = 30 000 USD

W zależności od tego, czy ta kwota jest wystarczająca, czy nie, osoba może następnie zdecydować się na utrzymanie obecnej pracy lub ją opuścić.

Dodatkowe zasoby

Poniższe samouczki zawierają dodatkowe informacje na temat wartości oczekiwanej:

Jak obliczyć oczekiwaną wartość w programie Excel
Jak obliczyć oczekiwaną wartość w R (z przykładami)
Wartość oczekiwana a średnia: jaka jest różnica?