Pięć założeń wielokrotnej regresji liniowej

Wielokrotna regresja liniowa to metoda statystyczna, którą możemy wykorzystać do zrozumienia związku między wieloma zmiennymi predykcyjnymi azmienną odpowiedzi .

Jednak przed wykonaniem wielokrotnej regresji liniowej musimy najpierw upewnić się, że spełnionych jest pięć założeń:

1. Zależność liniowa: Istnieje liniowa zależność pomiędzy każdą zmienną predykcyjną a zmienną odpowiedzi.

2. Brak współliniowości: żadna ze zmiennych predykcyjnych nie jest ze sobą silnie skorelowana.

3. Niezależność: Obserwacje są niezależne.

4. Homoscedastyczność: reszty mają stałą wariancję w każdym punkcie modelu liniowego.

5. Normalność wielowymiarowa: Reszty modelu mają rozkład normalny.

Jeśli jedno lub więcej z tych założeń nie zostanie spełnione, wyniki wielokrotnej regresji liniowej mogą nie być wiarygodne.

W tym artykule wyjaśniamy każde założenie, wyjaśniamy, jak ustalić, czy założenie jest spełnione i co zrobić, jeśli założenie nie jest spełnione.

Hipoteza 1: Zależność liniowa

Wielokrotna regresja liniowa zakłada, że istnieje liniowa zależność pomiędzy każdą zmienną predykcyjną a zmienną odpowiedzi.

Jak ustalić, czy to założenie jest spełnione

Najprostszym sposobem sprawdzenia, czy to założenie jest spełnione, jest utworzenie wykresu rozrzutu każdej zmiennej predykcyjnej i zmiennej odpowiedzi.

Pozwala to wizualnie sprawdzić, czy istnieje liniowa zależność między dwiema zmiennymi.

Jeśli punkty na wykresie rozrzutu leżą w przybliżeniu wzdłuż prostej linii ukośnej, prawdopodobnie istnieje liniowa zależność między zmiennymi.

Na przykład punkty na poniższym wykresie wydają się układać na linii prostej, co wskazuje, że istnieje liniowa zależność pomiędzy tą konkretną zmienną predykcyjną (x) a zmienną odpowiedzi (y):

Co zrobić, jeśli to założenie nie jest przestrzegane

Jeśli nie ma liniowej zależności między jedną lub większą liczbą zmiennych predykcyjnych a zmienną odpowiedzi, mamy kilka opcji:

1. Zastosuj transformację nieliniową do zmiennej predykcyjnej, na przykład biorąc log lub pierwiastek kwadratowy. Często może to zmienić relację na bardziej liniową.

2. Dodaj do modelu kolejną zmienną predykcyjną. Na przykład, jeśli wykres x względem y ma kształt paraboliczny, sensowne może być dodanie X ² jako dodatkowej zmiennej predykcyjnej w modelu.

3. Usuń zmienną predykcyjną z modelu. W najbardziej skrajnym przypadku, jeśli nie ma liniowej zależności pomiędzy określoną zmienną predykcyjną a zmienną odpowiedzi, wówczas uwzględnienie zmiennej predykcyjnej w modelu może nie być przydatne.

Hipoteza 2: brak współliniowości

Wielokrotna regresja liniowa zakłada, że żadna ze zmiennych predykcyjnych nie jest ze sobą silnie skorelowana.

Kiedy jedna lub więcej zmiennych predykcyjnych jest silnie skorelowanych, w modelu regresji występuje zjawisko wielowspółliniowości , co sprawia, że oszacowania współczynników modelu są niewiarygodne.

Jak ustalić, czy to założenie jest spełnione

Najprostszym sposobem sprawdzenia, czy to założenie jest spełnione, jest obliczenie wartości VIF dla każdej zmiennej predykcyjnej.

Wartości VIF zaczynają się od 1 i nie mają górnej granicy. Generalnie wartości VIF powyżej 5* wskazują na potencjalną wieloliniowość.

Poniższe samouczki pokazują, jak obliczyć VIF w różnych programach statystycznych:

• Jak obliczyć VIF w R
• Jak obliczyć VIF w Pythonie
• Jak obliczyć VIF w Excelu

*Czasami badacze używają zamiast tego wartości VIF równej 10, w zależności od kierunku studiów.

Co zrobić, jeśli to założenie nie jest przestrzegane

Jeśli jedna lub więcej zmiennych predykcyjnych ma wartość VIF większą niż 5, najłatwiejszym sposobem rozwiązania tego problemu jest po prostu usunięcie zmiennych predykcyjnych o wysokich wartościach VIF.

Alternatywnie, jeśli chcesz zachować każdą zmienną predykcyjną w modelu, możesz użyć innej metody statystycznej, takiej jak regresja grzbietowa , regresja lasso lub regresja metodą cząstkowych najmniejszych kwadratów , zaprojektowanej do obsługi wysoce skorelowanych zmiennych predykcyjnych.

Hipoteza 3: Niepodległość

Wielokrotna regresja liniowa zakłada, że każda obserwacja w zbiorze danych jest niezależna.

Jak ustalić, czy to założenie jest spełnione

Najprostszym sposobem sprawdzenia, czy to założenie jest spełnione, jest wykonanie testu Durbina-Watsona , który jest formalnym testem statystycznym, który mówi nam, czy reszty (a tym samym obserwacje) wykazują autokorelację.

Co zrobić, jeśli to założenie nie jest przestrzegane

W zależności od tego, w jaki sposób naruszone zostanie to założenie, masz kilka opcji:

• Aby uzyskać dodatnią korelację szeregową, należy rozważyć dodanie do modelu opóźnień zmiennej zależnej i/lub niezależnej.
• W przypadku ujemnej korelacji szeregowej upewnij się, że żadna ze zmiennych nie jest nadmiernie opóźniona .
• Aby uzyskać korelację sezonową, rozważ dodanie do modelu manekinów sezonowych.

Hipoteza 4: homoskedastyczność

Wielokrotna regresja liniowa zakłada, że reszty mają stałą wariancję w każdym punkcie modelu liniowego. Jeżeli tak nie jest, reszty cierpią na heteroskedastyczność .

Gdy w analizie regresji występuje heteroskedastyczność, wyniki modelu regresji stają się niewiarygodne.

W szczególności heteroskedastyczność zwiększa wariancję szacunków współczynnika regresji, ale model regresji tego nie uwzględnia. To sprawia, że znacznie bardziej prawdopodobne jest, że model regresji będzie twierdził, że składnik modelu jest istotny statystycznie, podczas gdy w rzeczywistości tak nie jest.

Jak ustalić, czy to założenie jest spełnione

Najłatwiejszym sposobem sprawdzenia, czy to założenie jest spełnione, jest utworzenie wykresu reszt standaryzowanych w funkcji przewidywanych wartości.

Po dopasowaniu modelu regresji do zbioru danych można utworzyć wykres rozrzutu, który wyświetla przewidywane wartości zmiennej odpowiedzi na osi x i reszty standaryzowane modelu na osi x. y.

Jeżeli punkty na wykresie rozrzutu wykazują tendencję, wówczas występuje heteroskedastyczność.

Poniższy wykres przedstawia przykład modelu regresji, w którym heteroskedastyczność nie stanowi problemu:

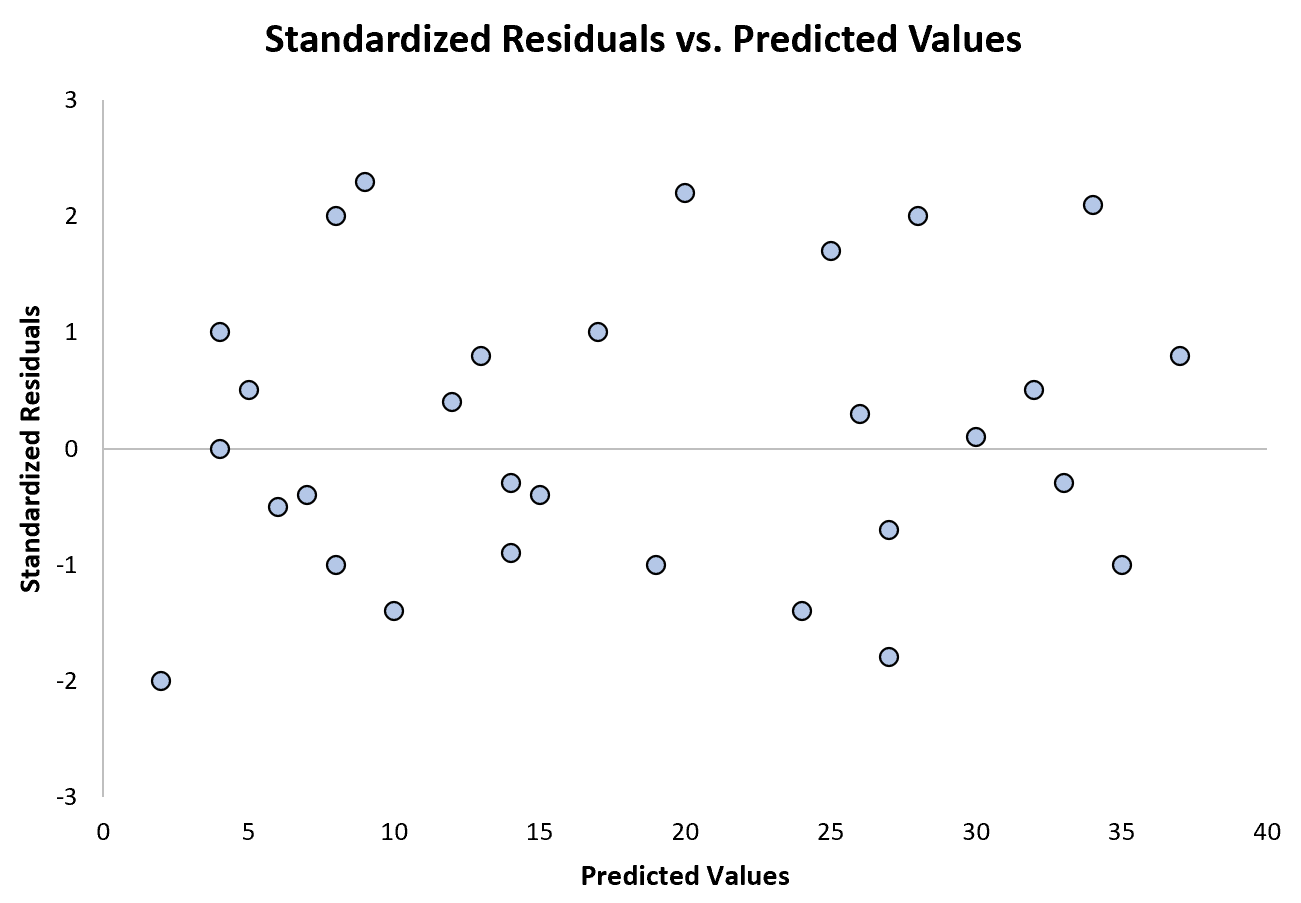
Należy zauważyć, że reszty standaryzowane są rozproszone wokół zera bez wyraźnego wzoru.

Poniższy wykres przedstawia przykład modelu regresji, w którym problemem jest heteroskedastyczność:

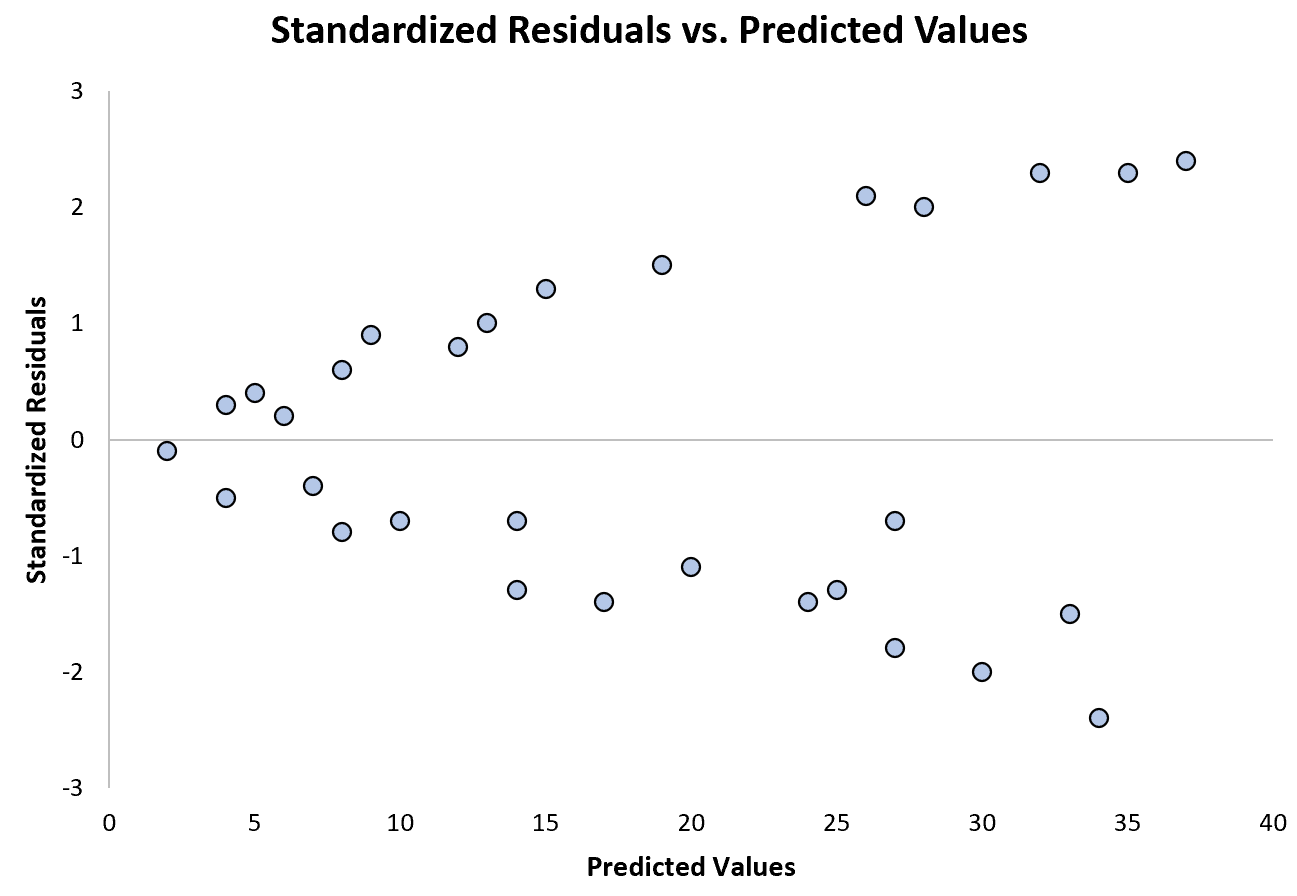
Zwróć uwagę, jak reszty standaryzowane rozprzestrzeniają się coraz bardziej wraz ze wzrostem przewidywanych wartości. Ten kształt „stożka” jest klasycznym znakiem heteroskedastyczności:

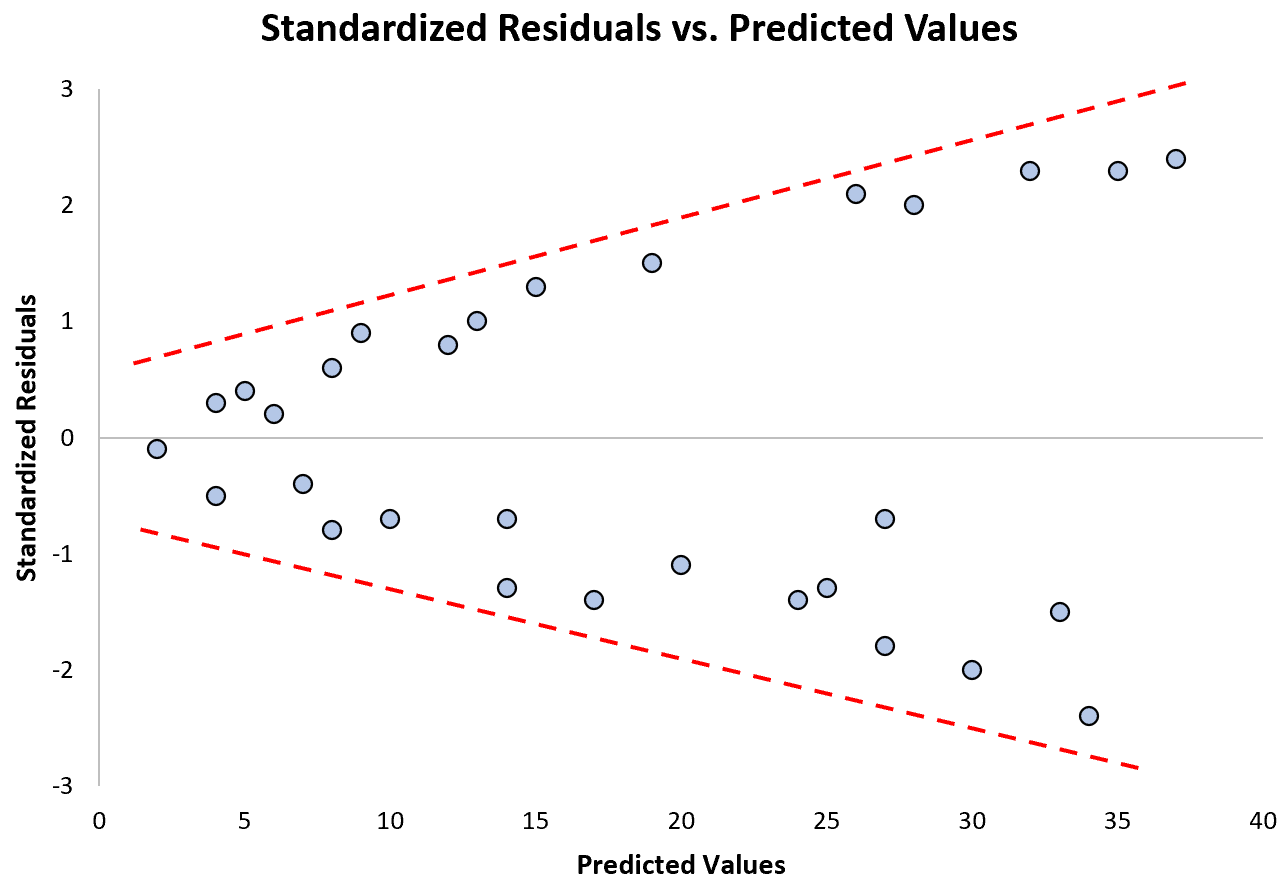
Co zrobić, jeśli to założenie nie jest przestrzegane

Istnieją trzy typowe sposoby korygowania heteroskedastyczności:

1. Przekształć zmienną odpowiedzi. Najczęstszym sposobem radzenia sobie z heteroskedastycznością jest przekształcenie zmiennej odpowiedzi poprzez pobranie logarytmu, pierwiastka kwadratowego lub pierwiastka sześciennego ze wszystkich wartości zmiennej odpowiedzi. Prowadzi to często do zaniku heteroskedastyczności.

2. Zdefiniuj na nowo zmienną odpowiedzi. Jednym ze sposobów ponownego zdefiniowania zmiennej odpowiedzi jest użycie współczynnika , a nie wartości surowej. Na przykład zamiast używać wielkości populacji do przewidywania liczby kwiaciarni w mieście, możemy użyć wielkości populacji do przewidywania liczby kwiaciarni na mieszkańca.

W większości przypadków zmniejsza to zmienność, która naturalnie występuje w większych populacjach, ponieważ mierzymy liczbę kwiaciarni na osobę, a nie samą liczbę kwiaciarni.

3. Zastosuj regresję ważoną. Innym sposobem skorygowania heteroskedastyczności jest użycie regresji ważonej, która przypisuje wagę każdemu punktowi danych na podstawie wariancji jego dopasowanej wartości.

Zasadniczo nadaje to niskie wagi punktom danych o większych wariancjach, zmniejszając ich kwadraty resztowe. Zastosowanie odpowiednich wag może wyeliminować problem heteroskedastyczności.

Powiązane : Jak przeprowadzić regresję ważoną w R

Założenie 4: Wielowymiarowa normalność

Wielokrotna regresja liniowa zakłada, że reszty modelu mają rozkład normalny.

Jak ustalić, czy to założenie jest spełnione

Istnieją dwa popularne sposoby sprawdzenia, czy to założenie jest spełnione:

1. Wizualnie zweryfikuj hipotezę za pomocą wykresów QQ .

Wykres QQ, skrót od wykresu kwantylowo-kwantylowego, to rodzaj wykresu, którego możemy użyć do określenia, czy reszty modelu mają rozkład normalny. Jeżeli punkty na wykresie tworzą w przybliżeniu prostą ukośną, wówczas spełnione jest założenie normalności.

Poniższy wykres QQ przedstawia przykład reszt, które w przybliżeniu odpowiadają rozkładowi normalnemu:

Jednakże poniższy wykres QQ przedstawia przykład przypadku, w którym reszty wyraźnie odbiegają od prostej linii ukośnej, co wskazuje, że nie są zgodne z rozkładem normalnym:

2. Zweryfikuj hipotezę za pomocą formalnego testu statystycznego, takiego jak Shapiro-Wilk, Kołmogorow-Smironow, Jarque-Barre lub D’Agostino-Pearson.

Należy pamiętać, że testy te są wrażliwe na próbki o dużej wielkości – to znaczy często stwierdzają, że reszty nie są normalne, gdy wielkość próbki jest wyjątkowo duża. Dlatego często łatwiej jest zastosować metody graficzne, takie jak wykres QQ, aby zweryfikować tę hipotezę.

Co zrobić, jeśli to założenie nie jest przestrzegane

Jeżeli założenie o normalności nie jest spełnione, masz kilka możliwości:

1. Najpierw sprawdź, czy w danych nie występują skrajne wartości odstające, które powodują naruszenie założenia normalności.

2. Następnie możesz zastosować nieliniową transformację zmiennej odpowiedzi, na przykład pobierając pierwiastek kwadratowy, log lub pierwiastek sześcienny ze wszystkich wartości zmiennej odpowiedzi. Często skutkuje to bardziej normalnym rozkładem reszt modelu.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji na temat wielokrotnej regresji liniowej i jej założeń:

Wprowadzenie do wielokrotnej regresji liniowej
Przewodnik po heteroskedastyczności w analizie regresji
Przewodnik po wielowspółliniowości i VIF w regresji

Poniższe samouczki zawierają przykłady krok po kroku wykonywania wielokrotnej regresji liniowej przy użyciu różnych programów statystycznych:

Jak wykonać wielokrotną regresję liniową w programie Excel
Jak wykonać wielokrotną regresję liniową w R
Jak wykonać wielokrotną regresję liniową w SPSS
Jak wykonać wielokrotną regresję liniową w Stata