Pięć hipotez korelacji pearsona
Współczynnik korelacji Pearsona (znany również jako „współczynnik korelacji iloczynu momentu”) mierzy liniową zależność między dwiema zmiennymi.
Zawsze przyjmuje wartość z zakresu od -1 do 1, gdzie:
- -1 oznacza całkowicie ujemną korelację liniową pomiędzy dwiema zmiennymi
- Wartość 0 oznacza brak liniowej korelacji pomiędzy dwiema zmiennymi
- 1 wskazuje doskonale dodatnią korelację liniową pomiędzy dwiema zmiennymi
Jednak przed obliczeniem współczynnika korelacji Pearsona między dwiema zmiennymi musimy upewnić się, że spełnionych jest pięć założeń:
1. Poziom pomiaru: Obie zmienne należy mierzyć na poziomie przedziału lub współczynnika .
2. Zależność liniowa: Musi istnieć liniowa zależność pomiędzy dwiema zmiennymi.
3. Normalność: obie zmienne powinny mieć rozkład w przybliżeniu normalny.
4. Powiązane pary: Każda obserwacja w zbiorze danych musi mieć parę wartości.
5. Brak wartości odstających: w zbiorze danych nie powinny znajdować się skrajne wartości odstające.
W tym artykule przedstawiamy wyjaśnienie każdego założenia, a także sposób ustalenia, czy założenie jest spełnione.
Hipoteza 1: Poziom pomiaru
Aby obliczyć współczynnik korelacji Pearsona między dwiema zmiennymi, obie zmienne należy zmierzyć na poziomie przedziału lub stosunku .
Poniższa grafika zawiera szybkie wyjaśnienie czterech poziomów, na których można mierzyć zmienne:
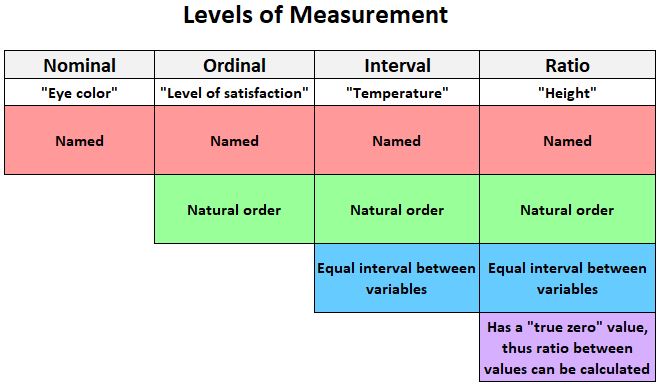
Oto kilka przykładów zmiennych, które można zmierzyć na skali interwałowej :
- Temperatura: mierzona w stopniach Fahrenheita lub Celsjusza
- Ocena kredytowa: mierzona od 300 do 850
- Wyniki SAT: mierzone od 400 do 1600
Oto kilka przykładów zmiennych, które można zmierzyć na skali ilorazowej :
- Wzrost: mierzony w centymetrach, calach, stopach itp.
- Waga: mierzona w kilogramach, funtach itp.
- Długość: mierzona w centymetrach, calach, stopach itp.
Jeśli zmienne mierzone są na poziomie porządkowym , należy obliczyć współczynnik korelacji Spearmana między nimi.
Powiązane: Poziomy pomiaru: nominalny, porządkowy, interwałowy i współczynnik
Hipoteza 2: Zależność liniowa
Aby obliczyć współczynnik korelacji Pearsona między dwiema zmiennymi, musi istnieć liniowa zależność między tymi dwiema zmiennymi.
Najprostszym sposobem sprawdzenia tej hipotezy jest po prostu utworzenie wykresu rozrzutu dwóch zmiennych. Jeżeli punkty na wykresie układają się w przybliżeniu w linii prostej, to istnieje zależność liniowa:
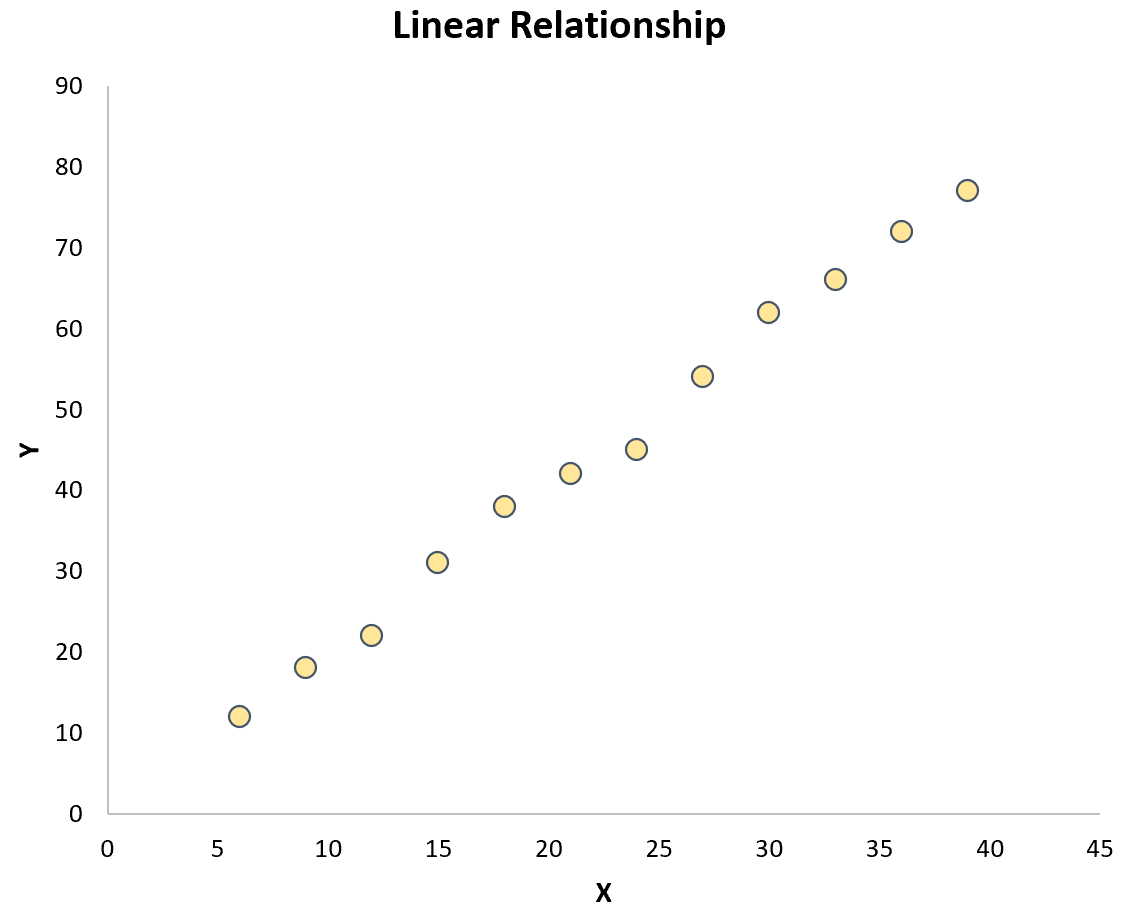
Jeśli jednak punkty są losowo rozproszone na wykresie lub mają inny rodzaj zależności (np. kwadratową), wówczas między zmiennymi nie istnieje zależność liniowa:
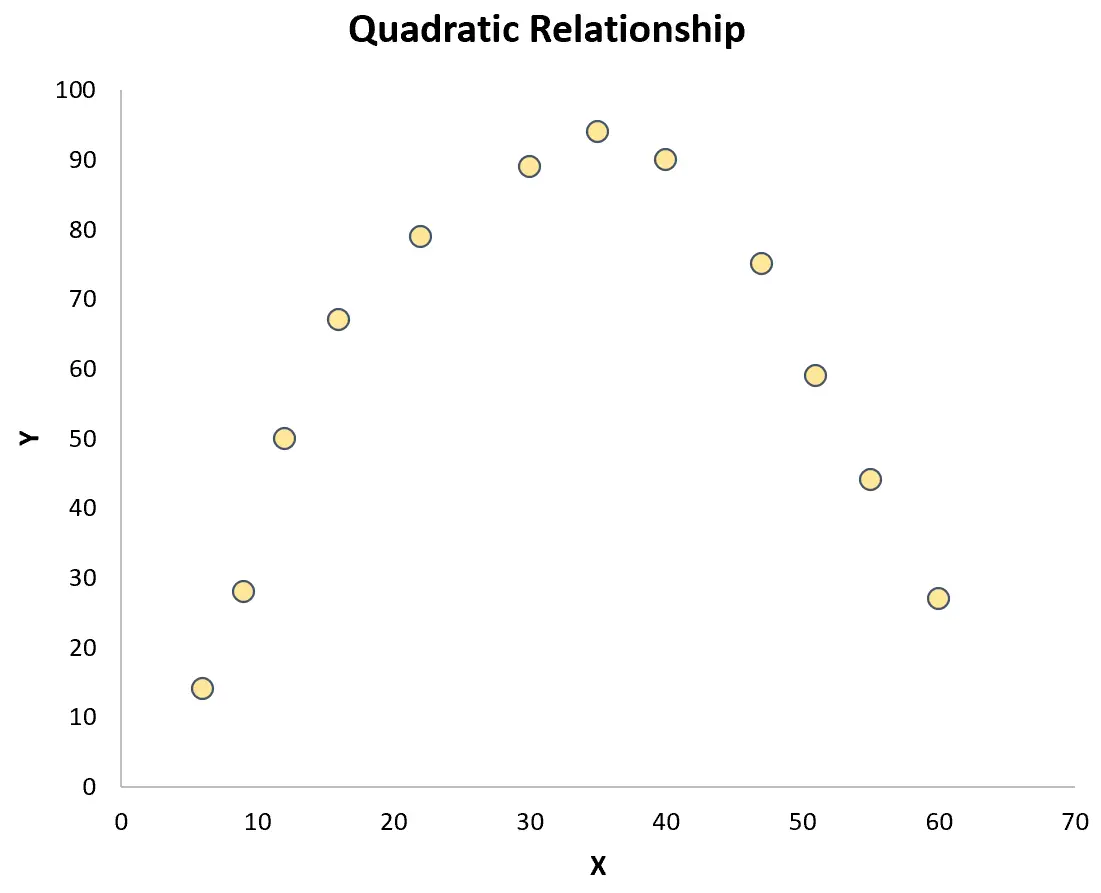
W tym przypadku współczynnik korelacji Pearsona nie będzie odpowiednio uchwycił związku między zmiennymi.
Hipoteza 3: normalność
Współczynnik korelacji Pearsona zakłada również, że te dwie zmienne mają w przybliżeniu rozkład normalny .
Możesz zweryfikować to założenie wizualnie, tworząc histogram lub wykres QQ dla każdej zmiennej.
1. Histogram
Jeśli histogram zbioru danych ma z grubsza kształt dzwonu, prawdopodobne jest, że dane mają rozkład normalny.

2. QQLand
Wykres QQ, skrót od „kwantyl-kwantyl”, to rodzaj wykresu przedstawiający teoretyczne kwantyle wzdłuż osi x (tzn. miejsce, w którym znajdowałyby się dane, gdyby miały rozkład normalny) oraz kwantyle próbek wzdłuż osi y. (tj. gdzie faktycznie znajdują się Twoje dane).
Jeżeli wartości danych przebiegają mniej więcej po linii prostej tworzącej kąt 45 stopni, wówczas zakłada się, że dane mają rozkład normalny.

Można także przeprowadzić formalny test statystyczny, aby określić, czy zmienna ma rozkład normalny.
Jeśli wartość p testu jest poniżej pewnego poziomu istotności (takiego jak α = 0,05), wówczas masz wystarczające dowody, aby stwierdzić, że dane nie mają rozkładu normalnego.
Istnieją trzy testy statystyczne powszechnie stosowane do testowania normalności:
1. Test Jarque’a-Bery
- Jak wykonać test Jarque-Bera w programie Excel
- Jak wykonać test Jarque-Bera w R
- Jak wykonać test Jarque-Bera w Pythonie
2. Test Shapiro-Wilka
3. Test Kołmogorowa-Smirnowa
Hipoteza 4: Powiązane pary
Współczynnik korelacji Pearsona zakłada również, że każda obserwacja w zbiorze danych musi mieć parę wartości.
Hipotezę tę można łatwo zweryfikować. Na przykład, jeśli obliczasz korelację między wagą a wzrostem, po prostu sprawdź, czy każda obserwacja w zbiorze danych ma miarę wagi i miarę wzrostu.
Hipoteza 5: Brak wartości odstających
Współczynnik korelacji Pearsona zakłada również, że w zbiorze danych nie ma skrajnych wartości odstających, ponieważ wartości odstające silnie wpływają na obliczenie współczynnika korelacji.
Aby to zilustrować, rozważ następujący zbiór danych:
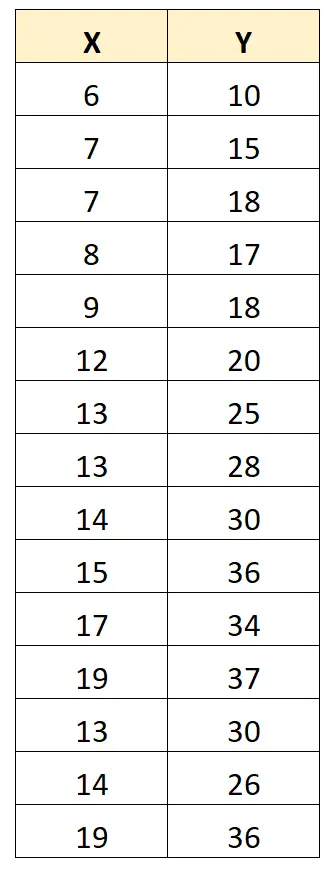
Współczynnik korelacji Pearsona pomiędzy X i Y wynosi 0,949 .
Załóżmy jednak, że w zbiorze danych mamy wartość odstającą:
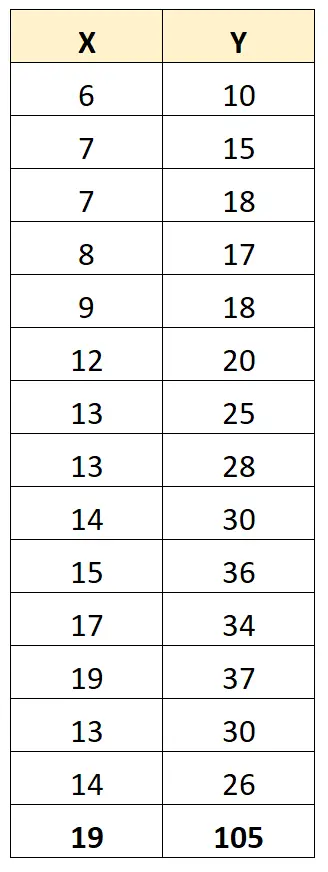
Współczynnik korelacji Pearsona pomiędzy X i Y wynosi obecnie 0,711 .
Wartość odstająca znacząco zmienia współczynnik korelacji Pearsona między dwiema zmiennymi. W takim przypadku rozsądne może być usunięcie wartości odstającej ze zbioru danych.
Powiązane: Kompletny przewodnik: Kiedy usunąć wartości odstające z danych
Dodatkowe zasoby
Poniższe samouczki zawierają dodatkowe informacje na temat korelacji Pearsona:
Wprowadzenie do współczynnika korelacji Pearsona
Jak zgłosić korelację Pearsona w formacie APA
Jak ręcznie obliczyć współczynnik korelacji Pearsona