Przedział ufności dla proporcji

Przez 3 sierpnia, 2023 Statystyka 0 komentarzy

W tym artykule wyjaśniono, czym jest przedział ufności dla proporcji i do czego służy w statystyce. Podobnie dowiesz się, jak obliczyć przedział ufności proporcji, a także rozwiązane ćwiczenie, aby lepiej zrozumieć tę koncepcję.

Jaki jest przedział ufności proporcji?

Przedział ufności dla proporcji to przedział, który zapewnia zakres dopuszczalnych wartości dla proporcji populacji. Oznacza to, że przedział ufności dla proporcji wskazuje wartość maksymalną i minimalną, pomiędzy którymi proporcja populacji mieści się z marginesem błędu.

Na przykład, jeśli przedział ufności dla odsetka populacji o poziomie ufności 95% wynosi (0,73; 0,81), oznacza to, że odsetek populacji mieści się w przedziale od 73% do 81% z prawdopodobieństwem 95%.

Dlatego też do oszacowania wartości odsetka populacji spełniającej określone cechy wykorzystuje się przedział ufności proporcji.

Jak zobaczymy w następnej sekcji, przedział ufności dla proporcji zależy od proporcji próby i liczby obserwacji w próbie.

Wzór na przedział ufności dla proporcji

Przedział ufności dla proporcji oblicza się, dodając i odejmując od proporcji próbki wartość Z α/2 pomnożoną przez pierwiastek kwadratowy proporcji próbki (p) pomnożony przez 1-p i podzielony przez liczebność próby (n). Zatem wzór na obliczenie przedziału ufności dla proporcji jest następujący:

\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)

Złoto:

  • p

    jest proporcją próbki.

  • n

    to wielkość próbki.

  • Z_{\alpha/2}

    jest kwantylem standardowego rozkładu normalnego odpowiadającym prawdopodobieństwu α/2. Dla dużych próbek i poziomu ufności 95% jest to zwykle bliskie 1,96, a dla poziomu ufności 99% jest zwykle bliskie 2,576.

Przykład obliczenia przedziału ufności dla proporcji

Abyś mógł zobaczyć, jak obliczany jest przedział ufności dla proporcji, poniżej przedstawiamy konkretny przykład krok po kroku.

  • Firma ubezpieczeniowa chce przeprowadzić badanie rynku i ustalić, ile osób w danym kraju posiada ubezpieczenie na życie. W tym celu poddaje się analizie losową próbę 700 osób i dochodzimy do wniosku, że 40% tej próby posiada ubezpieczenie na życie. Jaki jest przedział ufności przy poziomie ufności 95% dla odsetka ludności kraju?

Aby określić przedział ufności proporcji populacji, musimy skorzystać ze wzoru, który widzieliśmy powyżej:

\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)

W tym przypadku chcemy, aby poziom ufności przedziału ufności wynosił 95%, więc wartość Z α/2 , którą musimy przyjąć, wynosi 1,96.

1-\alpha=0,95 \ \color{orange}\bm{\longrightarrow}\color{black} \ \alpha=0,05 \ \color{orange}\bm{\longrightarrow}\color{black}\ \alpha/2=0,025

\begin{array}{c}Z_{\alpha/2}= \ \color{orange}\bm{?}\\[4ex]Z_{0,025}=1,96\end{array}

Stwierdzenie problemu mówi nam już, że wielkość próby wynosi n=700, a obserwowana proporcja w próbie wynosi p=0,40, więc podstawiamy dane do wzoru na przedział ufności dla proporcji i obliczamy granice przedziału:

\displaystyle \left(p-Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\ , \ p+Z_{\alpha/2}\sqrt{\frac{p(1-p)}{n}}\right)

\displaystyle \left(0,40-1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}}\ , \ 0,40+1,96\cdot \sqrt{\frac{0,40\cdot (1-0,40)}{700}\right)

\displaystyle \left(0,36 \ , \ 0,44\right)

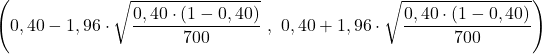
Podsumowując, odsetek badanej populacji waha się od 36% do 44% przy poziomie ufności 95%.

o autorze

Benjamin Anderson
Dr Benjamin Anderson

Cześć, jestem Benjamin i jestem emerytowanym profesorem statystyki, który został oddanym nauczycielem Statorials. Dzięki bogatemu doświadczeniu i wiedzy specjalistycznej w dziedzinie statystyki chętnie dzielę się swoją wiedzą, aby wzmocnić pozycję uczniów za pośrednictwem Statorials. Wiedzieć więcej

Dodaj komentarz

Twój adres e-mail nie zostanie opublikowany. Wymagane pola są oznaczone *