Jak ręcznie wykonać dwukierunkową anova

Dwuczynnikową analizę ANOVA stosuje się w celu określenia, czy istnieje statystycznie istotna różnica pomiędzy średnimi z trzech lub większej liczby niezależnych grup, które zostały podzielone na dwa czynniki.

W tym samouczku wyjaśniono, jak ręcznie wykonać dwukierunkową analizę ANOVA.

Przykład: ręczna dwukierunkowa ANOVA

Załóżmy, że botanik chce wiedzieć, czy na wzrost roślin wpływa ekspozycja na światło słoneczne i częstotliwość podlewania. Sadzi 40 nasion i pozwala im rosnąć przez miesiąc w różnych warunkach nasłonecznienia i częstotliwości podlewania.

Po miesiącu rejestruje wysokość każdej rośliny. Wyniki przedstawiono poniżej:

W powyższej tabeli widzimy, że w każdej kombinacji warunków hodowano pięć roślin.

Na przykład pięć roślin uprawiano przy codziennym podlewaniu i bez światła słonecznego, a ich wysokość po dwóch miesiącach wynosiła 4,8 cala, 4,4 cala, 3,2 cala, 3,9 cala i 4,4 cala:

Aby przeprowadzić dwuczynnikową analizę ANOVA, możemy wykonać następujące kroki:

Krok 1: Oblicz sumę kwadratów pierwszego współczynnika (częstotliwość podlewania)

Najpierw obliczymy ogólną średnią wysokość 40 roślin:

Ogólna średnia = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Następnie obliczymy średnią wysokość wszystkich roślin podlewanych codziennie:

Średnia dzienna = (4,8 + 5 + 6,4 + 6,3 + … + 4,4 + 4,8 + 5,8 + 5,8) /20 = 5,155

Następnie obliczymy średnią wysokość wszystkich roślin podlewanych w każdym tygodniu:

Średnia tygodniowa = (4,4 + 4,9 + 5,8 + 6 + … + 3,9 + 4,8 + 5,5 + 5,5) /20 = 5,15

Następnie obliczymy sumę kwadratów współczynnika „częstotliwości podlewania” za pomocą następującego wzoru:

Σn(X _j – X ..) ²

Złoto:

• n : liczebność próby grupy j
• Σ : grecki symbol oznaczający „sumę”
• X _j : średnia grupy j
• X .. : świetna średnia

W naszym przykładzie sumę kwadratów współczynnika „częstotliwości nawadniania” obliczamy w następujący sposób: 20(5,155-5,1525) ² + 20(5,15-5,1525) ² = 0,00025

Krok 2: Oblicz sumę kwadratów drugiego współczynnika (ekspozycja na słońce)

Najpierw obliczymy ogólną średnią wysokość 40 roślin:

Ogólna średnia = (4,8 + 5 + 6,4 + 6,3 + … + 3,9 + 4,8 + 5,5 + 5,5) / 40 = 5,1525

Następnie obliczymy średnią wysokość wszystkich roślin nie wystawionych na działanie słońca:

Średnia bez słońca = (4,8 + 4,4 + 3,2 + 3,9 + 4,4 + 4,4 + 4,2 + 3,8 + 3,7 + 3,9) / 10 = 4,07

Powtórzymy to obliczenie, aby znaleźć średnią wysokość roślin poddanych różnym ekspozycjom słonecznym:

• Niskie średnie nasłonecznienie = 5,1
• Średnie średnie nasłonecznienie = 5,89
• Średnie wysokie nasłonecznienie = 5,55

Następnie obliczymy sumę kwadratów współczynnika „nasłonecznienia” korzystając z następującego wzoru:

Σn(X _j – X ..) ²

Złoto:

• n : liczebność próby grupy j
• Σ : grecki symbol oznaczający „sumę”
• X _j : średnia grupy j
• X .. : świetna średnia

W naszym przykładzie sumę kwadratów współczynnika „nasłonecznienia” obliczamy w następujący sposób: 10(4,07-5,1525) ² + 10(5,1-5,1525) ² + 10(5,89 -5,1525) ² + 10(5,55-5,1525) ² = 18,76475

Krok 3: Oblicz sumę kwadratów wewnątrz (błąd)

Następnie obliczymy sumę kwadratów, biorąc sumę kwadratów różnic pomiędzy każdą kombinacją czynników i wysokościami poszczególnych roślin.

Przykładowo średnia wysokość wszystkich roślin podlewanych codziennie bez ekspozycji na światło słoneczne wynosi 4,14. Możemy następnie obliczyć sumę kwadratów różnic dla każdej z tych poszczególnych roślin w następujący sposób:

• SS do codziennego podlewania i bez słońca: (4,8-4,14) ² + (4,4-4,14) ² + (3,2-4,14) ² + (3,9-4,14) ² + (4,4-4,14) ² = 1,512

Możemy powtórzyć ten proces dla każdej kombinacji czynników:

• SS do codziennego podlewania i przy słabym nasłonecznieniu: 0,928
• SS dla codziennego podlewania i średniego nasłonecznienia: 1788
• SS do codziennego podlewania i silnego nasłonecznienia: 1.648
• SS dla cotygodniowego podlewania bez słońca: 0,34
• SS dla cotygodniowego podlewania i niskiego nasłonecznienia: 0,548
• SS dla cotygodniowego podlewania i średniego nasłonecznienia: 0,652
• SS dla cotygodniowego podlewania i silnego nasłonecznienia: 1268

Możemy wtedy zsumować wszystkie te wartości, aby znaleźć sumę kwadratów w środku (błąd):

Sumy kwadratów w obrębie = 1,512 + 0,928 + 1,788 + 1,648 + 0,34 + 0,548 + 0,652 + 1,268 = 8,684

Krok 4: Oblicz całkowitą sumę kwadratów

Następnie możemy obliczyć całkowitą sumę kwadratów, biorąc sumę różnic między wysokością każdej rośliny a średnią ogólną:

Całkowita suma kwadratów = (4,8 – 5,1525) ² + (5 – 5,1525) ² + … + (5,5 – 5,1525) ² = 28,45975

Krok 5: Oblicz sumę kwadratów interakcji

Następnie obliczymy sumę kwadratów interakcji, korzystając z następującego wzoru:

• Interakcja SS = SS ogółem – współczynnik SS 1 – współczynnik SS 2 – wnętrze SS
• Interakcja SS = 28,45975 – 0,00025 – 18,76475 – 8,684
• Interakcja SS = 1,01075

Krok 6: Wypełnij tabelę ANOVA

Na koniec uzupełnimy wartości z dwukierunkowej tabeli ANOVA:

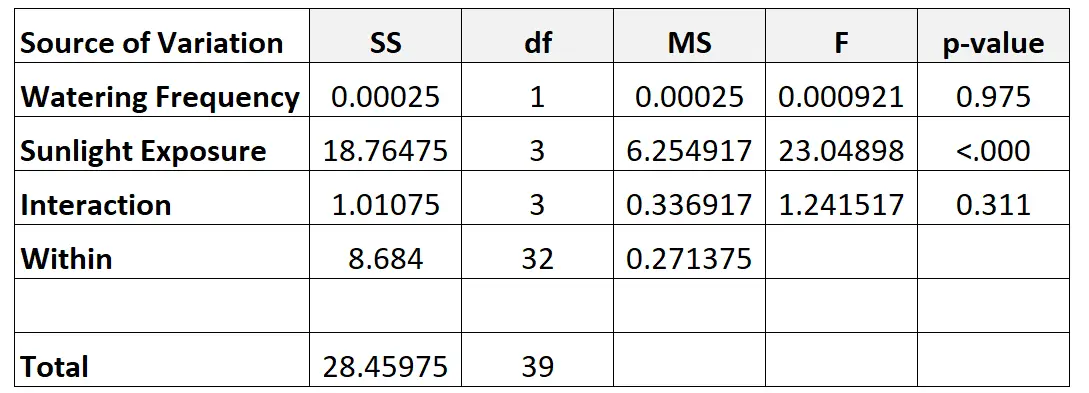
Oto jak obliczyliśmy różne liczby w tabeli:

• df Częstotliwość nawadniania: d-1 = 2-1 = 1
• df Ekspozycja na słońce: k-1 = 4-1 = 3
• dfInterakcja : (j-1)*(k-1) = 1*3 = 3
• df In : n – (j*k) = 40 – (2*4) = 32
• całkowity df: n-1 = 40-1 = 39
• MS: SS/DF
• Częstotliwość nawadniania F : częstotliwość nawadniania MS/MS w pomieszczeniu
• F Ekspozycja na światło słoneczne : MS / MS ekspozycja na światło słoneczne w pomieszczeniu
• Interakcja F : Interakcja MS / MS Wewnątrz
• wartość p częstotliwość nawadniania : wartość p odpowiadająca wartości F wynoszącej 0,000921 z licznikiem df = 1 i mianownikiem df = 32
• Wartość p ekspozycji na słońce : wartość p odpowiadająca wartości F wynoszącej 23,04898 z licznikiem df = 3 i mianownikiem df = 32
• Interakcja wartości p : Wartość p odpowiadająca wartości F wynoszącej 1,241517 z licznikiem df = 3 i mianownikiem df = 32

Uwaga nr 1: n = całkowita liczba obserwacji, j = liczba poziomów częstotliwości podlewania, k = liczba poziomów ekspozycji na słońce.

Uwaga nr 2 : Wartości p odpowiadające wartości F zostały obliczone przy użyciu kalkulatora rozkładu F.

Krok 7: Interpretacja wyników

Z tabeli ANOVA możemy zaobserwować, co następuje:

• Wartość p dla interakcji pomiędzy częstotliwością podlewania a ekspozycją na słońce wyniosła 0,311 . Nie jest to istotne statystycznie przy α = 0,05.
• Wartość p dla częstotliwości podlewania wyniosła 0,975 . Nie jest to istotne statystycznie przy α = 0,05.
• Wartość p dla ekspozycji na słońce wynosiła <0,000 . Jest to statystycznie istotne przy α = 0,05.

Wyniki te wskazują, że ekspozycja na słońce jest jedynym czynnikiem mającym statystycznie istotny wpływ na wysokość roślin.

A ponieważ nie ma efektu interakcji, wpływ ekspozycji na słońce jest stały na każdym poziomie częstotliwości podlewania.

Mówiąc najprościej, to, czy roślina jest podlewana codziennie, czy co tydzień, nie ma wpływu na wpływ ekspozycji na słońce na roślinę.

Dodatkowe zasoby

Poniższe tutoriale dostarczają dodatkowych informacji na temat ANOVA:

Jak ręcznie wykonać jednokierunkową ANOVA
Jak ręcznie wykonać ANOVA z powtarzanymi pomiarami
Kompletny przewodnik: Jak zgłaszać wyniki dwuczynnikowej analizy ANOVA