Quasi odchylenie standardowe
W tym artykule wyjaśniono, czym jest odchylenie quasi-standardowe w statystyce i jak jest obliczane. Znajdziesz więc wzór na odchylenie quasi-standardowe, rozwiązane ćwiczenie, a dodatkowo kalkulator online umożliwiający obliczenie odchylenia quasi-standardowego dowolnego zbioru danych.
Co to jest odchylenie quasi-standardowe?
W statystyce odchylenie quasi-standardowe jest miarą rozproszenia, która wskazuje na zmienność próbki. W szczególności odchylenie quasi-standardowe jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń podzielonej przez całkowitą liczbę punktów danych minus jeden.
Symbolem odchylenia quasi-standardowego jest σ n-1 os n-1 .
Odchylenie quasi-standardowe można również nazwać odchyleniem quasi-standardowym i czasami nazywane jest także odchyleniem standardowym próbki, ponieważ zwykle oblicza się je na podstawie wartości z próby statystycznej. Poniżej szczegółowo omówimy różnicę między odchyleniem quasi-standardowym a odchyleniem standardowym.
Wzór na odchylenie quasi-standardowe
Quasi-odchylenie standardowe jest równe pierwiastkowi kwadratowemu z sumy kwadratów odchyleń serii danych podzielonej przez całkowitą liczbę obserwacji minus jeden. Zatem wzór na obliczenie odchylenia quasi-standardowego jest następujący:

Złoto:
-
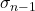
Jest to odchylenie quasi-standardowe.
-

jest wartością danych

.
-

to całkowita liczba danych.
-

jest średnią zbioru danych.
👉 Za pomocą poniższego kalkulatora możesz obliczyć odchylenie quasi-standardowe dla dowolnego zbioru danych.
Przykład obliczenia odchylenia quasi-standardowego
Biorąc pod uwagę definicję odchylenia quasi-standardowego, poniżej można zobaczyć prosty przykład obliczenia quasi-odchylenia standardowego zbioru danych.
- Budżet firmy przeznaczony na dział badawczo-rozwojowy jest bardzo zmienny, ponieważ zależy od zysku ekonomicznego, jaki firma osiągnęła w roku poprzednim. Tym samym budżet tej sekcji na przestrzeni ostatnich pięciu lat wynosił: 3, 6, 2, 9, 4 mln euro. Oblicz odchylenie quasi-standardowe tej serii danych.
Pierwszą rzeczą, którą musimy zrobić, aby wyznaczyć odchylenie quasi-standardowe, jest obliczenie średniej arytmetycznej próbki. Aby to zrobić, sumujemy wszystkie dane i dzielimy przez całkowitą liczbę obserwacji, która wynosi pięć:
![]()
Następnie stosujemy wzór na odchylenie quasi-standardowe:
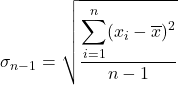
Podstawiamy dane do wzoru:
![]()
Na koniec obliczamy odchylenie quasi-standardowe:
![Rendered by QuickLaTeX.com \begin{aligned}\displaystyle\sigma_{n-1} & = \sqrt{\frac{(-1,8)^2+1,2^2+(-2,8)^2+4,2^2+(-0,8)^2}{5-1}}\\[2ex]&=\sqrt{\frac{3,24+1,44+7,84+17,64+0,64}{4}}\\[2ex]&= \sqrt{\frac{30,8}{4}}=\sqrt{7,7}=2,77 \end{aligned}](https://statorials.org/wp-content/ql-cache/quicklatex.com-cdc4009f508347a23cacbf71c71c98cc_l3.png)
Krótko mówiąc, quasi odchylenie standardowe próbki danych wynosi 2,77 miliona.
Kalkulator odchylenia quasi-standardowego
Podłącz zestaw danych statystycznych do poniższego kalkulatora online, aby obliczyć jego odchylenie quasi-standardowe. Dane należy oddzielić spacją i wprowadzić z użyciem kropki jako separatora dziesiętnego.
Quasi-odchylenie standardowe i odchylenie standardowe
Na koniec zobaczymy, jaka jest różnica między odchyleniem quasi-standardowym a odchyleniem standardowym, ponieważ są to dwie różne miary statystyczne, które mają bardzo podobną nazwę i są obliczane w bardzo podobny sposób.
Różnica między odchyleniem quasi-standardowym a odchyleniem standardowym jest mianownikiem wzoru. Aby obliczyć odchylenie quasi-standardowe, należy podzielić przez n-1, ale odchylenie standardowe oblicza się, dzieląc przez n.
Dlatego też odchylenie quasi-standardowe i odchylenie standardowe są powiązane matematycznie, ponieważ odchylenie standardowe jest równoważne odchyleniu standardowemu razy pierwiastek kwadratowy z n (całkowita liczba punktów danych) przez n-1.
![]()
Z poprzedniego równania można wywnioskować, że dla tego samego zbioru danych wartość odchylenia quasi-standardowego będzie zawsze większa od wartości odchylenia standardowego.
Ponadto do obliczenia odchylenia standardowego próbki często stosuje się wzór na odchylenie standardowe, ponieważ eliminuje to błąd systematyczne. Quasi odchylenie standardowe jest zatem dobrym estymatorem odchylenia standardowego populacji. Dlatego też, wyciągając wnioski statystyczne z próby, dość często mówi się, że oblicza się odchylenie standardowe, podczas gdy w rzeczywistości oblicza się odchylenie quasi-standardowe.